matlab练习程序(解西尔维斯特、李雅普诺夫方程)
西尔维斯特方程的形式:AX+XB=C
李雅普诺夫方程的形式:AX+XA'=-C
这两种方程都是已知矩阵A,B,C,求解X的方程。
对于这种方程有两种方法来求解,一种是朴素法,一种是Bartels-Stewart法。
以西尔维斯特方程为例,朴素法是将方程写为下列形式进行直接求解:
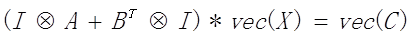
其中圆圈中带个X的符号是kron积,vec()是将X或C转换为了n*1的列向量。
该方法将原来O(n^3)的问题变为了O(n^6),如果矩阵比较大,估计速度会比较慢。
第二种方法为Bartels-Stewart法,下面以西尔维斯特方程为例介绍一下:
首先我们对A和B‘进行shur分解:
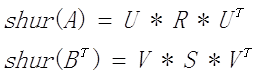
原方程可改写为:

此时令:

得到:

此时R和S都是一个上三角矩阵,我们需要S作为下三角矩阵才能方便求解。
这里的S正好是我们是对B'的shur分解,由于shur分解的特性,shur(B)=VSV',shur(B')=VS'V',所以这里再对S求个转置即可。
得到类似下面的矩阵方程:
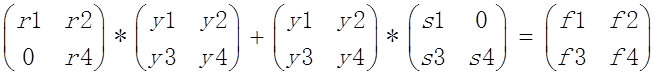
展开得到:
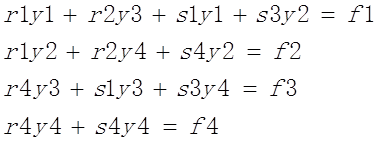
再依次求出y4,y3,y2,y1即可。
matlab代码如下:
解西尔维斯特方程:
clear all;close all;clc; A = rand(2,2); X = rand(2,2); B = rand(2,2); C = A*X+X*B; X %%系统函数 X = sylvester(A,B,C) %%朴素法,自写kron积 IA = [A zeros(2);zeros(2) A]; BI = [B(1,1)*eye(2) B(2,1)*eye(2); B(1,2)*eye(2) B(2,2)*eye(2)]; X = reshape(inv(IA+BI)*C(:),[2,2]) %%朴素法,系统kron积 X = reshape(inv(kron(eye(2),A)+kron(B',eye(2)))*C(:),[2,2]) %%Bartels–Stewart法 [U,R] = schur(A); %schur分解,R是上三角 [V,S] = schur(B'); S = S'; %S是下三角 F = U'*C*V; %解R*Y + Y*S = F方程 Y = zeros(2,2); Y(2,2) = F(2,2)/(R(2,2) + S(2,2)); Y(2,1) = (F(2,1) - S(2,1)*Y(2,2)) / (S(1,1) + R(2,2)); Y(1,2) = (F(1,2) - R(1,2)*Y(2,2)) / (R(1,1) + S(2,2)); Y(1,1) = (F(1,1) - R(1,2)*Y(2,1) - S(2,1)*Y(1,2)) / (R(1,1) + S(1,1)); X = U*Y*V'
解李雅普诺夫方程:
clear all;close all;clc; A = rand(2); X = rand(2); C = -(A*X+X*A'); X %%系统函数 X = lyap(A,C) %%朴素法,自写kron积 IA = [A zeros(2);zeros(2) A]; BI = [A(1,1)*eye(2) A(1,2)*eye(2); A(2,1)*eye(2) A(2,2)*eye(2)]; X = reshape(inv(IA+BI)*(-C(:)),[2,2]) %%朴素法,系统kron积 X = reshape(inv(kron(eye(2),A)+kron(A,eye(2)))*(-C(:)),[2,2]) %%Bartels–Stewart法 [U,R] = schur(A); %schur分解,R是上三角 S = R'; %S是下三角 F = U'*(-C)*U; %解R*Y + Y*S = F方程 Y = zeros(2,2); Y(2,2) = F(2,2)/(R(2,2) + S(2,2)); Y(2,1) = (F(2,1) - S(2,1)*Y(2,2)) / (S(1,1) + R(2,2)); Y(1,2) = (F(1,2) - R(1,2)*Y(2,2)) / (R(1,1) + S(2,2)); Y(1,1) = (F(1,1) - R(1,2)*Y(2,1) - S(2,1)*Y(1,2)) / (R(1,1) + S(1,1)); X = U*Y*U'



