matlab练习程序（差分法解二维热传导方程）

上一篇实现了一维热传导方程数值解，这一篇实现二维热传导方程数值解。

套路是一样的，先列微分方程，再改为差分方程，然后递推求解，不同的是一维热传导需要三维显示，而二维热传导需要四维，因此最后做了个三维动态图。

二维热传导方程如下：

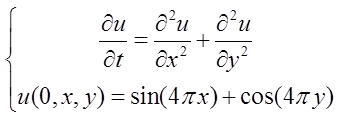
另外四条边界都是0。

写成差分方程为：

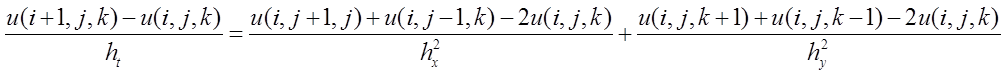
整理一下就能得到u(i+1,j,k)。

matlab代码如下：

clear all;close all;clc;

t = 0.03;       %时间范围，计算到0.03秒
x = 1;y = 1;    %空间范围，0-1米
m = 320;        %时间t方向分320个格子
n = 32;         %空间x方向分32个格子
k = 32;         %空间y方向分32个格子
ht = t/(m-1);   %时间步长dt
hx = x/(n-1);   %空间步长dx
hy = y/(k-1);   %空间步长dy

u = zeros(m,n,k);

%设置边界
[x,y] = meshgrid(0:hx:1,0:hy:1);
u(1,:,:) = sin(4*pi*x)+cos(4*pi*y);

%按照公式进行差分
for ii=1:m-1
    for jj=2:n-1
        for kk=2:k-1
            u(ii+1,jj,kk) = ht*(u(ii,jj+1,kk)+u(ii,jj-1,kk)-2*u(ii,jj,kk))/hx^2 + ...
                ht*(u(ii,jj,kk+1)+u(ii,jj,kk-1)-2*u(ii,jj,kk))/hy^2 + u(ii,jj,kk);
        end
    end
end

for i=1:200
    figure(1);
    mesh(x,y,reshape(u(i,:,:),[n k]));
    axis([0 1 0 1 -2 2]);
    
%     F=getframe(gcf);
%     I=frame2im(F);
%     [I,map]=rgb2ind(I,256); 
%     if i == 1
%         imwrite(I,map,'test.gif','gif','Loopcount',inf,'DelayTime',0.05);
%     else
%         imwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.05);    
%     end
end

结果如下：

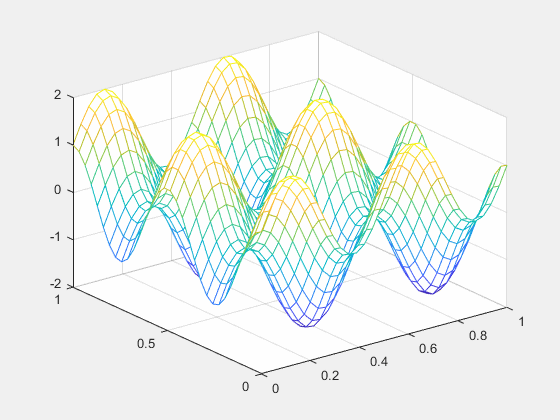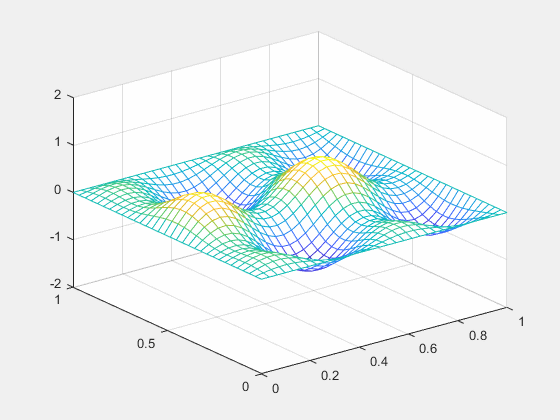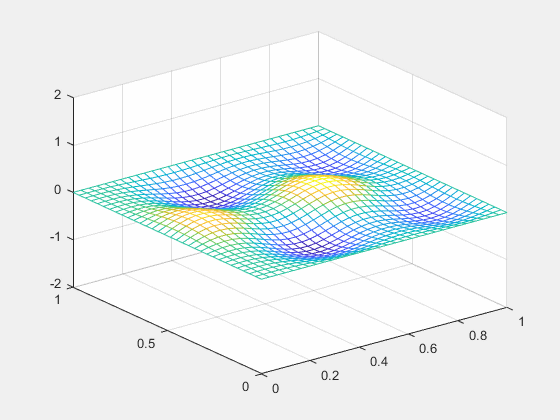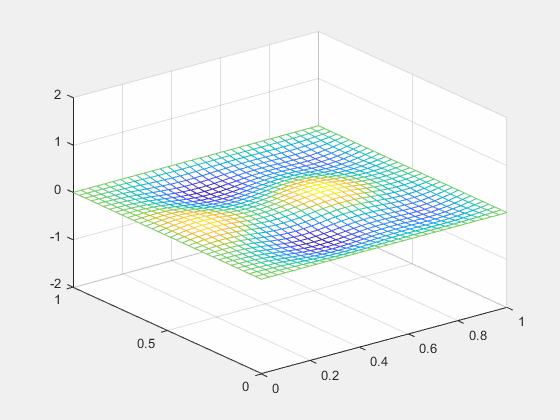
三维热传导用差分法也可以解，不过不太容易可视化，就不再实现了。