matlab练习程序（线性常微分方程组参数拟合）

比如我们已经有了微分方程模型和相关数据，如何求模型的参数。

这里以SEIR模型为例子，SEIR模型可以参考之前的文章。

一般的线性方程我们可以用最小二乘来解，一般的非线性方程我们可以用LM来解。

这里是线性微分方程组，所以我们采用最小二乘来解。

关键是构造出最小二乘形式，微分可以通过前后数据差分的方法来求。

不过这里还有一个技巧就是如果数据前后帧间隔过大，可以先插值，再对插值后的数据差分。

如果实际测量数据抖动过大导致插值后差分明显不能反映实际情况，可以先对数据平滑（拟合或是平均）再求差分。

先看SEIR微分方程：

写成矩阵形式：

 

到这里就能用最小二乘来求解了。 

matlab代码如下：

main.m：

clear all;close all;clc;

%%SEIR模型
A = [0.5 0.1 0.05 0.02];
[t,h] = ode45(@(t,x)SEIR(t,x,A),[0 300],[0.01 0.98 0.01 0]);  %[初始感染人口占比 初始健康人口占比 初始潜伏人口占比 初始治愈人口占比]
plot(t,h(:,1),'r');
hold on;
plot(t,h(:,2),'b');
plot(t,h(:,3),'m');
plot(t,h(:,4),'g');
legend('感染人口占比I','健康人口占比S','潜伏人口占比E','治愈人口占比R');
title('SEIR模型')

data=[t h];
data = data(1:3:80,:);      %间隔取一部分数据用来拟合
figure;
plot(data(:,1),data(:,2),'ro');
hold on;
plot(data(:,1),data(:,3),'bo');
plot(data(:,1),data(:,4),'mo');
plot(data(:,1),data(:,5),'go');

T=min(data(:,1)):0.1:max(data(:,1));        %插值处理，如果数据多，也可以不插值
I=spline(data(:,1),data(:,2),T)';
S=spline(data(:,1),data(:,3),T)';
E=spline(data(:,1),data(:,4),T)';
R=spline(data(:,1),data(:,5),T)';

plot(T,I,'r.');plot(T,S,'b.');
plot(T,E,'m.');plot(T,R,'g.');

%求微分，如果数据帧间导数变化太大，可以先平均或者拟合估计一个导数
%因为前面T是以0.1为步长，这里乘以10
dI = diff(I)*10; dI=[dI;dI(end)];       
dS = diff(S)*10; dS=[dS;dS(end)];
dE = diff(E)*10; dE=[dE;dE(end)];
dR = diff(R)*10; dR=[dR;dR(end)];

X = [zeros(length(I),1) -I.*S zeros(length(I),2);   %构造线性最小二乘方程组形式
     -E I.*S -E zeros(length(I),1);
     E zeros(length(I),2) -I;
     zeros(length(I),2) E I];
Y = [dS;dE;dI;dR];

A = inv(X'*X)*X'*Y

%用估计参数代入模型
[t,h] = ode45(@(t,x)SEIR(t,x,A),[0 300],[I(1) S(1) E(1) R(1)]);  %[初始感染人口占比 初始健康人口占比 初始潜伏人口占比 初始治愈人口占比]
plot(t,h(:,1),'r');
hold on;
plot(t,h(:,2),'b');
plot(t,h(:,3),'m');
plot(t,h(:,4),'g');

SEIR.m：

function dy=SEIR(t,x,A)
alpha = A(1);        %潜伏期转阳率
beta = A(2);         %感染率
gamma1 = A(3);      %潜伏期治愈率
gamma2 = A(4);      %患者治愈率
dy=[alpha*x(3) - gamma2*x(1);
    -beta*x(1)*x(2);
    beta*x(1)*x(2) - (alpha+gamma1)*x(3);
    gamma1*x(3)+gamma2*x(1)];

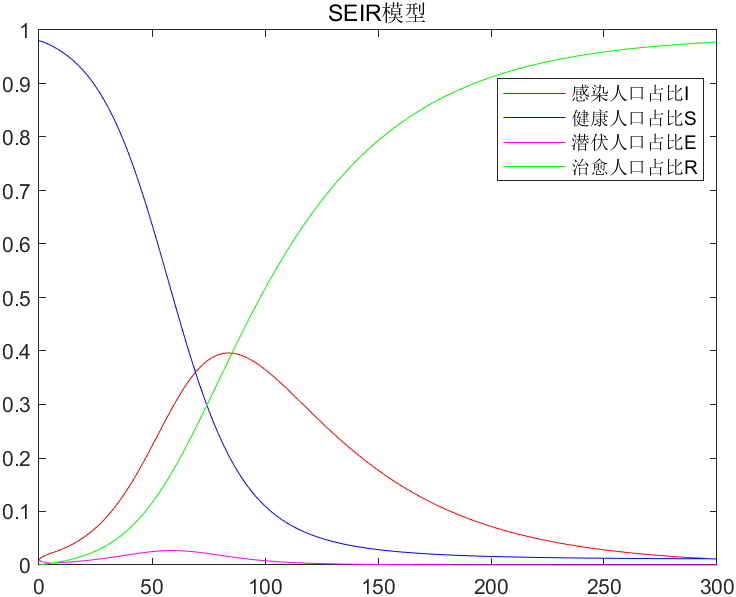
结果：

原始参数[0.5 0.1 0.05 0.02]与模型：

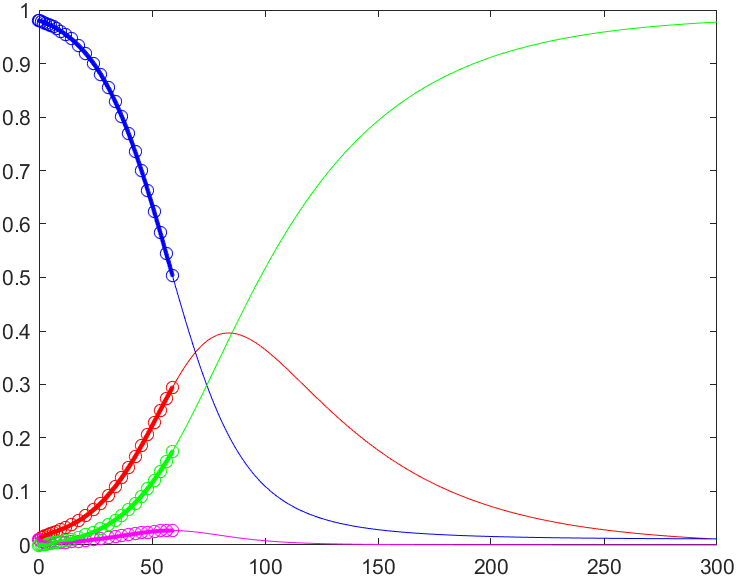
拟合参数[0.499921929359668 0.100099242849855 0.0505821757746970 0.0199739921888752]与模型：