matlab练习程序（空间椭圆拟合）

之前实现过三维椭圆拟合，当时是利用已知点先进行椭球拟合，再进行平面拟合，通过解两个面的相交线得到空间椭圆函数。

如果只知道空间坐标可以用上述的方法，但是通常我们获得空间点时会附带时间信息，因此我们可以认为三个分量都是时间的函数，来进行拟合。

函数如下：

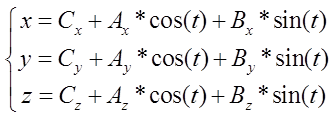
由于是非线性方程组，下面我们只需要用高斯牛顿法或者LM法计算非线性最小二乘就可以了。

代码如下：

clear all;
close all;
clc;

warning off;
A = rand(1,3);
B = rand(1,3);
C = rand(1,3);

t = 0:0.01:2*pi;
p=[];
for i=1:length(t)
    x =  C(1) + A(1)*cos(t(i)) + B(1)*sin(t(i));
    y =  C(2) + A(2)*cos(t(i)) + B(2)*sin(t(i));
    z =  C(3) + A(3)*cos(t(i)) + B(3)*sin(t(i));
    p=[p;x y z];
end

selectnum = 50;
ind = randperm(length(p),selectnum);   
t = t(ind)';
data = p(ind,:) + (rand(selectnum,3)-0.5)/10;

plot3(p(:,1),p(:,2),p(:,3),'.');
grid on;
hold on;
plot3(data(:,1),data(:,2),data(:,3),'r*');

X = data(:,1);
Y = data(:,2);
Z = data(:,3);

prex = rand(3,1);
prey = rand(3,1);
prez = rand(3,1);
for i=1:500
    
    Fx = prex(1) + prex(2)*cos(t) + prex(3)*sin(t);
    Fy = prey(1) + prey(2)*cos(t) + prey(3)*sin(t);
    Fz = prez(1) + prez(2)*cos(t) + prez(3)*sin(t);
    
    Gx = X - Fx;
    Gy = Y - Fy;
    Gz = Z - Fz;
    
    Dc = ones(length(t),1);
    Da = cos(t);
    Db = sin(t);
    J = [Dc Da Db];
    
    deltax = inv(J'*J)*J'* Gx;
    deltay = inv(J'*J)*J'* Gy;
    deltaz = inv(J'*J)*J'* Gz;
    
    pcurx = prex+deltax;
    pcury = prey+deltay;
    pcurz = prez+deltaz;
    
    prex = pcurx;
    prey = pcury;
    prez = pcurz;
end

t = 0:0.01:2*pi;
p=[];
for i=1:length(t)
    x =  prex(1) + prex(2)*cos(t(i)) + prex(3)*sin(t(i));
    y =  prey(1) + prey(2)*cos(t(i)) + prey(3)*sin(t(i));
    z =  prez(1) + prez(2)*cos(t(i)) + prez(3)*sin(t(i));
    p=[p;x y z];
end

plot3(p(:,1),p(:,2),p(:,3),'go');

拟合结果：

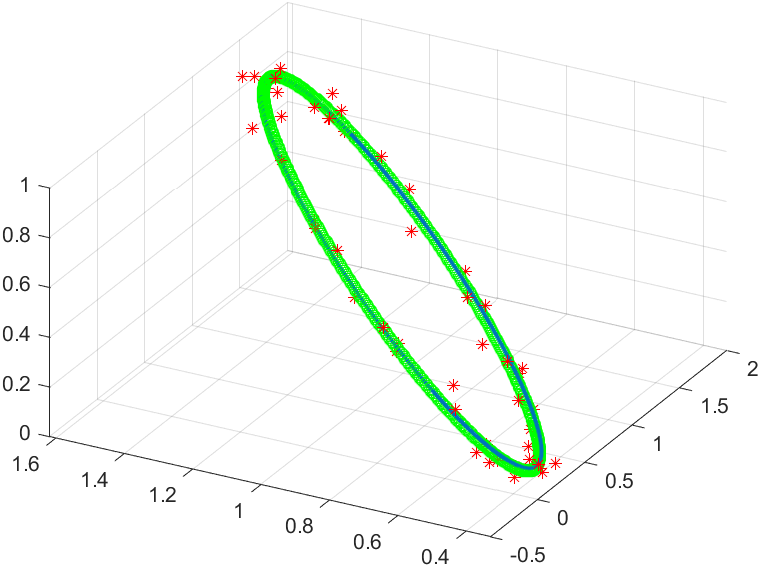
蓝色点为原始椭圆。

红色星为蓝色点中选50个点并且加入噪声后的点。

绿色圈为拟合结果。