matlab练习程序（罗德里格斯变换）

给出空间中一个点，将该点绕向量(k1 k2 k3)旋转一定角度theta，从而得到新点，这种操作能够利用罗德里格斯变换来处理。

变换公式如下：

其中theta为旋转度数。

K为由点所绕的单位向量构成的矩阵。

比如所绕向量为(k1 k2 k3)，则矩阵K表示如下：

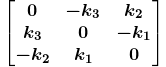
公式中R即为进行这种变换的旋转矩阵。

同样，用四元数也能够完成这种旋转操作。

下面给出了用四元数和罗德里格斯变换对同一个点做旋转的例子，互相验证一下。

matlab代码如下：

clear all;
close all;
clc;

p=rand(1,3);        %待旋转点

quat = eul2quat([0.6,0.4,0.5]);     %利用欧拉角构造四元数
q_quat = quaternion(quat);
p_quat = quaternion([0 p]);
re_quat= q_quat*p_quat*q_quat';     %利用四元数旋转
[w,a,b,c] = parts(re_quat);         %得到四元数中四个数

theta = acos(quat(1))*2;            %得到旋转弧度和所环绕的向量
kx = quat(2)/sin(theta/2);
ky = quat(3)/sin(theta/2);
kz = quat(4)/sin(theta/2);

K=[0 -kz ky;
   kz 0 -kx;
   -ky kx 0];
R = eye(3) + sin(theta)*K + (1- cos(theta))*K*K;    %罗德里格斯公式
p1= R*p';                           %利用罗德里格斯公式计算的旋转后的点

dr = HelperDrawRotation;
figure;
dr.draw3DOrientation(gca,[quat(2:4)],theta*180/pi);

hold on;
plot3(p(1),p(2),p(3),'bo')
plot3(p1(1),p1(2),p1(3),'r*')
plot3(a,b,c,'go');
axis equal;

其中的HelperDrawRotation是matlab帮助中的例子，我就不贴了，可以点击这里下载。

变换效果如下：

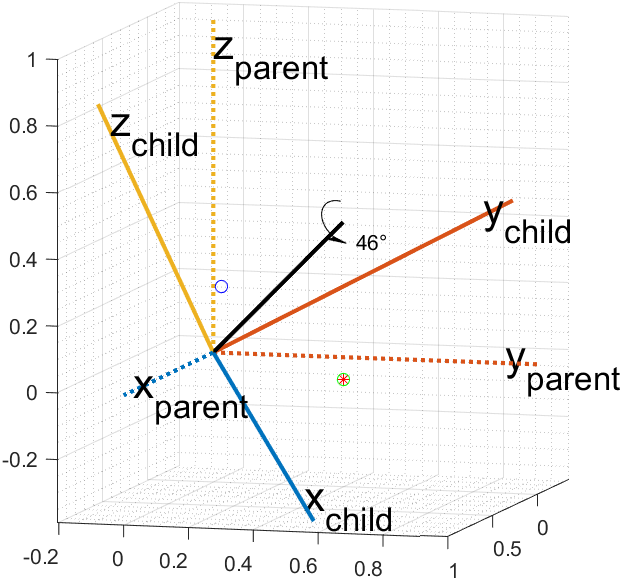
利用四元数和罗德里格斯变换将蓝圈变换到绿圈(红星)上，结果是一致的。

注：这里matlab版本为2019a，2018a之前版本可能没有quaternion这个函数。