matlab练习程序（多边形扩展算法）

这里提供两种思路：

一、基于顶点的扩展

1. 确定扩展距离dis。

2. 计算每个顶点相邻边的单位向量。

3. 确定扩展方向，判断依据是相邻边向量的行列式的正负号，记为sign(sina)。

4. 计算顶点相邻两边的单位向量和，得到新向量，再对新向量进行单位化得到v。

5. 对每个顶点加上对应的sign(sina)*dis*v即可。

不过这种方法我发现最终扩展的多边形和原多边形的形状有微小区别。

因为新多边形和原多边形的边可能不完全平行。

二、基于边的扩展

1. 确定扩展距离dis。

2. 计算边的法线向量v。

3. 确定扩展方向，判断依据是边向量和其法线向量的行列式的正负号，记为sign(sina)。

4. 对边上的两个顶点分别加上sign(sina)*dis*v得到新边的两个顶线。

5. 计算所有边的新顶点，并且根据新的顶点对计算其所在直线。

6. 计算所有直线的交点即得到新多边形的顶点。

这种方法得到的多边形每条边和原多边形的完全平行的。

matlab代码如下：

clear all;
close all;
clc;

dis = 0.1;

n=5;
p=rand(n,2);
p=createSimplyPoly(p);  %创建简单多边形

p=[p;p(1,:)];
plot(p(:,1),p(:,2),'r-o')

%%第一种方法，对每个顶点延相邻边单位向量和的反方向扩展dis距离，得到新多边形
R = [];
revR = [];
for i=1:length(p)-1             %计算每个顶点两条边的向量
    R = [R;p(i+1,:)-p(i,:)];
    if i==1
        revR =[revR;p(end-1,:)-p(1,:)];
    else
        revR =[revR;p(i-1,:)-p(i,:)];
    end
end

direct = [];
sina=[];
for i=1:length(R)               %计算顶点两条边单位向量求和并确定扩展方向
    D = R(i,:)/norm(R(i,:))+ revR(i,:)/norm(revR(i,:));
    sina = [sina;det([R(i,:);revR(i,:)])];
    direct = [direct;D/norm(D)];
end

newp = p;
newp(1:end-1,:) = p(1:end-1,:) + dis*sign(sina).*direct;
newp(end,:)=newp(1,:);

hold on;
plot(newp(:,1),newp(:,2),'b-o')
axis equal;

%%第二种方法，对每条边向外扩展dis距离，再将每条扩展边求交点得到新多边形
new_line=cell(length(p),1);
for i=1:length(p)-1             %计算多边形每条边外扩dis距离得到新边
    cur_line = p(i:i+1,:);
    k = (p(i+1,2) - p(i,2))/(p(i+1,1) - p(i,1));
    new_k  = -1/k;
    n = [1 ,new_k];
    n = n/norm(n);
    sina = det([p(i+1,:)-p(i,:);n]);
    new_line{i} = cur_line + n*sign(sina)*dis;
end

new_line{length(p)} = new_line{1};
newp2=[];
for i=1:length(p)-1             %对新边求交点得到扩展多边形
    
    line1 = new_line{i};
    line2 = new_line{i+1};
    
    k1 = (line1(2,2)-line1(1,2))/(line1(2,1) - line1(1,1));
    b1 = line1(1,2) - k1*line1(1,1);
    
    k2 = (line2(2,2)-line2(1,2))/(line2(2,1) - line2(1,1));
    b2 = line2(1,2) - k2*line2(1,1);
    
    x = (b2-b1)/(k1-k2);
    y = k1*x+b1;
    
    newp2=[newp2;x y];
end

figure;
plot(p(:,1),p(:,2),'r-o')
hold on;
newp2 =[newp2;newp2(1,:)];
plot(newp2(:,1),newp2(:,2),'b-o');
axis equal;

createSimplyPoly.m：

function p=createSimplyPoly(p)
    cen=mean(p);
    ang=atan2(p(:,1)-cen(1),p(:,2)-cen(2)); %每个点到坐标中心极角

    p=[p,ang];
    p=sortrows(p,3);    %按极角排序

    p=p(:,1:2);
end

第一种方法：

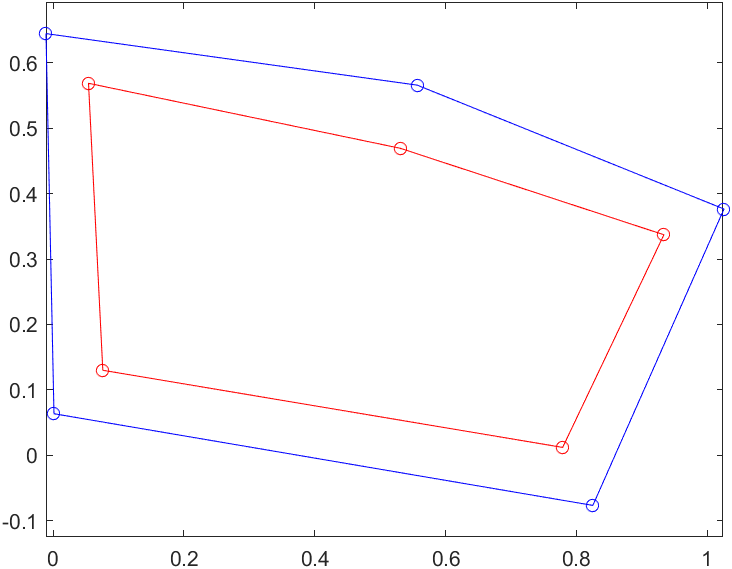
第二种方法：

 第二种方法从生成图形的形状上看会好看些。