matlab练习程序(EM算法)
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
最大期望算法经过两个步骤交替进行计算:
第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
下面用EM算法对高斯混合模型进行聚类,该算法不仅能够给出聚类后数据的均值,还能够给出协方差。
代码如下:
clear all; close all; clc; mu1=[0 0]; S1=[0.8 0.1]; data1=mvnrnd(mu1,S1,1000); plot(data1(:,1),data1(:,2),'r.'); hold on; mu2=[2 4]; S2=[0.4 1.3]; data2=mvnrnd(mu2,S2,1000); plot(data2(:,1),data2(:,2),'g.'); mu3=[-2 3]; S3=[2.4 1.3]; data3=mvnrnd(mu3,S3,1000); plot(data3(:,1),data3(:,2),'b.'); %利用EM算法对高斯混合模型聚类 data=[data1;data2;data3]; mu{1} = rand(1,2); mu{2} = rand(1,2); mu{3} = rand(1,2); sigma{1} = rand(1,2); sigma{2} = rand(1,2); sigma{3} = rand(1,2); p = [0.3 0.4 0.4]; w=zeros(length(data),3); for i=1:1000 %E-step for j=1:3 w(:,j) = p(j)*mvnpdf(data,mu{j},sigma{j}); end w = w./repmat(sum(w,2),[1 3]); %M-step for j=1:3 mu{j} = w(:,j)'* data / sum(w(:,j)); sigma{j} = sqrt(w(:,j)'*((data-mu{j}).*(data-mu{j})) / sum(w(:,j))); end p = sum(w) / length(data); end figure; w = uint8(w); data1 = data(w(:,1)==1,:); data2 = data(w(:,2)==1,:); data3 = data(w(:,3)==1,:); plot(data1(:,1),data1(:,2),'r.'); hold on; plot(data2(:,1),data2(:,2),'g.'); plot(data3(:,1),data3(:,2),'b.');
结果:
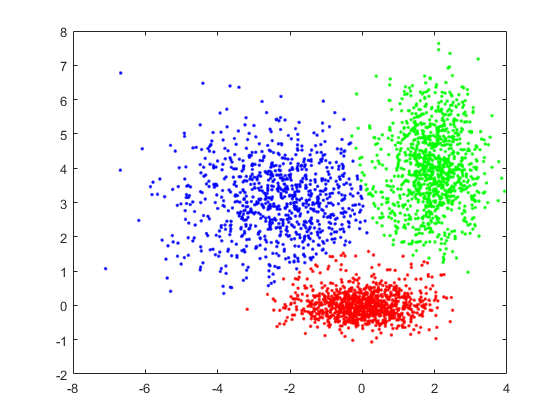
原始高斯数据:
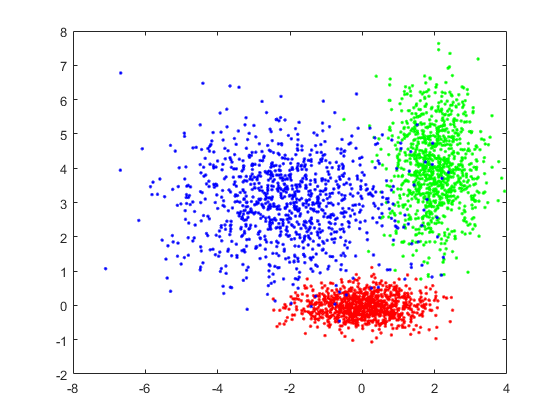
聚类后: