matlab练习程序（IFS分形）

IFS为迭代函数系统，是一种构造分形的方法。

方法的核心是以概率p的方式对初始点进行仿射平移变换。

变换公式为：

x(k+1)=a*x(k) + b*y(k) + e
y(k+1)=c*x(k) + d*y(k) + f

关键是确定IFS码表，只要码表确定了，后面的编程套路基本一样。

下面列两个常见的码表及分形效果。

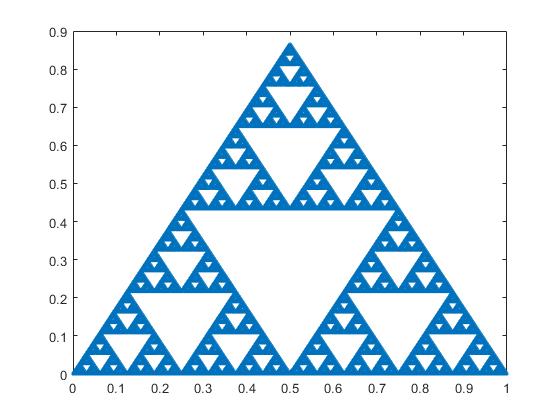
Sierpinski垫IFS码表：

w	a	b	c	d	e	f	p
1	0.5	0	0	0.5	0	0	0.333
2	0.5	0	0	0.5	0.25	0.433	0.333
3	0.5	0	0	0.5	0.5	0	0.333

matlab代码如下：

clear all;
close all;
clc;

n=500000;
x=zeros(n,1);
y=zeros(n,1);
for k=2:n
    p=rand(1);
    if p < 0.33
        x(k)=0.5*x(k-1)+0*y(k-1);
        y(k)=0*x(k-1)+0.5*y(k-1);
    elseif p< 0.66
        x(k)=0.5*x(k-1)+0*y(k-1)+0.25;
        y(k)=0*x(k-1)+0.5*y(k-1)+0.433;
    else
        x(k)=0.5*x(k-1)+0*y(k-1)+0.5;
        y(k)=0*x(k-1)+0.5*y(k-1);
    end
end

plot(x,y,'.')

效果：

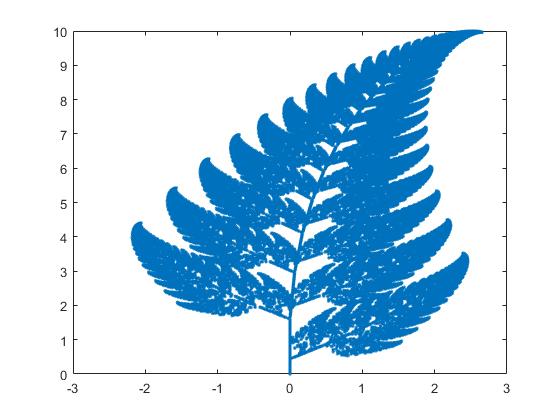
Barnsley羊齿叶IFS码表：

w	a	b	c	d	e	f	p
1	0	0	0	0.16	0	0	0.01
2	0.85	0.04	-0.04	0.85	0	1.6	0.85
3	0.2	-0.26	0.23	0.22	0	1.6	0.07
4	-0.15	0.28	0.26	0.24	0	0.44	0.07

matlab代码如下：

clear all;
close all;
clc;

n=100000;
x=zeros(n,1);
y=zeros(n,1);
for k=2:n
    p=rand(1);
    if p < 0.01
        y(k)=0.16*y(k-1);
    elseif p < 0.86
        x(k)=0.85*x(k-1)+0.04*y(k-1);
        y(k)=-0.04*x(k-1)+0.85*y(k-1)+1.6;
    elseif p < 0.93
        x(k)=0.2*x(k-1)-0.26*y(k-1);
        y(k)=0.23*x(k-1)+0.22*y(k-1)+1.6;
    else
        x(k)=-0.15*x(k-1)+0.28*y(k-1);
        y(k)=0.26*x(k-1)+0.24*y(k-1)+0.44;        
    end
end

plot(x,y,'.');

效果：

如何构造IFS码表是一个难点，有码表后生成分形其实是比较简单的。