matlab练习程序（常微分方程向量场）

通过向量场能很直观的看到微分方程所有解的变化规律。

这里随便设了个方程：dx/dt = sin(t)*cos(x)+sin(t)。

由于方程本身就代表了x在t处的斜率，所以：

vt = cos(atan(f));

vx = sin(atan(f));

matlab代码如下：

clear all;
close all;
clc;

t = -5:0.3:5;
x = -5:0.3:5;

f = @(t,x) sin(t).*cos(x)+sin(t);

[t,x] = meshgrid(t,x);

vt = cos(atan(f(t,x)));
vx = sin(atan(f(t,x)));

quiver(t,x,vt,vx);

hold on
[t,x] = ode45(f,[-5 5],[3;-2;-4]);
plot(t,x,'r');

结果如下：

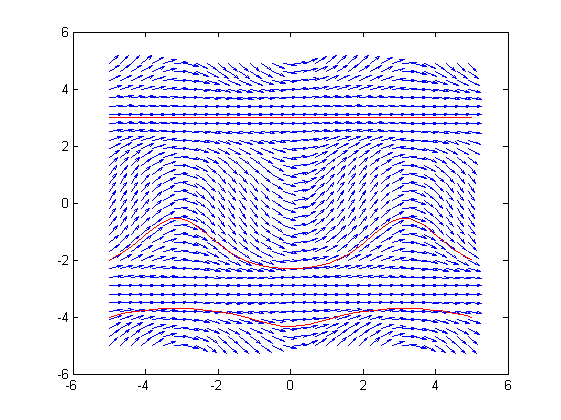
红线为微分方程的三个特解。

关于方程组的向量场绘制可以参考这里。