matlab练习程序（人工势场法）

该方法也是一种路径规划算法，不过障碍物过多的时候建立势场可能比较耗时，而且容易陷入局部最优。

算法流程如下：

1. 对于栅格场景中每一个像素分别计算到终点的距离，距离越大，则对该像素赋值越大，结束得到引力场。

2. 对于栅格场景中每一个像素分别计算到所有障碍物的距离，距离越大，则对该像素赋值越小，结束得到斥力场。

3. 引力场和斥力场相加得到总人工势场。

4. 得到人工势场后，从起始位置用梯度下降或者邻域搜索法找到一条路径到结束点。

这里建立势场只用到了障碍物最外层边界，如果障碍物所有像素全部用来计算，太过于耗时了。路径寻找用了邻域搜索。

matlab代码如下：

clear all;
close all;
clc;

img = imread('map.png');
imshow(img);
[h,w] = size(img);

img1 = 255-(img-imerode(img,ones(3)));  %求边界
figure;
imshow(img1);

p = ginput();
hold on;
plot(p(:,1),p(:,2),'r.')

grav = zeros(h*w,1);                    %引力场
repu = zeros(h*w,1);                    %斥力场

ind=zeros(h*w,2);
indobs=zeros(sum(sum((255-img1)>0)),2);
num = 1;
for i=1:h
    for j=1:w
        ind((i-1)*w+j,:) = [j i];
        if img1(i,j) ==0   
            indobs(num,:)=[j i];
            num = num + 1;
        end
        d = norm([j,i]-p(2,:));             %根据距离判断，距离越小，值越小
        grav((i-1)*w+j) = 2*d;              %建立引力场,2是引力系数
    end
end

for i=1:length(indobs)
    t = ind - repmat(indobs(i,:),length(ind),1);    %根据距离判断，距离越小，值越大
    repu = repu + 5./sqrt(t(:,1).^2+t(:,2).^2);       %建立斥力场,5是斥力系数
end

repu(repu>500) = 500;
re = grav + repu;                           %综合场

imgre = reshape(re,[h,w])';

nei=[ -1 -1; -1 0; -1 1;
       0 -1; 0 0;  0 1;
       1 -1; 1 0;  1 1];
path=floor(p(1,:));
pre = [0 0];
while norm(path(end,:)-p(2,:))>2    
    pc = path(end,:);
    im = imgre(pc(end,2)-1:pc(end,2)+1,pc(end,1)-1:pc(end,1)+1);
    [~,ind] = min(reshape(im,9,1));         %八邻域找最小值
    
    pre = path(end,:);   
    path = [path;path(end,:)+nei(ind,:)];
    
    if  norm(path(end,:)-pre) == 0 || ...           %超出边界或陷入局部最优了
        path(end,1)==1 || path(end,2) ==1 || ...
        path(end,1)==w || path(end,2) ==h;
        break;
    end
end

hold on;
plot(path(:,1),path(:,2));
figure;
mesh(imgre);

结果如下：

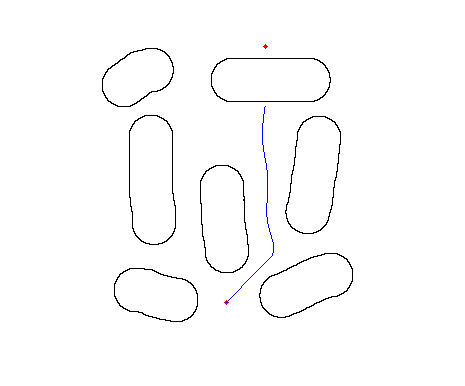
原图：

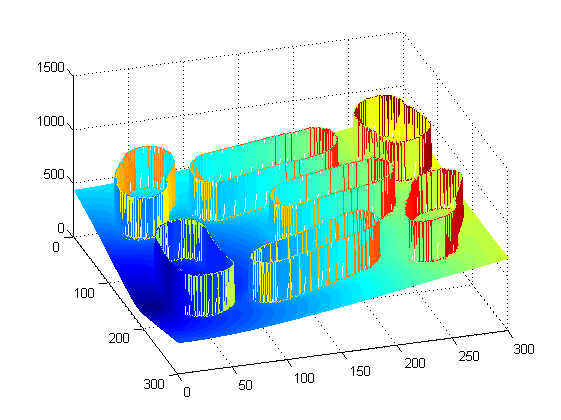
人工势场：

规划路径：

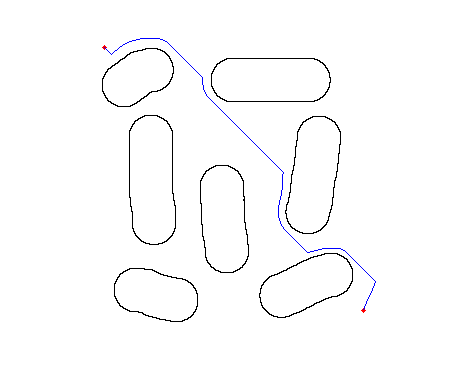
不过该方法有时候会陷入局部最优，比如下面这个势场：

规划路径：