matlab练习程序（柏林噪声）

关于噪声生成，我们可以使用rand(256)这样的函数生成256*256大小的随机噪声，这样的噪声我们称为白噪声。

不过白噪声过于随机，有时候并不能反映真实的噪声，比如山丘，纹理等不那么“随机”的起伏。

因此有人开发了柏林噪声，该噪声在图形学中的地形，云彩或火焰生成等方法中经常使用。

下面介绍下算法过程：

1. 首先定义网格大小和待生成图像的大小。

2. 对网格每一个顶点生成随机方向向量，就是下图红色的向量。

3. 遍历图像每一个像素，计算该像素到该像素所在网格四个顶点组成的向量d，就是下图右边蓝色的向量。

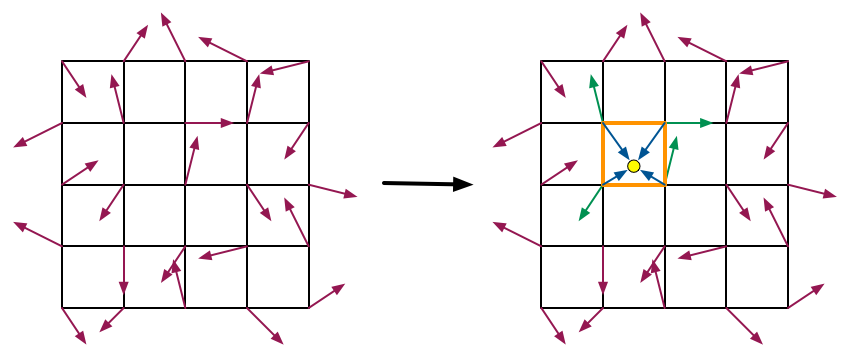
4. 计算网格顶点随机方向向量与3中求得的向量d的点积，得到方向权重。

5. 利用平滑函数对dx、dy平滑，得到比例系数sx、sy。平滑函数要符合f(0) = 0，f(0.5)=0.5，f(1)=1的方程，最好满足二阶导数连续。

6. 根据方向权重与平滑函数得到的系数对当前像素赋值。

matlab代码如下：

clear all;close all;clc;

n = 256;        %噪声图像大小
cellsize = 10;  %网格大小，不同的大小会产生不同尺度的噪声

G = rand(2,n/cellsize+2,n/cellsize+2)-0.5; %每个网格顶点的随机方向向量

img = zeros(n);
for i=1:n
    for j=1:n

        indi = i/cellsize+1;        
        indj = j/cellsize+1;
        
        floori = floor(indi);
        floorj = floor(indj);
        
        d00 = [indi indj] - [floori floorj];        %计算当前点到当前网格四个角点距离
        d10 = [indi indj] - [floori+1 floorj];
        d01 = [indi indj] - [floori floorj+1];
        d11 = [indi indj] - [floori+1 floorj+1];
        
        s = sum(G(:,floori,floorj).*d00');          %当前网格四个角点方向向量对当前点的方向权重
        t = sum(G(:,floori+1,floorj).*d10');
        u = sum(G(:,floori,floorj+1).*d01');
        v = sum(G(:,floori+1,floorj+1).*d11');
        
        dx = indi - floori;
        dy = indj - floorj;
        
        sy = 6*dy.^5-15*dy.^4+10*dy.^3;   %符合f(0) = 0,f(0.5)=0.5,f(1)=1的方程,满足二阶导数连续
        sx = 6*dx.^5-15*dx.^4+10*dx.^3;   %用于描述网格内的起伏
        
        a = s + (t-s)*sx;
        b = u + (v-u)*sx;

        img(i,j) = a + (b-a)*sy;
    end
end
imshow(img,[])

网格25生成的图像：

网格10生成的图像：

最后不同网格尺度生成的噪声也能够进行叠加，得到更多种类的噪声。

参考：

https://blog.csdn.net/candycat1992/article/details/50346469

http://www.twinklingstar.cn/2015/2581/classical-perlin-noise/