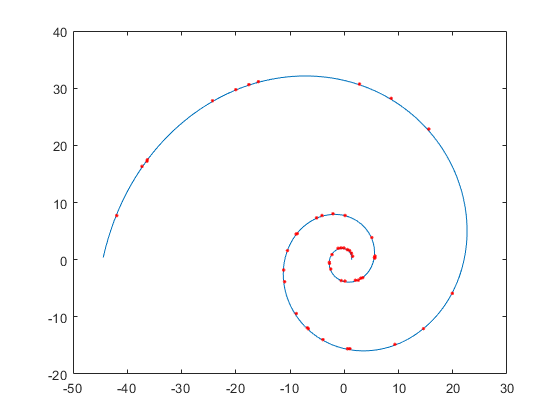
matlab练习程序(螺线拟合)
这里待拟合的螺线我们选择阿基米德螺线,对数螺线类似。
螺线的笛卡尔坐标系方程为:
螺线从笛卡尔坐标转为极坐标方程为:
阿基米德螺线在极坐标系下极径r和极角theta为线性关系,方程为:
计算步骤如下:
1.通常我们首先得到螺线在笛卡尔坐标下的一些点x,y。
2.然后根据x,y计算出r和theta。
3.最后拟合的目标就是计算出a和b,这一步可以用最小二乘。
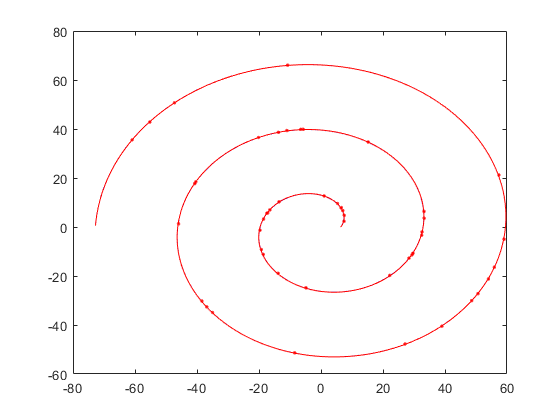
拟合结果:
下图蓝色线为原始线(这里可能看不到),红色线为拟合线,红色点为测量点。
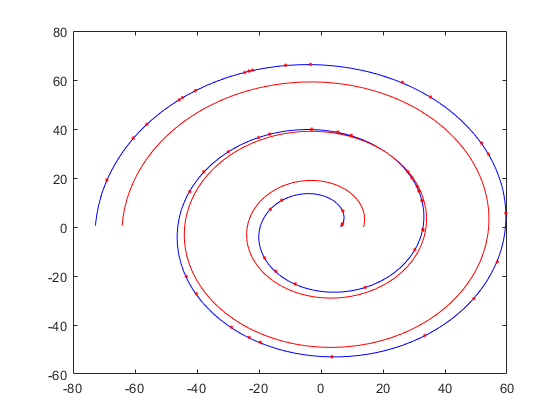
放大看一下:

不过有时候拟合也会失败(这时候就可以祭出ransac大法了):
matlab代码如下:
clear all; close all; clc; %%生成阿基米德螺线 a=6.34; b=4.23; theta=0:0.01:5*pi; r = a+b*theta; x = r.*cos(theta); y = r.*sin(theta); plot(x,y,'b') %%生成待拟合数据 ind = randperm(length(x),50); dat=[x(ind)' y(ind)'] + rand(50,2)/5; hold on; plot(dat(:,1),dat(:,2),'r.'); T = atan(dat(:,2)./dat(:,1)); R = sqrt(dat(:,1).^2+dat(:,2).^2); %%因为T是周期为pi循环数列,因此需要根据不同圈数加pi D=[R T]; D=sortrows(D); E=D; n = 0; for i=2:length(D) if D(i,2)-D(i-1,2)<0 && D(i,2)<0 n=n+1; end E(i,2) = E(i,2) + n*pi; end X = [E(:,2) ones(length(dat),1)]; Y = E(:,1); C = inv(X'*X)*X'*Y; theta=0:0.01:5*pi; r = C(2)+C(1)*theta; x = r.*cos(theta); y = r.*sin(theta); plot(x,y,'r') %%生成对数螺线 a=1.34; b=2.23; theta=0:0.01:5*pi; r = a*exp(b*theta/10); x = r.*cos(theta); y = r.*sin(theta); figure; plot(x,y) ind = randperm(length(x),50); dat=[x(ind)' y(ind)'] + rand(50,2)/5; hold on; plot(dat(:,1),dat(:,2),'r.');
最后还生成了对数螺线,大家可以自行尝试拟合一下哈。