matlab练习程序（点云表面法向量）

思路还是很容易想到的：

1.首先使用KD树寻找当前点邻域的N个点，这里取了10个，直接调用了vlfeat。

2.用最小二乘估计当前邻域点组成的平面，得到法向量。

3.根据当前邻域点平均值确定邻域质心，通常质心会在弯曲表面的内部，反方向即为法线方向。

vlfeat在这里下载，配置参考这里，rabbit.pcd下载地址

处理效果如下：

原始点云：

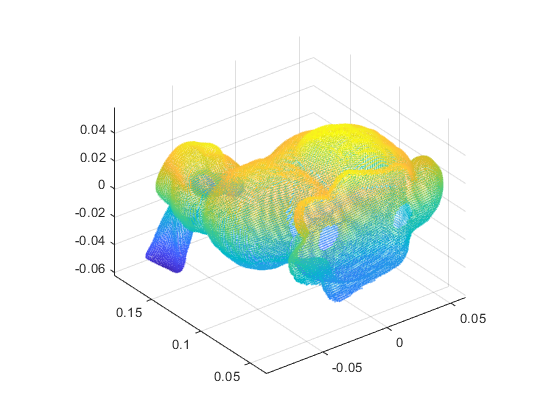
点云表面法向量，做了降采样处理：

兔子果断变刺猬。

matlab代码如下：

clear all;
close all;
clc;
warning off;

pc = pcread('rabbit.pcd');
pc=pcdownsample(pc,'random',0.3);       %0.3倍降采样
pcshow(pc);

pc_point = pc.Location';                %得到点云数据
kdtree = vl_kdtreebuild(pc_point);      %使用vlfeat建立kdtree

normE=[];
for i=1:length(pc_point)
    
    p_cur = pc_point(:,i);
    [index, distance] = vl_kdtreequery(kdtree, pc_point, p_cur, 'NumNeighbors', 10);    %寻找当前点最近的10个点
    p_neighbour = pc_point(:,index)';
    p_cent = mean(p_neighbour);     %得到局部点云平均值，便于计算法向量长度和方向
    
    %最小二乘估计平面
    X=p_neighbour(:,1);
    Y=p_neighbour(:,2);
    Z=p_neighbour(:,3);
    XX=[X Y ones(length(index),1)];
    YY=Z;
    %得到平面法向量
    C=(XX'*XX)\XX'*YY;
    
    %局部平面指向局部质心的向量
    dir1 = p_cent-p_cur';
    %局部平面法向量
    dir2=[C(1) C(2) -1];
    
    %计算两个向量的夹角
    ang = sum(dir1.*dir2) / (sqrt(dir1(1)^2 +dir2(1)^2) + sqrt(dir1(2)^2 +dir2(2)^2)+sqrt(dir1(3)^2 +dir2(3)^2) );
    
    %根据夹角判断法向量正确的指向
    flag = acos(ang);
    dis = norm(dir1);
    if flag<0
        dis = -dis;
    end
    
    %画出当前点的表面法向量
    t=(0:dis/100:dis)';
    x = p_cur(1) + C(1)*t;
    y = p_cur(2) + C(2)*t;
    z = p_cur(3) + (-1)*t;
    
    normE =[normE;x y z];
    i
end
pcshowpair(pc,pointCloud(normE));