matlab练习程序（马尔可夫聚类MCL）

本文主要参考：

https://wenku.baidu.com/view/b7907665caaedd3383c4d31b.html

https://blog.csdn.net/u010376788/article/details/50187321

虽然参考上面两篇文章，不过这里和他给出的算法步骤不完全一致。

因为上面文章是针对Graphs的，矩阵中有边为0的数据，而我的数据是Vector的，边是根据距离计算出来的，应该还是有点区别的，而且我还用了kmeans。

首先给出他的算法步骤：

　　1.输入一个无向图，Expansion的幂e和Inflation的参数r。

　　2.创建邻接矩阵。

　　3.对每个结点添加自循环（可选的）。

　　4.标准化矩阵（每个元素除以所在列的所有元素之和）。

　　5.计算矩阵的第e次幂。

　　6.用参数r对求得的矩阵进行Inflation处理。

　　7.重复第5步和第6步，直到状态稳定不变（收敛）。

　　8.把最终结果矩阵转换成聚簇。

然后是这里的算法步骤：

　　1.输入数据，创建邻接矩阵。

　　2.标准化矩阵（每个元素除以所在列的所有元素之和）。

　　3.对标准化后的矩阵进行马尔可夫状态转移。

　　4.重复第2步和第3步，直到状态稳定不变（收敛）。

　　5.使用kmeans把最终结果矩阵转换成聚簇。（不明白kmeans的可以看看这篇文章）

代码如下：

clear all;
close all;
clc;

K=3;
theta=0:0.01:2*pi;
p1=[3*cos(theta) + rand(1,length(theta))/2;3*sin(theta)+ rand(1,length(theta))/2];
p2=[2*cos(theta) + rand(1,length(theta))/2;2*sin(theta)+ rand(1,length(theta))/2];
p3=[cos(theta) + rand(1,length(theta))/2;sin(theta)+ rand(1,length(theta))/2];
p=[p1 p2 p3]';

randIndex = randperm(length(p))';       %打乱数据顺序
p=p(randIndex,:);
plot(p(:,1),p(:,2),'.')

for i = 1:length(p)
    for j =1:length(p)
        W(i,j) = sqrt(sum((p(i,:)-p(j,:)).^2));　　%根据距离初始化无向图的边
    end
end

preW=W;
while 1
    x=repmat(sum(W),length(p),1);
    W=W./x;
    W=W*W;                      %马尔科夫状态转移
    
    if sum(sum(preW-W))<1e-15
        break;
    end
    
    preW=W;
end

[idx,ctrs] = kmeans(W(:,1),K);          %用kmeans将收敛矩阵转换为聚簇
figure;
plot(p(idx==1,1),p(idx==1,2),'r.') 
hold on;
plot(p(idx==2,1),p(idx==2,2),'g.')    
plot(p(idx==3,1),p(idx==3,2),'b.') 

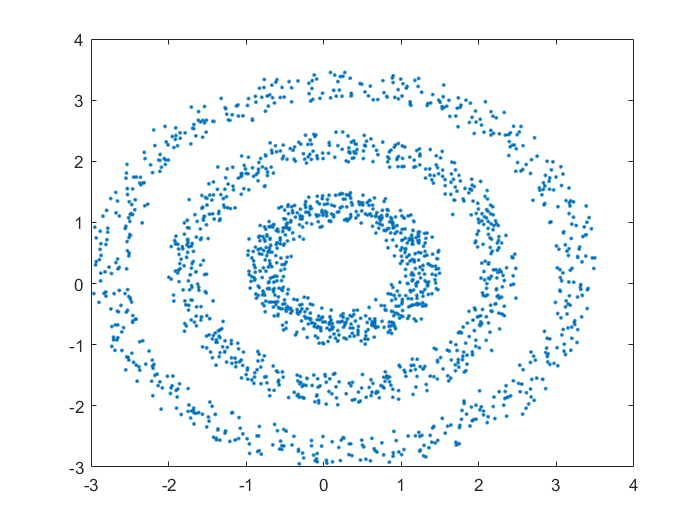
原始数据：

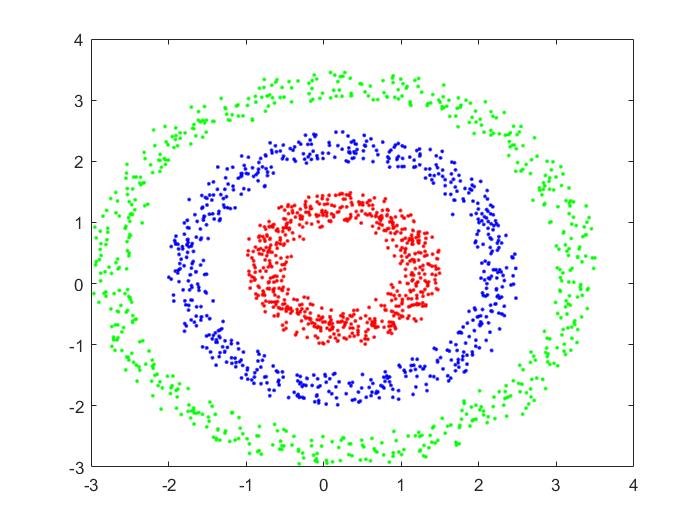
聚类后：