Acwing算法模板(自己用)
题目均可以在acwing中搜索得到
目录
基础算法
二分
整数二分模板
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000010;
int a[maxn];
int main(){
int n,q; cin>>n>>q;
for(int i=0;i<n;i++) cin>>a[i];
while(q--){
int x; cin>>x;
int l=0,r=n-1;
while(l<r){
int mid = l+r>>1;
if(a[mid]>=x) r=mid;
else l=mid+1;
}
if(a[l]!=x)cout<<"-1 -1\n";
else{
cout<<l<<" ";
l=0,r=n-1;
while(l<r){
int mid = l+r+1>>1;
if(a[mid]<=x) l=mid;
else r=mid-1;
// cout<<mid<<" "<<l<<" "<<r<<endl;
}
cout<<l<<endl;
}
}
return 0;
}
实数二分模板
//求 根号
#include<bits/stdc++.h>
using namespace std;
int main(){
double x; cin>>x;
double l=0,r=x;
while(r-l>1e-6){
double mid = (l+r)/2;
if(mid*mid>=x) r=mid;
else l=mid;
}
cout<<l;
return 0;
}
求三次方
https://www.acwing.com/problem/content/792/
#include<bits/stdc++.h>
using namespace std;
int main(){
double n; cin>>n;
//确定边界
double l=-1000,r=1000;
while(r-l>1e-8){
double mid=(l+r)/2;
if(mid*mid*mid>=n) r=mid;
else l=mid;
}
printf("%.6lf",l);
return 0;
}
高精度
高精度加法
#include<bits/stdc++.h>
using namespace std;
vector<int> a,b;
vector<int> add(vector<int> &a,vector<int> &b){
vector<int> c;
int t=0;
for(int i=0;i<a.size()||i<b.size();i++){
if(i<a.size()) t+=a[i];
if(i<b.size()) t+=b[i];
c.push_back(t%10);
t/=10;
}
if(t) c.push_back(t);
return c;
}
int main(){
string s1,s2; cin>>s1>>s2;
for(int i=s1.size()-1;i>=0;i--) a.push_back(s1[i]-'0');
for(int i=s2.size()-1;i>=0;i--) b.push_back(s2[i]-'0');
auto c = add(a,b);
for(int i=c.size()-1;i>=0;i--) cout<<c[i];
return 0;
}
高精度减法
#include<bits/stdc++.h>
using namespace std;
vector<int> a,b;
bool cmp(vector<int> &a,vector<int> &b){
if(a.size()!=b.size()) return a.size()>=b.size();
for(int i=a.size()-1;i>=0;i--){
if(a[i]!=b[i]){
return a[i]>=b[i];
}
}
return true;
}
vector<int> sub(vector<int> &a,vector<int> &b){
vector<int> c;
for(int i=0,t=0;i<a.size();i++){
t=a[i]-t;
if(i<b.size()) t-=b[i];
c.push_back((t+10)%10);
if(t<0) t=1;
else t=0;
}
//去除前导零
while(c.size()>1&&c.back()==0) c.pop_back();
return c;
}
int main(){
string s1,s2; cin>>s1>>s2;
for(int i=s1.size()-1;i>=0;i--) a.push_back(s1[i]-'0');
for(int i=s2.size()-1;i>=0;i--) b.push_back(s2[i]-'0');
if(cmp(a,b)){
auto c = sub(a,b);
for(int i=c.size()-1;i>=0;i--) cout<<c[i];
}else{
auto c = sub(b,a);
cout<<"-";
for(int i=c.size()-1;i>=0;i--) cout<<c[i];
}
return 0;
}
高精度乘法
#include<bits/stdc++.h>
using namespace std;
vector<int> mul(vector<int> &a,int b){
vector<int> c;
int t=0;
for(int i=0;i<a.size()||t;i++){
if(i<a.size()) t+=a[i]*b;
c.push_back(t%10);
t/=10;
}
//去除前导 0
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main(){
string s1; cin>>s1;
int b; cin>>b;
vector<int> a;
for(int i=s1.size()-1;i>=0;i--) a.push_back(s1[i]-'0');
auto c = mul(a,b);
for(int i=c.size()-1;i>=0;i--) cout<<c[i];
return 0;
}
高精度除法
#include<bits/stdc++.h>
using namespace std;
vector<int> div(vector<int> &a,int b,int &r){
vector<int> c;
for(int i=a.size()-1;i>=0;i--){//对A从最高位开始处理
r=r*10+a[i];//将上次的余数*10在加上当前位的数字,便是该位需要除的被除数
c.push_back(r/b);//所得即为商在这一位的数字
r%=b;
}
//由于在除法运算中,高位到低位运算,因此C的前导零都在vector的前面而不是尾部
//,vector只有删除最后一个数字pop_back是常数复杂度,而对于删除第一位没有相应的库函数可以使用
// 而且删除第一位,其余位也要前移,
//因此我们将C翻转,这样0就位于数组尾部,可以使用pop函数删除前导0
reverse(c.begin(),c.end());
while(c.size()>1&&c.back()==0) c.pop_back();
return c;
}
int main(){
string s1; cin>>s1;
int b; cin>>b;
vector<int> a;
for(int i=s1.size()-1;i>=0;i--) a.push_back(s1[i]-'0');
int r=0;
auto c = div(a,b,r);
for(int i=c.size()-1;i>=0;i--) cout<<c[i];
cout<<endl<<r;
return 0;
}
前缀和
一维的
#include<bits/stdc++.h>
using namespace std;
int a[1000010];
int main(){
int n,m; scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
int t; scanf("%d",&t);
a[i]=a[i-1]+t;
}
while(m--){
int l,r; scanf("%d%d",&l,&r);
printf("%d",a[r]-a[l-1]);
if(m!=0) printf("\n");
}
return 0;
}
二维的
eg: 子矩阵的和
#include<bits/stdc++.h>
using namespace std;
int n,m,q;
const int maxn = 1010;
int a[maxn][maxn],s[maxn][maxn];
int main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
}
while(q--){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);
}
return 0;
}
差分
一维的
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000010
int a[maxn],b[maxn];
int n,m;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1];
}
//牢记 a数组是 b数组的前缀和
while(m--){
int l,r,c; cin>>l>>r>>c;
b[l]+=c;//
b[r+1]-=c;//这里要记得-c 不然 a 数组后面的会被多 +c
}
for(int i=1;i<=n;i++){
a[i]=a[i-1]+b[i];//这里就是移项了一下
cout<<a[i]<<" ";
}
return 0;
}
双指针
最长不重读子序列
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000010
int n,ans=0;
int a[maxn],b[maxn];
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0,j=0;i<n;i++){
b[a[i]]++;
while(j<i&&b[a[i]]>1) b[a[j++]]--;
ans=max(ans,i-j+1);
}
cout<<ans;
return 0;
}
基础数据结构
单调队列
#include<bits/stdc++.h>
using namespace std;
int n,k,hh=0,tt=-1;// hh 单调队列头部 tt 单调队列尾部
int a[1000010],q[1000010];// q数组用来装 单调队列元素的下标
int main(){
cin.tie(0);
cin>>n>>k;
for(int i=0;i<n;i++){
cin>>a[i];
//检查是否超过窗口长度 若超过则 对头 +1
if(i-q[hh]+1>k) hh++;
//判断队列是否单调递增(求的是窗口最小值,队头则是最小值)
while(hh<=tt&&a[q[tt]]>=a[i]) tt--;
q[++tt]=i;
if(i+1>=k) cout<<a[q[hh]]<<" ";
}
cout<<endl;
hh=0,tt=-1;
for(int i=0;i<n;i++){
if(i-q[hh]+1>k) hh++;
while(hh<=tt&&a[q[tt]]<=a[i]) tt--;
q[++tt]=i;
if(i+1>=k) cout<<a[q[hh]]<<" ";
}
return 0;
}
单调栈
#include<bits/stdc++.h>
using namespace std;
int tot,sta[1000010];
int main(){
cin.tie(0);
int n; cin>>n;
while(n--){
int x; cin>>x;
while(tot&&sta[tot]>=x) tot--;
if(!tot) cout<<"-1 ";
else cout<<sta[tot]<<" ";
sta[++tot] = x;
}
return 0;
}
单链表
#include<bits/stdc++.h>
using namespace std;
#define maxn 100010
int head,nex[maxn],val[maxn],idx;
void init(){
head = -1;
idx=0;
}
//插入到头结点
void insertHead(int x){
val[idx] = x;
nex[idx]=head;
head = idx++;
}
//将x插到下标是k的点后面
void insertOne(int k,int x){
val[idx] = x;
nex[idx] = nex[k];
nex[k] = idx++;
}
// 将下标是k的点后面的点删掉
void remove(int k){
nex[k] = nex[nex[k]];
}
int main(){
init();
int m; cin>>m;
while(m--){
string s; cin>>s;
if(s=="H"){
int x; cin>>x;
insertHead(x);
}else{
if(s=="D"){
int k; cin>>k;
if (!k) head = nex[head];
remove(k-1);
}else{
int k,x; cin>>k>>x;
insertOne(k-1,x);
}
}
}
for(int i=head;i != -1 ;i = nex[i]){
cout<<val[i]<<" ";
}
return 0;
}
Trie树
快速存储字符集合和快速查询字符集合
//Trie树快速存储字符集合和快速查询字符集合
#include <iostream>
using namespace std;
const int N = 100010;
//son[][]存储子节点的位置,分支最多26条;
//cnt[]存储以某节点结尾的字符串个数(同时也起标记作用)
//idx表示当前要插入的节点是第几个,每创建一个节点值+1
int son[N][26], cnt[N], idx;
char str[N];
void insert(char *str)
{
int p = 0; //类似指针,指向当前节点
for(int i = 0; str[i]; i++)
{
int u = str[i] - 'a'; //将字母转化为数字
if(!son[p][u]) son[p][u] = ++idx; //该节点不存在,创建节点
p = son[p][u]; //使“p指针”指向下一个节点
}
cnt[p]++; //结束时的标记,也是记录以此节点结束的字符串个数
}
int query(char *str)
{
int p = 0;
for(int i = 0; str[i]; i++)
{
int u = str[i] - 'a';
if(!son[p][u]) return 0; //该节点不存在,即该字符串不存在
p = son[p][u];
}
return cnt[p]; //返回字符串出现的次数
}
int main()
{
int m;
cin >> m;
while(m--)
{
char op[2];
scanf("%s%s", &op, &str);
if(*op == 'I') insert(str);
else printf("%d\n", query(str));
}
return 0;
}
作者:四谷夕雨
链接:https://www.acwing.com/solution/content/14695/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
并查集

合并集合
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int p[N];
int find(int x) {
if (x == p[x]) //如果x是祖先,则返回
return x;
else
return find(p[x]); //如果x不是祖先,则x的爸爸 问 x的爷爷
}
//路径压缩的find函数
int find2(int x) {
if (x != p[x]) // x不是自身的父亲,即x不是该集合的代表
p[x] = find(p[x]); // 查找x的祖先直到找到代表,于是顺手路径压缩
return p[x];
}
int main() {
int n, m;
cin >> n >> m;
// 记录某个人的爸爸是谁,特别规定,祖先的爸爸是他自己
for (int i = 1; i <= n; i++) p[i] = i;
while (m--) {
string op;
cin >> op;
int a, b;
cin >> a >> b;
if (op == "M") p[find(a)] = find(b);
else if (op == "Q") {
if (find(a) == find(b)) puts("Yes");
else puts("No");
}
}
}
作者:松鼠爱葡萄
链接:https://www.acwing.com/solution/content/19232/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
连通块中点的数量
#include<bits/stdc++.h>
using namespace std;
int n,m;
int p[1000010];
int sz[1000010];
int findx(int x){
if(x!=p[x]) p[x]=findx(p[x]);
return p[x];
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
p[i]=i;
sz[i]=1;
}
while(m--){
string s; cin>>s;
if(s=="C"){
int a,b; cin>>a>>b;
if(findx(a)==findx(b)) continue;
sz[findx(b)]+=sz[findx(a)];
p[findx(a)]=findx(b);
}else
if(s=="Q1"){
int a,b; cin>>a>>b;
if(findx(a)==findx(b)) cout<<"Yes\n";
else cout<<"No\n";
}else{
int a; cin>>a;
cout<<sz[findx(a)]<<"\n";
}
}
return 0;
}
堆

堆排序
//如何手写一个堆?完全二叉树 5个操作
//1. 插入一个数 heap[ ++ size] = x; up(size);
//2. 求集合中的最小值 heap[1]
//3. 删除最小值 heap[1] = heap[size]; size -- ;down(1);
//4. 删除任意一个元素 heap[k] = heap[size]; size -- ;up(k); down(k);
//5. 修改任意一个元素 heap[k] = x; up(k); down(k);
#include <iostream>
using namespace std;
int const N = 100010;
//h[i] 表示第i个结点存储的值,i从1开始,2*i是左子节点,2*i + 1是右子节点
//size 既表示堆里存储的元素个数,又表示最后一个结点的下标
int h[N], siz; //堆有两个变量h[N],size; 怎么这里的size和文件里有冲突,只能改成siz了
void down(int u)
{
int t = u;//t存储三个结点中存在的最小的结点的下标,初始化为当前结点u
if (u * 2 <= siz && h[u * 2] < h[t]) t = u * 2; // 左子节点存在并且小于当前结点,更新t的下标
if (u * 2 + 1 <= siz && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//右子节点存在并且小于当前结点,更新t的下标
if (t != u)//如果t==u意味着不用变动,u就是三个结点中拥有最小值的结点下标,否则交换数值
{
swap(h[t], h[u]);
down(t); //交换数值后,t这个结点存储原本u的值,u存储存储t的值(三个数中的最小值)。u不用调整了,但t情况不明,可能需要调整。直到它比左右子节点都小
}
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
siz = n; //初始化size,表示堆里有n 个元素
for (int i = n / 2; i; i --) down(i); //把堆初始化成小根堆,从二叉树的倒数第二行开始,把数字大的下沉
while (m -- )
{
printf("%d ", h[1]);
h[1] = h[siz];
siz --;
down(1);
}
return 0;
}
作者:现代修士o_O
链接:https://www.acwing.com/solution/content/46535/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
模拟堆
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
const int N = 1e5 + 10;
int h[N]; /* 堆 */
int ph[N]; /* 存储第k个插入的数在堆中的下标 */
int hp[N]; /* 存储堆中指定下标的值是第k个插入的数,与ph[N]互逆 */
int cnt; /* 存储当前堆中用到了哪个下标,用于插入与删除等操作 */
void heap_swap(int a, int b)
{
swap(ph[hp[a]], ph[hp[b]]); /* 1.先通过下标a找到h[a]在堆中是第几个插入的数
2.再通过第几个插入的数k找到在ph中所记录的在
堆中对应的下标 3.最后与b交换 */
swap(hp[a], hp[b]); /* 交换所记录的在堆中插入的值的顺序 */
swap(h[a], h[b]); /* 交换堆中的值 */
}
void down(int u)
{
int t = u;
if (u * 2 <= cnt && h[u * 2] < h[t])
t = u * 2;
if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t])
t = u * 2 + 1;
if (u != t) /* 如果u不是当前以u为根节点的堆的最小值 */
{
heap_swap(u , t);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u] < h[u / 2]) {
heap_swap(u, u / 2);
u >>= 1;
}
}
int main()
{
int n, m = 0;
cin >> n;
while (n--) {
char op[5];
int k, x;
cin >> op;
if (!strcmp(op, "I")) {
cin >> x;
cnt ++;
m ++;
ph[m] = cnt; /* 堆中第m个插入的数在堆中的下标是cnt */
hp[cnt] = m; /* 堆中下标为cnt的数是在堆中是第m个插入的 */
h[cnt] = x;
up(cnt);
}
else if (!strcmp(op, "PM"))
cout << h[1] << endl;
else if (!strcmp(op, "DM")) {
heap_swap(1, cnt);
cnt --;
down(1);
}
else if (!strcmp(op, "D")) {
cin >> k;
k = ph[k]; /* 取得第k个插入的数在堆中的下标 */
heap_swap(k, cnt);
cnt --;
up(k);
down(k);
}
else if (!strcmp(op, "C")) {
cin >> k >> x;
k = ph[k];
h[k] = x;
up(k);
down(k);
}
}
return 0;
}
作者:17835208153
链接:https://www.acwing.com/solution/content/29198/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
搜索
DFS
全排列
#include<bits/stdc++.h>
using namespace std;
int n;
int a[10];
bool b[10];
int dfs(int x){
if(x==n){
for(int i=0;i<n;i++) cout<<a[i]<<" ";
cout<<"\n";
return 0;
}
for(int i=1;i<=n;i++){
if(!b[i]){
a[x]=i;
b[i]=true;
dfs(x+1);
b[i]=false;
}
}
}
int main(){
cin>>n;
dfs(0);
return 0;
}
n皇后
#include<bits/stdc++.h>
using namespace std;
const int N=10;
char ans[N][N];
int n;
int col[N],dg[N],udg[N];
void dfs(int u){
if(n==u){
for(int i=0;i<n;i++) puts(ans[i]);
return ;
}
for(int i=0;i<n;i++){
if(!col[i]&&!dg[n+i]&&!udg[n-i+u]){
ans[u][i]='Q';
col[i]=dg[n+i]=udg[n-i+u]=true;
dfs(u+1);
ans[u][i]='.';
col[i]=dg[n+i]=udg[n-i+u]=false;
}
}
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ans[i][j]='.';
dfs(0);
return 0;
}
n皇后原始版
#include<bits/stdc++.h>
using namespace std;
char ans[10][10];
int n;
int row[10],col[10],dg[10],udg[10];
void dfs(int x,int y,int s){
if(y==n) y=0,x++;
if(x==n){
if(s==n){
for(int i=0;i<n;i++) puts(ans[i]);
puts("");
}
return ;
}
//不放皇后
dfs(x,y+1,s);
//放皇后
if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[x-y+n]){
ans[x][y]='Q';
row[x]=col[y]=dg[x+y]=udg[x-y+n]=true;
dfs(x,y+1,s+1);
row[x]=col[y]=dg[x+y]=udg[x-y+n]=false;
ans[x][y]='.';
}
}
int main(){
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ans[i][j]='.';
dfs(0,0,0);
return 0;
}
树的重心
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图,所以每个节点至多对应2n-2条边
int h[N]; //邻接表存储树,有n个节点,所以需要n个队列头节点
int e[M]; //存储元素
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入,n个节点
int ans = N; //表示重心的所有的子树中,最大的子树的结点数目
bool st[N]; //记录节点是否被访问过,访问过则标记为true
//a所对应的单链表中插入b a作为根
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// dfs 框架
/*
void dfs(int u){
st[u]=true; // 标记一下,记录为已经被搜索过了,下面进行搜索过程
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]) {
dfs(j);
}
}
}
*/
//返回以u为根的子树中节点的个数,包括u节点
int dfs(int u) {
int res = 0; //存储 删掉某个节点之后,最大的连通子图节点数
st[u] = true; //标记访问过u节点
int sum = 1; //存储 以u为根的树 的节点数, 包括u,如图中的4号节点
//访问u的每个子节点
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
//因为每个节点的编号都是不一样的,所以 用编号为下标 来标记是否被访问过
if (!st[j]) {
int s = dfs(j); // u节点的单棵子树节点数 如图中的size值
res = max(res, s); // 记录最大联通子图的节点数
sum += s; //以j为根的树 的节点数
}
}
//n-sum 如图中的n-size值,不包括根节点4;
res = max(res, n - sum); // 选择u节点为重心,最大的 连通子图节点数
ans = min(res, ans); //遍历过的假设重心中,最小的最大联通子图的 节点数
return sum;
}
int main() {
memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
cin >> n; //表示树的结点数
// 题目接下来会输入,n-1行数据,
// 树中是不存在环的,对于有n个节点的树,必定是n-1条边
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a); //无向图
}
dfs(1); //可以任意选定一个节点开始 u<=n
cout << ans << endl;
return 0;
}
作者:松鼠爱葡萄
链接:https://www.acwing.com/solution/content/13513/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
BFS
迷宫
#include<bits/stdc++.h>
using namespace std;
int n,m;
typedef pair<int,int> PII; //用来存点,用pair方便点点
const int N=110; //数据范围
int g[N][N],d[N][N];// g数组装整个图, d数组表示某点到原点的距离
int bfs(){
queue<PII> q;
q.push({0,0});//首先起点入队
memset(d,-1,sizeof d);//将最开始的所有点到起点的距离都设置为-1
d[0][0]=0;//起点到起点的距离设置为0,
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0}; /*方向数组,随便向那个方向扩展都得行,
我的是上(x不变,y会加1)右(x会加1,y不变)下(x不变,y会减1)左(x会减1,y不变)*/
while(!q.empty()){
auto t = q.front();//取出队首元素
q.pop();//队首出队
for(int i=0;i<4;i++){//向4个方向扩展
// x,y 为扩展后的, t装的是拓展前的坐标
int x=t.first+dx[i];
int y=t.second+dy[i];
//满足边界条件,拓展的点的位置没有障碍,在之前没有被访问过(距离为-1就表示没访问过)
if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&d[x][y]==-1){
d[x][y]=d[t.first][t.second]+1;//更新距离
q.push({x,y});//将成功扩展的点入队
}
}
}
return d[n-1][m-1];//最终 d[n-1][m-1] 就是右下角到左上角的需要移动的最短距离
}
int main(){
cin>>n>>m;
//读入图的信息
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
cin>>g[i][j];
cout<<bfs()<<"\n";//输出结果
}
有向图的拓扑序列
#include<bits/stdc++.h>
using namespace std;
int n, m;
const int N = 1000010;
int h[N], ne[N], e[N], idx;
int d[N];//d数组表示某点的入度
void add(int a,int b){//存储图,以邻接表的方式
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int q[N];//定义个队列(数组模拟队列),装入度为0的点。 (这也可以不用队列,就看做是个普通的数组也行)
int topSe(){
int hh = 0, tt = 0;//初始化队头和队尾
for (int i = 1; i <= n;i++){
if(!d[i]) q[tt++] = i; //把入度为0的点入队
}
while(hh<=tt){//队列不空就执行下面的
int t = q[hh++];//取出队头的数,然后将对头的数出队。(这就是数组模拟队列的优点吧)
for (int i = h[t]; i != -1;i=ne[i]){//遍历头结点的出边
int j = e[i];//获取到达的点
d[j]--;//将出边能到达的点,把入度减1(就是把边删掉)
if(d[j]==0){//如果结点的入度为0
d[j] = d[t] + 1;//距离 在上一个点的距离基础上 +1
q[tt++] = j;//将这个入度为0的点加入队列
}
}
}
return tt == n;//队列长度等于n,返回1,否则返回0
}
int main(){
memset(h, -1, sizeof(h));//将h数组全部置为-1,(这个看自己的写法,和上面得第20行有关)
cin >> n >> m;
for (int i = 0; i < m;i++){
int a, b;
cin >> a >> b;
add(a, b);
d[b]++;//因为是 a -> b ,所以,b 的入度要加 1
}
if(topSe()){//如果存在拓扑序列,则输出
for (int i = 0; i <n;i++)//我们可以发现,队列中的入队顺序就是拓扑序列
cout << q[i] << " ";
cout << "\n";
}else //不存在则输出-1
cout << "-1\n";
return 0;
}
图论
最短路
dijkstra朴素版
#include<bits/stdc++.h>
using namespace std;
#define maxn 510
//g数组存的是邻接矩阵,d数组存的是某点到起点的最短距离,
//st数组是用来装确定了的点(确定了到起点的距离最短的点)
int g[maxn][maxn],d[maxn],st[maxn];
int n,m;
int dijkstra(){
memset(d,0x3f,sizeof(d));//先将所有距离设为最大
d[1]=0;//起点到起点的距离为0
for(int i=0;i<n;i++){//找出每个点到起点的距离,每次寻找不在st中距离最近的点t
int t=-1;//用于更新第一个点,这个比较巧妙
for(int j=1;j<=n;j++){//寻找不在st中,距离最近的点t
if(!st[j]&&(t==-1||d[j]<d[t])) t=j;
}
st[t]=true;//将t加入到st中,表示已经确定了这个点
for(int j=1;j<=n;j++){//通过t点来更新其它点的距离
d[j]=min(d[j],d[t]+g[t][j]);
}
}
d[n]!=0x3f3f3f3f?cout<<d[n]:cout<<-1;//输出答案
return 0;
}
int main(){
cin>>n>>m;
memset(g,0x3f,sizeof(g));//因为是求的最小值,所以初始化为无穷大
while(m--){
int a,b,c;
cin>>a>>b>>c;
g[a][b]=min(g[a][b],c); //在重边中去取得最小值
}
dijkstra();//调用
return 0;
}
dijkstra堆优化版
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010; // 把N改为150010就能ac
// 稀疏图用邻接表来存
int h[N], e[N], ne[N], idx;
int w[N]; // 用来存权重
int dist[N];
bool st[N]; // 如果为true说明这个点的最短路径已经确定
int n, m;
void add(int x, int y, int c)
{
w[idx] = c; // 有重边也不要紧,假设1->2有权重为2和3的边,再遍历到点1的时候2号点的距离会更新两次放入堆中
e[idx] = y; // 这样堆中会有很多冗余的点,但是在弹出的时候还是会弹出最小值2+x(x为之前确定的最短路径),并
ne[idx] = h[x]; // 标记st为true,所以下一次弹出3+x会continue不会向下执行。
h[x] = idx++;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap; // 定义一个小根堆
// 这里heap中为什么要存pair呢,首先小根堆是根据距离来排的,所以有一个变量要是距离,其次在从堆中拿出来的时
// 候要知道知道这个点是哪个点,不然怎么更新邻接点呢?所以第二个变量要存点。
heap.push({ 0, 1 }); // 这个顺序不能倒,pair排序时是先根据first,再根据second,这里显然要根据距离排序
while(heap.size())
{
PII k = heap.top(); // 取不在集合S中距离最短的点
heap.pop();
int ver = k.second, distance = k.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i]; // i只是个下标,e中在存的是i这个下标对应的点。
if(dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({ dist[j], j });
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(h, -1, sizeof(h));
scanf("%d%d", &n, &m);
while (m--)
{
int x, y, c;
scanf("%d%d%d", &x, &y, &c);
add(x, y, c);
}
cout << dijkstra() << endl;
return 0;
}
作者:optimjie
链接:https://www.acwing.com/solution/content/6554/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
bellman-ford
有边数限制的最短路
#include<bits/stdc++.h>
using namespace std;
const int N = 510, M = 10010;
struct Edge{
int a, b, w;
} e[M];//把每个边保存下来
int dist[N], backup[N];//backup数组是备份数组,防止串联
int n, m, k;
int bellman_ford(){
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
for (int i = 0; i < k;i++){
memcpy(backup, dist, sizeof(dist));
for (int j = 0; j < m;j++){//遍历所有边
int a = e[j].a, b = e[j].b, w = e[j].w;
dist[b] = min(dist[b], backup[a] + w);
}
}
return dist[n] >= 0x3f3f3f3f / 2 ? -2 : dist[n];
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> m >> k;
for (int i = 0; i < m;i++){
int a, b, w;
cin >> a >> b >> w;
e[i] = {a, b, w};
}
int ans = bellman_ford();
if(ans!=-2) cout << ans;
else cout << "impossible";
return 0;
}
SPFA
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int h[N],ne[N],e[N],w[N],idx;
int dist[N],st[N];
int n,m;
void add(int a,int b,int c){
w[idx]=c;
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
int spfa(){
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
queue<int> q;
q.push(1);
st[1]=true;
while(q.size()){
int t = q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
if(!st[j]){
q.push(j);
st[j]=true;
}
}
}
}
return dist[n]==0x3f3f3f3f?-2:dist[n];
}
int main(){
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--){
int a,b,w;
cin>>a>>b>>w;
add(a,b,w);
}
int ans=spfa();
if(ans!=-2) cout<<ans;
else cout<<"impossible";
return 0;
}
SPFA判断是否存在负环
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int dist[N],st[N],ct[N];
int h[N],e[N],ne[N],w[N],idx;
int n,m;
void add(int a,int b,int c){
w[idx]=c;
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
int spfa(){
queue<int> q;
for(int i=1;i<=n;i++){
q.push(i);
st[i]=true;
}
while(q.size()){
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
ct[j]=ct[t]+1;
if(ct[j]>n) return true;
if(!st[j]){
q.push(j);
st[j]=true;
}
}
}
}
return false;
}
int main(){
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--){
int a,b,c; cin>>a>>b>>c;
add(a,b,c);
}
if(spfa())cout<<"Yes";
else cout<<"No";
return 0;
}
Floyd算法
#include<bits/stdc++.h>
using namespace std;
const int N=210;
int d[N][N];
int n,m,k;
int INF=1e9;
void floyed(){
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i==j) d[i][j]=0;
else d[i][j]=INF;
while(m--){
int x,y,z; cin>>x>>y>>z;
d[x][y]=min(d[x][y],z);
}
floyed();
while(k--){
int x,y; cin>>x>>y;
int ans=d[x][y];
if(ans>=INF/2) cout<<"impossible\n";
else cout<<ans<<"\n";
}
return 0;
}
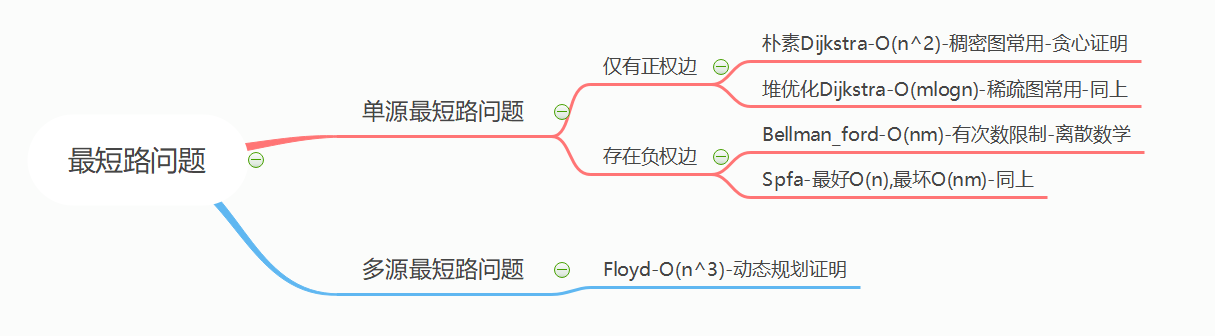
最短路总结(acwing上的)

最小生成树
prim求最小生成树
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int INF = 0x3f3f3f3f;
int dist[N],g[N][N];
bool st[N];
int n,m;
int prim(){
int res=0;
memset(dist,INF,sizeof(dist));
for(int i=0;i<n;i++){
int t=-1;
for(int j=1;j<=n;j++){
if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;
}
if(i&&dist[t]==INF) return INF;
st[t]=true;
if(i)res+=dist[t];
for(int j=1;j<=n;j++){
dist[j]=min(dist[j],g[t][j]);
}
}
return res;
}
int main(){
cin>>n>>m;
memset(g,0x3f,sizeof(g));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i ==j) g[i][j] = 0;
else g[i][j] = INF;
while(m--){
int a,b,c; cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c);
}
int res = prim();
if(res==INF) cout<<"impossible\n";
else cout<<res<<"\n";
return 0;
}
Kruskal算法求最小生成树
#include<bits/stdc++.h>
using namespace std;
const int N=100010,M=200010,INF = 0x3f3f3f3f;
int n,m;
int p[N];
struct Edg{
int a,b,w;
// bool operator< (const Edg &W)const{
// return w<W.w;
// }
}e[M];
bool cmp(Edg a,Edg b){
return a.w<b.w;
}
int find(int x){
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int kruskal(){
sort(e,e+m,cmp);
for(int i=1;i<=n;i++) p[i]=i;
int res=0,cnt=0;
for(int i=0;i<m;i++){
int a=e[i].a,b=e[i].b,w=e[i].w;
a=find(a),b=find(b);
if(a!=b){
p[a]=b;
res+=w;
cnt++;
}
}
return cnt<n-1?INF:res;
}
int main(){
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,w;
cin>>a>>b>>w;
e[i]={a,b,w};
}
int ans=kruskal();
if(ans==INF) cout<<"impossible\n";
else cout<<ans<<"\n";
return 0;s
}
二分图
染色法判定二分图
#include<bits/stdc++.h>
using namespace std;
const int N=100010,M=200010;
int h[N],e[M],ne[M],idx;
int st[M];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int u,int color){
st[u]=color;
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]){
if(!dfs(j,3-color)) return false;
}else if(st[j]==color) return false;
}
return true;
}
int main(){
int n,m;
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--){
int a,b;
cin>>a>>b;
add(a,b);add(b,a);
}
bool flag=true;
for(int i=1;i<=n;i++){
if(!st[i]){
if(!dfs(i,1)){
flag=false;
break;
}
}
}
if(flag) cout<<"Yes\n";
else cout<<"No\n";
return 0;
}
匈牙利算法
二分图的最大匹配
#include<bits/stdc++.h>
using namespace std;
const int N = 510, M = 100010;
int h[N],e[M],ne[M],idx;
int n1,n2,m;
int match[N];
bool st[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int find(int x){
for(int i=h[x];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]){
st[j]=true;
if(match[j]==0||find(match[j])){
match[j]=x;
return true;
}
}
}
return false;
}
int main(){
memset(h,-1,sizeof(h));
cin>>n1>>n2>>m;
while(m--){
int a,b; cin>>a>>b;
add(a,b);
}
int res=0;
for(int i=1;i<=n1;i++){
memset(st,false,sizeof(st));
if(find(i)) res++;
}
cout<<res;
return 0;
}
本文来自博客园,作者:后端小知识,转载请注明原文链接:https://www.cnblogs.com/tiancx/p/15391337.html

