二维空间内的三角剖分2 -- (给出边缘顶点的例子)
之前的三角剖分, 居然弄的如此复杂, 再也不相信百度了......
换一种思路, 首先给出的顶点是连续的顶点, 那么可以以一种农村包围城市的方法来划分, 我们只需要沿着顺序不断获取Pa, Pb, Pc三点, 然后检测他们是否构成三角形(不在一条直线上)并且没有其它顶点在三角形内, 然后通过剔除顶点的方式继续划分, 就能把三角形一个个分解出来, 虽然都是简单划分, 对于复杂的比如自相交它还是不能正确计算, 可是相比之前的简直又快又简单, 看下面图解:
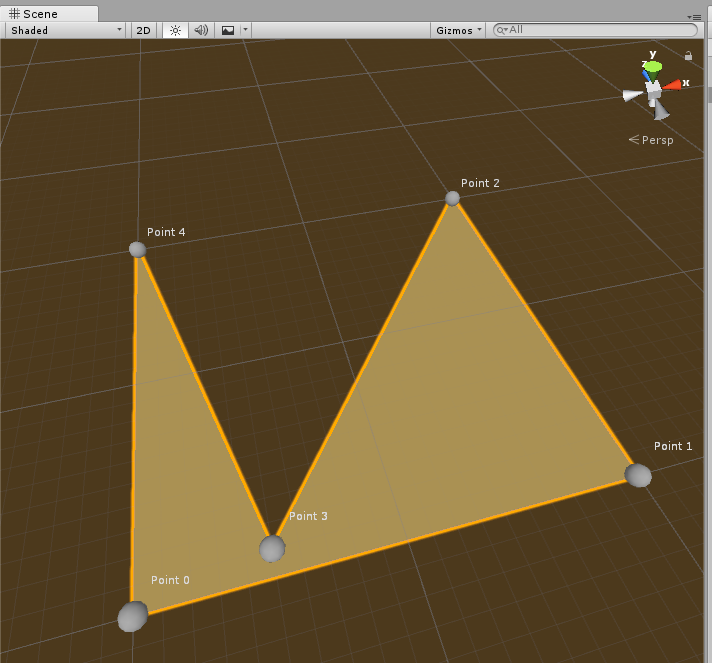
沿着给出的边无限循环取点, 比如先取[0, 1, 2] 然后测试到 Point 3 在它们构成的三角形内, 就跳过继续取点[1, 2, 3] 然后检测没有点在其中, 这就得到第一个三角形了:
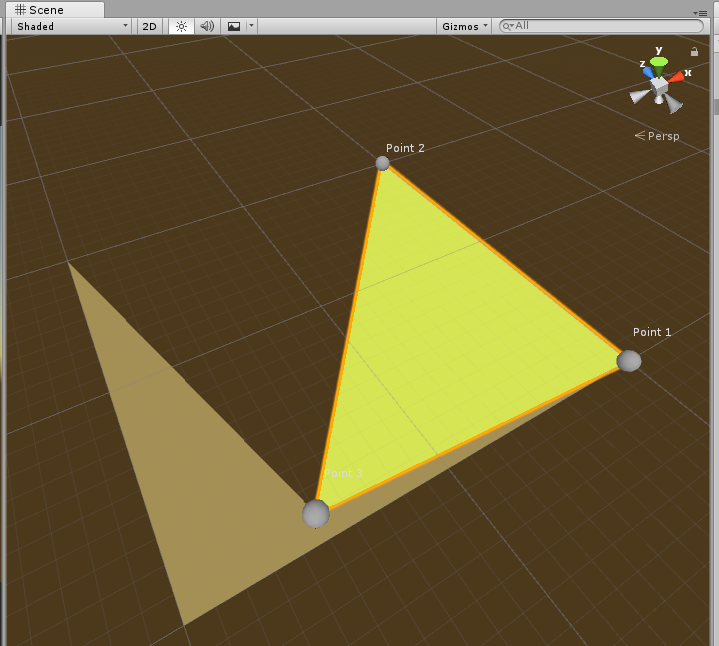
然后将位于中间的点剔除出顶点列表, 这样等于得到最外围的某个三角形了, 好像农村包围城市一样, 剔除掉 Point 2 之后继续进行测试, 获取 [3, 4, 5] 构成的三角形, 一次类推...

顶点反向也可以正常计算出来.
代码:
public class Triangulator { private List<Vector2> m_points = new List<Vector2>(); public Triangulator(List<Vector2> points) { m_points = points; } public int[] Triangulate() { List<int> indices = new List<int>(); int n = m_points.Count; if(n < 3) { return indices.ToArray(); } int[] V = new int[n]; if(Area() > 0) { for(int v = 0; v < n; v++) { V[v] = v; } } else { for(int v = 0; v < n; v++) { V[v] = (n - 1) - v; } } int nv = n; int count = 2 * nv; for(int v = nv - 1; nv > 2;) { if((count--) <= 0) { return indices.ToArray(); } int u = v; if(nv <= u) { u = 0; } v = u + 1; if(nv <= v) { v = 0; } int w = v + 1; if(nv <= w) { w = 0; } if(Snip(u, v, w, nv, V)) { int a, b, c, s, t; a = V[u]; b = V[v]; c = V[w]; indices.Add(a); indices.Add(b); indices.Add(c); for(s = v, t = v + 1; t < nv; s++, t++) { V[s] = V[t]; } nv--; count = 2 * nv; } } indices.Reverse(); return indices.ToArray(); } private float Area() { int n = m_points.Count; float A = 0.0f; for(int p = n - 1, q = 0; q < n; p = q++) { Vector2 pval = m_points[p]; Vector2 qval = m_points[q]; A += pval.x * qval.y - qval.x * pval.y; //Cross } return (A * 0.5f); // Triangle Size } // can this triangle be clipped? private bool Snip(int u, int v, int w, int n, int[] V) { int p; Vector2 A = m_points[V[u]]; Vector2 B = m_points[V[v]]; Vector2 C = m_points[V[w]]; if(Mathf.Epsilon > (((B.x - A.x) * (C.y - A.y)) - ((B.y - A.y) * (C.x - A.x)))) { return false; // 三边重合以及方向检测 } for(p = 0; p < n; p++) { if((p == u) || (p == v) || (p == w)) { continue; } Vector2 P = m_points[V[p]]; if(InsideTriangle(A, B, C, P)) { return false; } } return true; } // P inside triangle[A,B,C] public static bool InsideTriangle(Vector2 A, Vector2 B, Vector2 C, Vector2 P) { var pa = (A - P); var pb = (B - P); var pc = (C - P); var crossA = CrossVec2(pa, pb); var crossB = CrossVec2(pb, pc); var crossC = CrossVec2(pc, pa); bool inside = (crossA >= 0 && crossB >= 0 && crossC >= 0) || (crossA <= 0 && crossB <= 0 && crossC <= 0); return inside; } public static float CrossVec2(Vector2 a, Vector2 b) { return (a.x * b.y) - (a.y * b.x); } }
它最重要的逻辑是 Area() 这个函数, 它通过叉乘计算了一个面积, 而影响了原始点的排列顺序, 然后影响到 Snip 逻辑, 之后再研究...






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律