深入浅出之切空间
这是我以前在其它地方写的, 转到这里来, 这里的排版比较好看.
添加了新的内容, 比如法线贴图和切空间的概念等(2019.07.04)
----------- 下面首先这是别人写的切空间的原理, 因为难懂所以我才写了一个新的版本的在后面 -----------
法线贴图中的法线向量在切线空间中，法线永远指着正z方向。切线空间是位于三角形表面之上的空间：法线相对于单个三角形的本地参考框架。它就像法线贴图向量的本地空间；
它们都被定义为指向正z方向，无论最终变换到什么方向。使用一个特定的矩阵我们就能将本地/切线空寂中的法线向量转成世界或视图坐标，使它们转向到最终的贴图表面的方向。 我们可以说，上个部分那个朝向正y的法线贴图错误的贴到了表面上。法线贴图被定义在切线空间中，所以一种解决问题的方式是计算出一种矩阵，把法线从切线空间变换到一个不同的空间，
这样它们就能和表面法线方向对齐了：法线向量都会指向正y方向。切线空间的一大好处是我们可以为任何类型的表面计算出一个这样的矩阵，由此我们可以把切线空间的z方向和表面的法线方向对齐。 这种矩阵叫做TBN矩阵这三个字母分别代表tangent、bitangent和normal向量。这是建构这个矩阵所需的向量。要建构这样一个把切线空间转变为不同空间的变异矩阵，
我们需要三个相互垂直的向量，它们沿一个表面的法线贴图对齐于：上、右、前；已知上向量是表面的法线向量。右和前向量是切线(Tagent)和副切线(Bitangent)向量。
下面的图片展示了一个表面的三个向量
计算出切线和副切线并不像法线向量那么容易。从图中可以看到法线贴图的切线和副切线与纹理坐标的两个方向对齐。我们就是用到这个特性计算每个表面的切线和副切线的。需要用到一些数学才能得到它们；请看下图：
上图中我们可以看到边纹理坐标的不同，是一个三角形的边，这个三角形的另外两条边是和，它们与切线向量和副切线向量方向相同。这样我们可以把边和用切线向量和副切线向量的线性组合表示出来（注意和都是单位长度，在平面中所有点的T，B坐标都在0到1之间，
因此可以进行这样的组合）：
我们也可以写成这样：
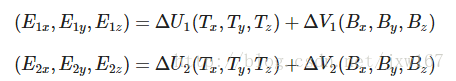
是两个向量位置的差，和是纹理坐标的差。然后我们得到两个未知数（切线T和副切线B）和两个等式。你可能想起你的代数课了，这是让我们去接和。
上面的方程允许我们把它们写成另一种格式：矩阵乘法
尝试会意一下矩阵乘法，它们确实是同一种等式。把等式写成矩阵形式的好处是，解和会因此变得很容易。两边都乘以的逆矩阵等于：
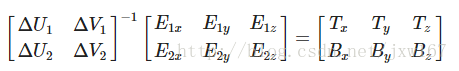
这样我们就可以解出和了。这需要我们计算出delta纹理坐标矩阵的拟阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的共轭矩阵。
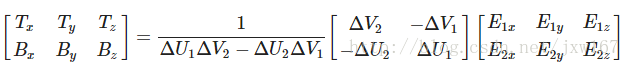
有了最后这个等式，我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量和副切线。
我们可以用TBN矩阵把所有向量从切线空间转到世界空间，传给像素着色器，然后把采样得到的法线用TBN矩阵从切线空间变换到世界空间；法线就处于和其他光照变量一样的空间中了。
我们用TBN的逆矩阵把所有世界空间的向量转换到切线空间，使用这个矩阵将除法线以外的所有相关光照变量转换到切线空间中；这样法线也能和其他光照变量处于同一空间之中。
我们来看看第一种情况。我们从法线贴图重采样得来的法线向量，是以切线空间表达的，尽管其他光照向量是以世界空间表达的。把TBN传给像素着色器，我们就能将采样得来的切线空间的法线乘以这个TBN矩阵，
将法线向量变换到和其他光照向量一样的参考空间中。这种方式随后所有光照计算都可以简单的理解。
以上就是别人写的攻略, 我表示有看没有懂, 就自己写一个吧
-------------------------- 我是分割线 --------------------------
好吧看完我要跪了, 有图有文, 可是看不懂, 我就来个深入浅出版本吧:
先说明什么是法线贴图 :
法线贴图就是提供给模型表面作为其法线的一张贴图, 或者叫凹凸贴图, 一般用来提高模型细节, 比如说一个墙壁模型师做成一个简单Quad, 然后加上凹凸贴图就能在光照的时候表现出墙面的凹凸效果了.
然后什么是切空间 :
法线贴图提取出来的向量, 它不是一个本地向量, 是基于该点所在的模型的三角面上的, 也就是基于切空间的, 那么问题来了, 这个法线它的方向是朝向哪里的? 也就是说这个法线的切空间坐标系是哪里来的呢? 我们看下图 :
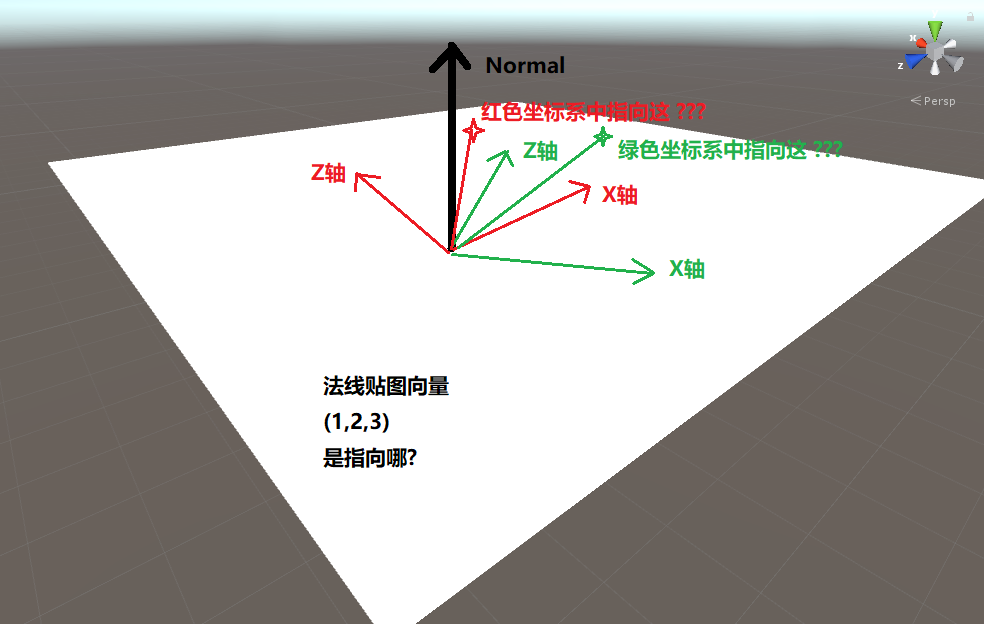
图中可见, 如果要组成一个在这个面上的坐标系, 有无数种, 这些都是切空间坐标系.
我们按照美术制作的流程 (假) 来解释比较容易明白, 首先美术做了一个面, 在这个面上要添加凹凸法线, 然后如果他选择了红色坐标系, 那么这个点的法线的向量可能是(1,2,3), 如果他选择了绿色的坐标系, 这个法线的向量可能就是(2,3,4)了,
他选择的坐标系就叫切空间了. 那么我们要怎样方便快捷地知道切空间呢? 是要美术在模型的每一个面上都附加一个坐标系信息吗? 还真是, 请看下图:
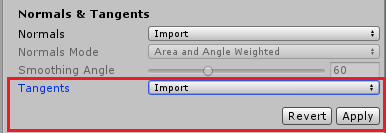
一个模型, 它的切空间信息是可以导入的, 也就是说模型是可以附带切空间信息的. 那么一个切空间信息应该是怎样的呢? 很简单, 因为模型的每个面都是有向量的 (当做Y轴), 那么我们再有一个其它的轴 (X轴或Z轴), 然后叉积就能计算出另外一个轴了.
所以导入模型的选项中可以选择导入Tangents, 这里的X轴一般被称为Tangent轴. Z轴被叫做Bitangent轴. Y轴就是Normal了.
到这里你可能就慌了, 知道了切空间的各个轴, 也知道了在切空间中的凹凸法线向量, 那么怎样把凹凸法线变换到世界坐标系中啊??? 很简单, 先把凹凸法线转换到本地坐标系, 然后转换到世界坐标系.
比如:
凹凸法线向量 (r, g, b) 一般使用r对应X轴, g对应Z轴, b对应Y轴, 所以法线贴图一般偏蓝, 就是偏向法线方向.
切空间各个坐标轴向量(切空间相对于本地坐标系) :
X轴 : (x0, y0, z0) -> Tangent
Y轴 : (x1, y1, z1) -> Normal
Z轴 : (x2, y2, z2) -> Bitangent
那么转换到本地坐标系就是 localNormal = normalize(Tangent * r + Normal * b + Bitangent * g), 数学理论不用说了, 初中生的知识. 再转到世界坐标系就用 Transform.localToWorldMatrix 计算即可, 非常简单. 看到这里就不虚了吧.
我们继续往下看, 原来切空间还能通过计算得出来?
为什么呢? 如果美术同学在导出模型的时候没有导出切空间信息给我们, 还能通过计算得到? 计算得到的跟美术同学制作时使用的切空间能一样吗?
答案是 : 可以计算得到, 计算出来的切空间跟美术制作时使用的是一样的. 是不是又开始慌了? 不是说一个面上的切空间有无数种吗? 为什么能逆计算出来呢? 答案就在UV坐标中.
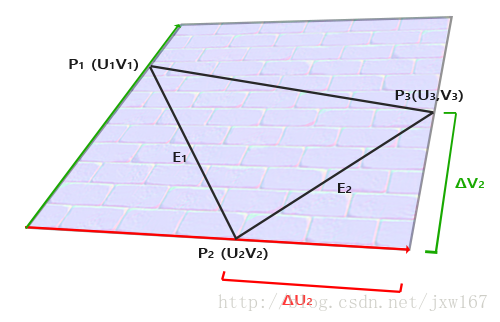
前面的文章是假设了T, B两个三维向量, 使用差值来计算的, 假设有三个点 :
P1 (x1, y1, z1) 对应UV(u1, v1)
P2 (x2, y2, z2) 对应UV(u2, v2)
P3 (x3, y3, z3) 对应UV(u3, v3)
那么假设T,B向量为正交向量在三角平面上:
P2-P1 = T * (u2-u1) + B * (v2-v1)
P3-P1 = T * (u3-u1) + B * (v3-v1)
根据上面文章的计算, 这个T,B向量是唯一的, 根据现代工程原理, 那么一般来说美术制作所使用的软件, 它也是根据模型的顶点位置和UV来给出切空间的, 然后美术同学就在给出的切空间去做凹凸贴图, 而不是由他来自定义切空间.
所以切空间是可以根据逆计算得到的.
下面是从几何原理来说明切空间:
先从shader怎样使用凹凸贴图开始说, 原理很简单, 首先你想要给一个模型提供法线贴图, 那么在每一个Fragment阶段都要去取NormalMap的rgb当做法线来用, 流程如下:
1. 用uv取出NormalMap相应的rgb作为tangentNormal, 它的rgb的b值是我们通常的法线方向. 见图一
2. 把这个tangentNormal贴到uv相应的插值点的Local坐标位置(图二), 因为它表现的是这个点的切空间中的法线方向, 必然要转换到本地坐标系, 转换之后它就是这个点的LocalNormal了.
如图一是tangentNormal的rgb(xyz)方向. 图二表示这个图元在模型的一个面上, tangentNormal在转换后的方向也发生了改变.
3. 把LocalNormal转到世界就是该插值点的世界法线了WorldNormal. 完毕.
图一
图二
通过代码梳理流程, 以下是某老外写的, 思路非常清晰 :
1. GetTangentSpaceNormal就是把法线贴图的向量弄出来
2. 获取出来的tangentSpaceNormal就是切空间中的向量, 注意这里使用了rgb的b来作为Y轴方向, 这是约定俗成的.
3. i.tangent (X轴), binormal (Z轴), i.normal (Y轴) 代表的就是当前三角面的切空间相对于LocalSpace的坐标系, 这样跟tangentSpaceNormal的每个值相乘, 就相当于把向量投影到本地坐标系了.
// 把法线贴图的向量弄出来
float3 GetTangentSpaceNormal (Interpolators i) { float3 normal = float3(0, 0, 1); #if defined(_NORMAL_MAP) normal = UnpackScaleNormal(tex2D(_NormalMap, i.uv.xy), _BumpScale); #endif #if defined(_DETAIL_NORMAL_MAP) float3 detailNormal = UnpackScaleNormal(tex2D(_DetailNormalMap, i.uv.zw), _DetailBumpScale); detailNormal = lerp(float3(0, 0, 1), detailNormal, GetDetailMask(i)); normal = BlendNormals(normal, detailNormal); #endif return normal; }
void InitializeFragmentNormal(inout Interpolators i) { float3 tangentSpaceNormal = GetTangentSpaceNormal(i); #if defined(BINORMAL_PER_FRAGMENT) float3 binormal = CreateBinormal(i.normal, i.tangent.xyz, i.tangent.w); #else float3 binormal = i.binormal; #endif i.normal = normalize(tangentSpaceNormal.x * i.tangent + tangentSpaceNormal.z * i.normal + tangentSpaceNormal.y * binormal); }
这里可能有点没有说清楚, i.tangent, binormal, i.normal其实都是三角形面上基于LocalSpace坐标系的新坐标系(切空间), 而它的法线就是i.normal.
因为NormalMap的b(z)表示的是垂直方向, 所以用tangentSpaceNormal.z * i.normal 来获得在新坐标系中法线方向的值.
FragmentOutput MyFragmentProgram (Interpolators i) { float alpha = GetAlpha(i); #if defined(_RENDERING_CUTOUT) clip(alpha - _AlphaCutoff); #endif InitializeFragmentNormal(i);
......
}
看, 在Fragment中修改法线方向
在前面的流程梳理中很自然地忽略了一个过程: 怎样获得Tangent和Bitangent轴.实际上就是获得一个在三角形面上的坐标系, 我们将LocalSpace坐标系作为原始坐标系, 而在模型三角形面上的坐标系(切空间)就是LocalSpace坐标系的子坐标系,
它的每个轴的描述是用LocalSpace坐标系作为参照的.所以Tangent的计算可以直接在模型阶段就预先计算好, 作为本地数据存储即可.
那么Tangent和Bitangent轴到底是怎样计算出来的呢, 以现有数据来看, 我们只知道三角形面的几个顶点坐标, 以及该面的Normal(法线), 那么在这个三角形上构建的坐标系可以是无穷多的, 只要符合在面上的两个正交向量+法线即可,
看下图 :
法线(红)+蓝色 或 法线(红)+绿色 都能构建一个坐标系. 法线贴图获取的向量在不同坐标系里面的方向肯定是不同的. 要怎样才能构建唯一正确的切空间坐标系呢...回到法线贴图来,
当把这个贴图贴在某个模型上时, 比如在下图中, 喷涂区域贴在了某个三角面上 :
喷涂区域就是对应的三角面, 那么就简单了, 如果我们把这张2D图片做成一个3D中的平面的话, 我们通过拉伸, 平移旋转等各种方法把对应的三角形区域跟模型上的重叠起来的话, 那么该3D平面的两个边就成了Tangent和Bitangent轴了,
理解了的话就可以 回去看开篇的数学公式了 往下看了. 下图我把中国地图贴在了一个三角形上(假设是在模型的本地坐标系中), 然后还做了一个3D平面挂上贴图.
我通过各种方法使他们图片重叠了, 这样我的3D图片的两个边 ( 当然方向是UV的正方向 ) 就成为了切空间的Tangent和Bitangent了 (当然计算切空间不可能这样神手动).
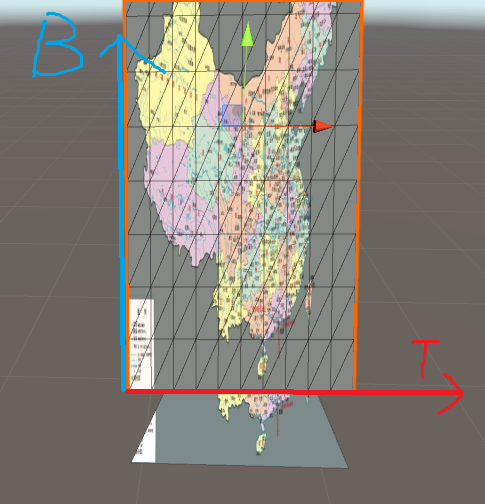
希望这个能够讲清楚切空间的逻辑流程.
PS: 模型每个顶点都带有position, uv, 所以计算Tangent这些数据并不依赖于图片, 不要被上面我的手动误导了哈
下来详细讲解数学流程吧...还是用中国地图来说:
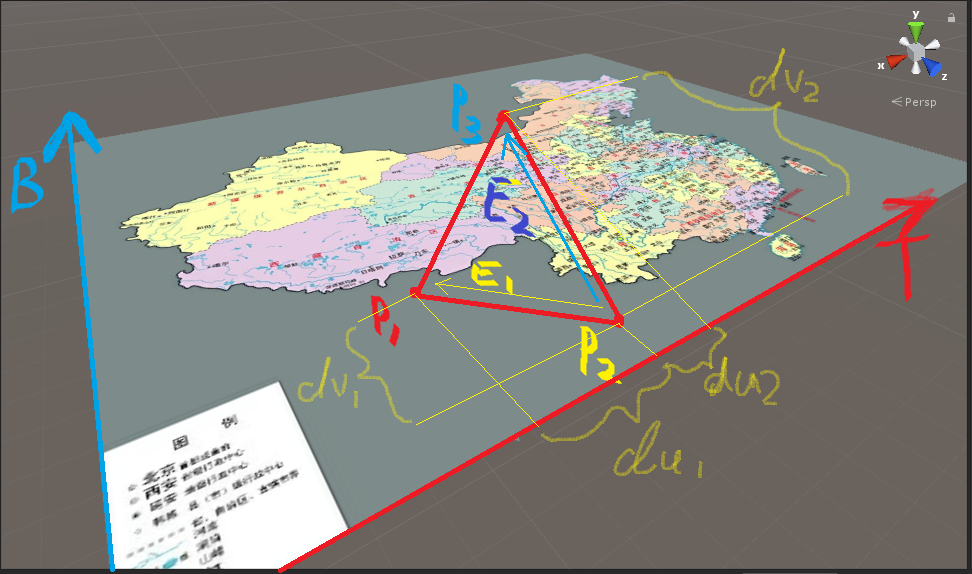
P1,P2,P3 就是模型三角形面的三个点了, 他们带有位置和UV信息.
P1{X1, Y1, Z1, U1, V1}
P2{X2, Y2, Z2, U2, V2}
P3{X3, Y3, Z3, U3, V3}
E1{P1 - P2} (X, Y, Z)
E2{P3 - P2} (X, Y, Z)
注意, 这是计算用到的中间变量, 与取哪个点的先后无关, 与哪个点的相对位置也无关, 不管怎样取只要能表现出三角形的任意两条边即可.
du1, du2, dv1, dv2 分别表示E1, E2代表的向量在uv上的差值
注意, 这里因为要求得的向量只有T,B所以需要两个行列式即可, 所以上面的数据只取了三角形的任意两条边, 以及他们的增量数据du/dv.
变量就这些, 它已经提供了我们所需的数据了
1. 它有了实际空间中的两个向量E1, E2
2. 它提供了向量增长的方向的参考数据du1, dv1, du2, dv2, 也就是说E1,E2在T,B坐标系下是如何增长的(因为UV就是沿着T,B增长的), 反过来也就可以求出T,B的向量了.
PS -- 这里可以把T,B坐标系看成是有边界的坐标系(UV值就是坐标系中的位置所占的百分比), 之后的计算能够进行全依赖于UV坐标是个归一化数据, 在任何缩放下都不受影响的功劳.
之后就可以开始写等式了:
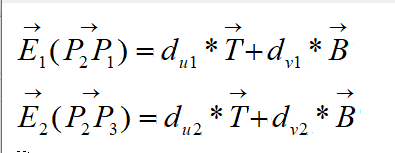
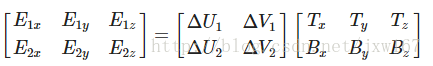
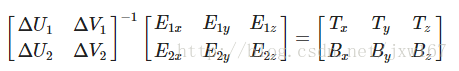
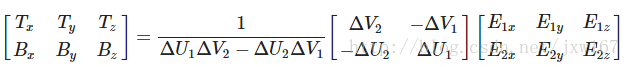
var p1 = new Vector3(1, 3, 5); var p2 = new Vector3(2, 3, 8); var p3 = new Vector3(0, 1, 4); var uv1 = new Vector2(0, 0); var uv2 = new Vector2(0.5f, 0.5f); var uv3 = new Vector2(1, 0); var E1 = p1 - p2; var E2 = p3 - p2; var duv1 = uv1 - uv2; var duv2 = uv3 - uv2; float multi = 1.0f / (duv1.x * duv2.y - duv2.x * duv1.y); var matrixUV = new Matrix4x4(); matrixUV[0, 0] = duv2.y; matrixUV[0, 1] = -duv1.y; matrixUV[1, 0] = -duv2.x; matrixUV[1, 1] = duv1.x; var matrixE = new Matrix4x4(); matrixE.SetRow(0, new Vector4(E1.x, E1.y, E1.z, 0)); matrixE.SetRow(1, new Vector4(E2.x, E2.y, E2.z, 0)); var finalMatrix = (matrixUV * matrixE); var tangent = new Vector3(finalMatrix[0, 0], finalMatrix[0, 1], finalMatrix[0, 2]) * multi; var bitangent = new Vector3(finalMatrix[1, 0], finalMatrix[1, 1], finalMatrix[1, 2]) * multi; var normal = Vector3.Cross(E2, E1); Debug.Log("计算的Normal 归一化 : " + normal.normalized); Debug.Log("计算的Tangent 归一化 : " + tangent.normalized); Debug.Log("计算的Bitangent 归一化 : " + bitangent.normalized); Debug.Log("Tangent 与 Bitangent 垂直? " + Vector3.Dot(tangent, bitangent)); var go = GameObject.CreatePrimitive(PrimitiveType.Quad); var mesh = new Mesh(); mesh.vertices = new Vector3[] { p1, p2, p3 }; mesh.triangles = new int[] { 0, 1, 2 }; mesh.uv = new Vector2[] { uv1, uv2, uv3 }; mesh.RecalculateNormals(); mesh.RecalculateTangents(); go.GetComponent<MeshFilter>().mesh = mesh; var meshTangents = mesh.tangents; var meshNormals = mesh.normals; for(int i = 0, imax = Mathf.Min(meshTangents.Length, meshNormals.Length); i < imax; i++) { var n = new Vector3(meshNormals[i].x, meshNormals[i].y, meshNormals[i].z); Debug.Log("Mesh的Normal 归一化 : " + n.normalized); var t = new Vector3(meshTangents[i].x, meshTangents[i].y, meshTangents[i].z); Debug.Log("Mesh的Tangent 归一化 : " + meshTangents[i]); Debug.Log("Mesh的Bitangent 归一化 : " + Vector3.Cross(t, n).normalized); } }
结果 :
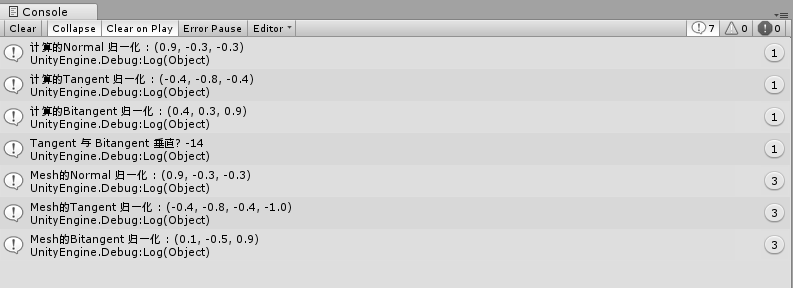
直接给出三个点和对应的UV值, 通过理论计算出Tangent, Bitangent, Normal等值, 打印出来, 然后生成Mesh, 用Mesh自带的计算功能计算相关值,
也打印出来, 可以看到Normal和Tangent在前后两种模式下得到的都是一样的, 而Bitangent在两种计算中完全不一样, 并且在理论计算中甚至Bitangent和Tangent不是正交的,
这是为什么呢? 看前面的等式:
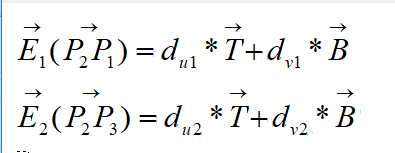
这个等式显然没有设定T向量一定跟B向量正交, 这是数学上的解释, 从几何上来说的话, 按照上面我写的几何论证过程, 就是说原图像要覆盖到三角形上需要经过拉伸旋转等操作,
使得Tangent / Bitangent坐标轴也被拉伸旋转了, 导致T, B不再是正交的了. 看图理解 :
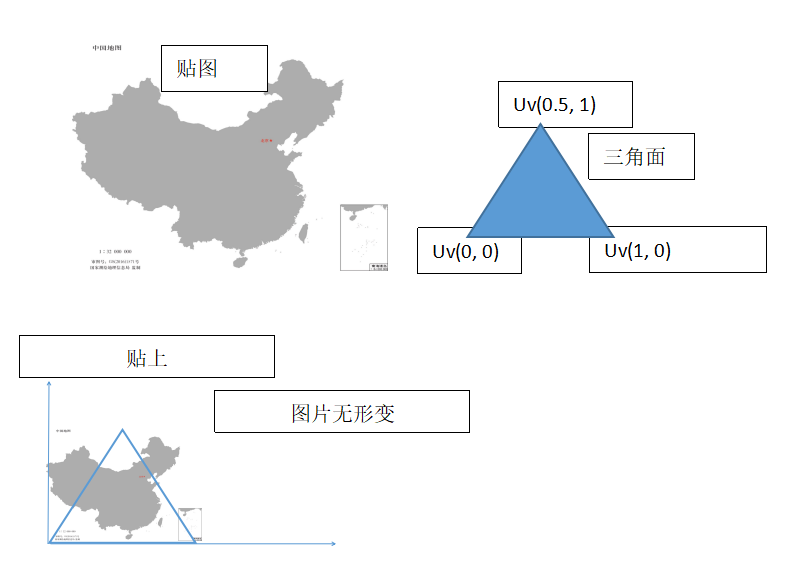
注 : 右图的中国地图应该是拉伸的平行四边形, 用WORD做的没办法表现出来
所以可以看出, 在理论计算中的Bitangent方向跟Tangent方向有可能正交也可能不正交. 取决于UV对图片的拉伸. 不过我们需要的只有Tangent, 不管在美术制作还是
自动计算, 切空间都是先计算出Tangent然后叉积算出Bitangent, 而理论计算出来的Bitangent并不是切空间的Z轴, 请注意.
写了这么多应该很清楚了吧. 在我写之前有几个问题一直没搞清楚, 这里自问自答了.
提问 : Tangent轴是不是就是三角形的某一个边? 如果是的话就不用这么复杂计算半天了吧?
有可能是, 也有可能不是, 参考数学逻辑, 只有在特殊情况下才有E1 == T 或E2 == T. 或者几何方法看看上面的图片, 如果上面的三角形的Uv(1,0)这个点变成Uv(1, 0.5)的话, Tangent轴也是跟三角形的边是错开的.
提问 : 理论计算的Bitangent轴它的意义是什么? 没用的话可以省点计算量吗?
它跟Tangent一样是对等的, 如果我们取Bitangent作为基础轴的话, Tangent就是没用的了, 反之就是我们现在约定俗成地使用Tangent轴, 其实最省事的是直接使用三角形的某条边做Tangent才是最省计算量的, 可是
三角形有三条边, 不是唯一, 不同的平台有不同的表达. 而Tangent计算出来是唯一的.
