既然有一致性哈希，就肯定还有不一致哈希，为啥平时没人说不一致哈希呢？因为常见的哈希都是不一致的，所以就不修饰了，到了一致性哈希才特殊加个描述词修饰一下。

哈希一般都是将一个大数字取模然后分散到不同的桶里，假设我们只有两个桶，有 2、3、4、5 四个数字，那么模 2 分桶的结果就是：


这时我们嫌桶太少要给哈希表扩容加了一个新桶，这时候所有的数字就需要模 3 来确定分在哪个桶里，结果就变成了：


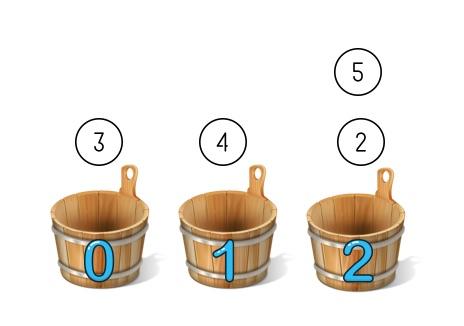
可以看到新加了一个桶后所有数字的分布都变了，这就意味着哈希表的每次扩展和收缩都会导致所有条目分布的重新计算，这个特性在某些场景下是不可接受的。比如分布式的存储系统，每个桶就相当于一个机器，文件分布在哪台机器由哈希算法来决定，这个系统想要加一台机器时就需要停下来等所有文件重新分布一次才能对外提供服务，而当一台机器掉线的时候尽管只掉了一部分数据，但所有数据访问路由都会出问题。这样整个服务就无法平滑的扩缩容，成为了有状态的服务。

要想实现无状态化，就要用到一致性哈希了，一致性哈希中假想我们有很多个桶，先定一个小目标比如 7 个，但一开始真实还是只有两个桶，编号是 3 和 6。哈希算法还是同样的取模，只不过现在分桶分到的很可能是不存在的桶，那么就往下找找到第一个真实存在的桶放进去。这样 2 和 3 都被分到了编号为 3 的桶， 4 和 5 被分到了编号为 6 的桶。


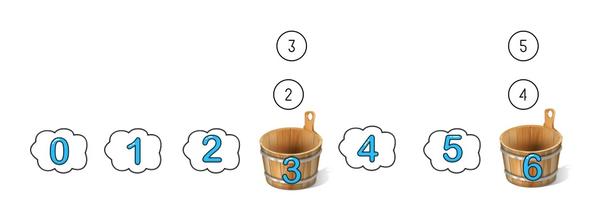
这时候再添加一个新的桶，编号是 4，取模方法不变还是模 7：


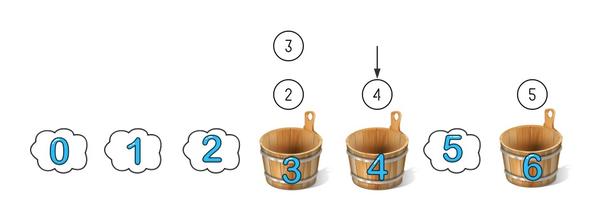
因为 3 号桶里都是取模小于等于 3 的，4 号桶只需要从 6 号桶里拿走属于它的数字就可以了，这种情况下只需要调整一个桶的数字就可分成了重新分布。可以想象下即使有 1 亿个桶，增加减少一个桶也只会影响一个桶的数据分布。

这样增加一个机器只需要和他后面的机器同步一下数据就可以开始工作了，下线一个机器需要先把他的数据同步到后面一台机器再下线。如果突然掉了一台机器也只会影响这台机器上的数据。实现中可以让每台机器同步一份自己前面机器的数据，这样即使掉线也不会影响这一部分的数据服务。

这里还有个小问题要是编号为 6 的机桶下线了，它没有后一个桶了，数据该咋办？为了解决这个问题，实现上通常把哈希空间做成环状，这样 3 就成了 6 的下一桶，数据给 3 就好了：


用一致性哈希还能实现部分的分布式系统无锁化，每个任务有自己的编号，由于哈希算法的确定性，分到哪个桶也是确定的就不存在争抢，也就不需要分布式锁了。

既然一致性哈希有这么多好的特性，那为啥主流的哈希都是非一致的呢？主要一个原因在于查找效率上，普通的哈希查询一次哈希计算就可以找到对应的桶了，算法时间复杂度是 O(1)，而一致性哈希需要将排好序的桶组成一个链表，然后一路找下去，k 个桶查询时间复杂度是 O(k)，所以通常情况下的哈希还是用不一致的实现。

当然 O(k) 的时间复杂度对于哈希来说还是不能忍的，想一下都是O(k) 这个量级了用哈希的意义在哪里？既然是在排好序的桶里查询，很自然的想法就是二分了，能把时间复杂度降到 O(logk)，然而桶的组合需要不断的增减，所以是个链表的实现，二分肯定就不行了，还好可以用跳转表进行一个快速的跳转也能实现 O(logk) 的时间复杂度。


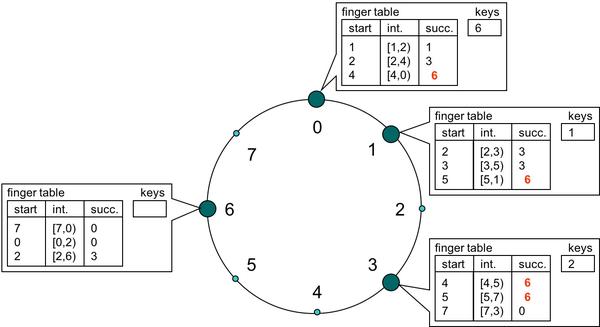
在这个跳转表中，每个桶记录距离自己 1，2，4 距离的数字所存的桶，这样不管查询落在哪个节点上，对整个哈希环上任意的查询一次都可以至少跳过一半的查询空间，这样递归下去很快就可以定位到数据是存在哪个桶上。

当然这写都只是一致性哈希实现方式中的一种，还有很多实现上的变体。比如选择数字放在哪个桶，上面的介绍里是选择顺着数字下去出现的第一个桶，其实也可以选择距离这个数字最近的桶，这样实现和后面的跳转表规则也会有变化。同样跳转表也有多种不同的算法实现，感兴趣的可以去看一下 CAN，Chord，Tapestry，Pastry 这四种 DHT 的实现，有意思的是它们都是 2001 年发出来的 paper，所以 2001 年大概是 P2P 下载的元年吧。