BatchNorm归一化

BatchNorm

BatchNorm

BatchNorm原理

论文：https://arxiv.org/pdf/1502.03167v3.pdf

深层神经网络在做非线性变换前的激活输入值，随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，

一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近，导致训练收敛慢。

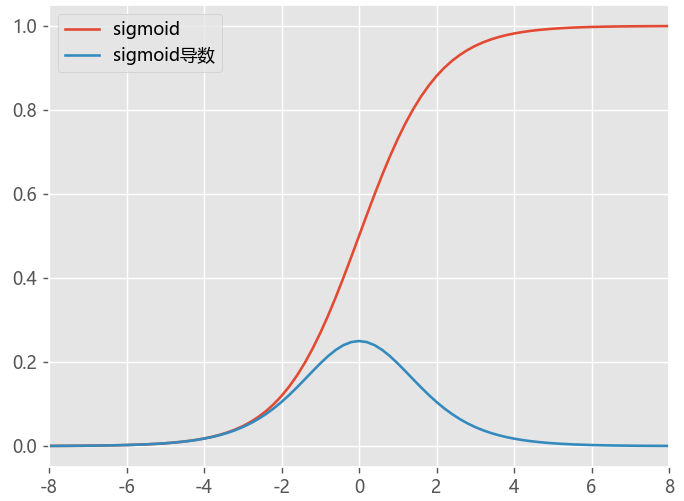
对于Sigmoid函数来说，，每一次参数迭代更新后，上一层网络的输出数据经过这一层网络计算后，数据的分布会发生变化,
更加倾向于向 激活函数的两端进行分布，导致反向传播时低层神经网络的梯度消失，训练收敛变慢
对数据做归一化当然可以加快训练速度，能对数据做去相关性，突出它们之间的分布相对差异就更好了

BN的目的及思想
BN的公式
BN的优点
BN的BP推导
BN的代码实现

目的及思想

为了解决深层网络难以训练的问题。深度神经网络之所以难以训练是因为每一层输入的分布在训练期间会随着前一层参数变化而变化，就要求我们必须使用一个很小的学习率和对参数很好的初始化，但是这样么做会让训练过程变得很慢。“每一层输入的分布在训练期间会随着前一层参数变化而变化

BN的思想是对每层隐藏层的输入做一个正态标准化处理（使激活函数的输入（Z）的均值为0，方差为1）。其实这个和预处理中的对特征做归一化基本一样

我们对特征做归一化也是为了代价函数能够更快的收敛，加快训练速度，这和BN的思想都是一致的。

BN的公式步骤

1 、首先求出此次批量样本 x的均值

2、求出此次批量的样本方差

3、对 x 进行归一化操作得到 x （标准化处理）

4、引入缩放和平移变量计算最后的归一化数值（平移和缩放）

在BN中，一共有四个参数

$ \gamma , \beta $：分别是仿射中的 weights 和 bias 待学习，用于控制y的方差和均值

$ \mu, \sigma _{}^{2} $ 和上面的参数不同，这两个是根据输入的batch的统计特性计算的

平移和缩放作用

保证模型的表达能力不因为标准化而下降

如果直接只做标准化不做其他处理，神经网络是学不到任何东西的，因为标准化之后都是标准分布了，但是加入这两个参数后就不一样了。

BN的反向传播

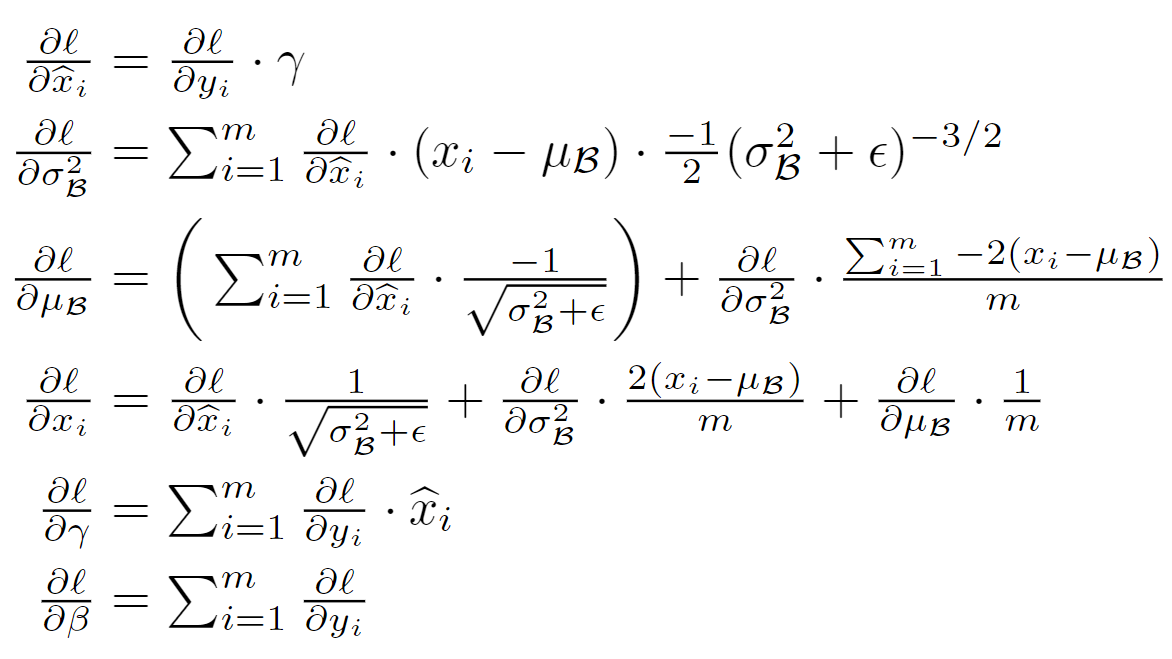
详细参考：

https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html

https://blog.csdn.net/weixin_42211626/article/details/122855967

BN优缺点

经过标准化，每层神经网络的输出变成了均值为0，方差为1的标准分布,数据分布不再受其他神经元影响

0、BN层让损失函数更平滑，使得后面的网络层更具有鲁棒性，BN更有利于梯度下降。

1、可以使用更大的学习率，训练过程更加稳定，极大提高了训练速度。

2、Batch Normalization具有某种正则作用，不需要太依赖dropout，减少过拟合。

3、对权重初始化不再敏感，通常权重采样自0均值某方差的高斯分布

4、BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题

缺点：

Batch Size太小，则BN效果明显下降

RNN等动态网络使用BN效果不佳

图像分割这类任务, batch size 只能是个位数, 表现不佳

对于像素级图像生成任务表现不佳

训练测试的区别

BN一般要求将训练集完全打乱

训练阶段：首先计算均值和方差（每次训练给一个批量，计算批量的均值方差），然后归一化，然后缩放和平移。

对每一批数据进行归一化到一个相同的分布，而每一批数据的均值和方差会有一定的差别，而不是用固定的值，这个差别实际上也能够增加模型的鲁棒性，并会在一定程度上减少过拟合。

测试阶段：使用计算好全局的 mean、 var ，直接使用，不再计算

代码实现

def batchnorm_forward(x, gamma, beta, eps):

  N, D = x.shape
  #为了后向传播求导方便，这里都是分步进行的
  #step1: 计算均值
  mu = 1./N * np.sum(x, axis = 0)

  #step2: 减均值
  xmu = x - mu

  #step3: 计算方差
  sq = xmu ** 2
  var = 1./N * np.sum(sq, axis = 0)

  #step4: 计算x^的分母项
  sqrtvar = np.sqrt(var + eps)
  ivar = 1./sqrtvar

  #step5: normalization->x^
  xhat = xmu * ivar

  #step6: scale and shift
  gammax = gamma * xhat
  out = gammax + beta

  #存储中间变量
  cache =  (xhat,gamma,xmu,ivar,sqrtvar,var,eps)

  return out, cache


def batchnorm_backward(dout, cache):

  #unfold the variables stored in cache
  xhat,gamma,xmu,ivar,sqrtvar,var,eps = cache

  #get the dimensions of the input/output
  N,D = dout.shape

  #step9
  dbeta = np.sum(dout, axis=0)
  dgammax = dout #not necessary, but more understandable

  #step8
  dgamma = np.sum(dgammax*xhat, axis=0)
  dxhat = dgammax * gamma

  #step7
  divar = np.sum(dxhat*xmu, axis=0)
  dxmu1 = dxhat * ivar

  #step6
  dsqrtvar = -1. /(sqrtvar**2) * divar

  #step5
  dvar = 0.5 * 1. /np.sqrt(var+eps) * dsqrtvar

  #step4
  dsq = 1. /N * np.ones((N,D)) * dvar

  #step3
  dxmu2 = 2 * xmu * dsq

  #step2
  dx1 = (dxmu1 + dxmu2)
  dmu = -1 * np.sum(dxmu1+dxmu2, axis=0)

  #step1
  dx2 = 1. /N * np.ones((N,D)) * dmu

  #step0
  dx = dx1 + dx2

  return dx, dgamma, dbeta

import torch
import torch.nn as nn
net = nn.BatchNorm1d(1, momentum=0, eps=0, affine=False)
x = torch.tensor([-1, 1], dtype=torch.float, requires_grad=True)
y = nn.ReLU()(net(x.view(-1, 1))).sum()
y.backward()
print(x.grad) # tensor([0., 0.])