torch常见激活函数
torch常见激活函数
目录
激活函数定义
激活函数（也称“非线性映射函数”） 不使用激活函数的话，神经网络的每层都只是做线性变换，多层输入叠加后也还是线性变换。因为线性模型的表达能力通常不够，所以这时候就体现了激活函数的作用了，激活函数可以引入非线性因素
激活函数的性质
1. 连续并可导(允许少数点上不可导)的非线性函数。可导的激活函数 可以直接利用数值优化的方法来学习网络参数。
2. 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
3. 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性.
Sigmoid型S激活函数
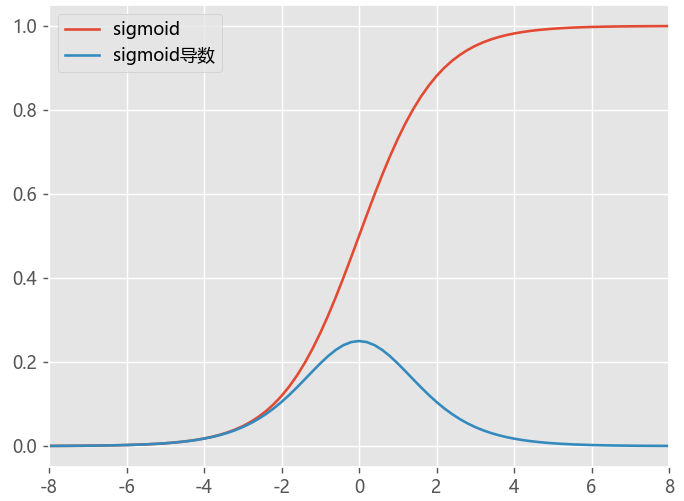
sigmoid函数
\[f(x)=\frac{1}{1+e^{-x} } ~~~~~~~~~ 导数 \acute{f} (x)-\frac{e^{-x}}{(1+e^{-x})^2} =f(x)(1-f(x))
\]
它的特点是将输入值映射到0到1之间的连续范围内，输出值具有良好的可解释性，但是它在梯度消失和输出饱和等问题上表现不佳。
- Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到 1，因此它对每个神经元的输出进行了归一化；控制输出约束
- 概率的取值范围是 0 到 1，用于将预测概率作为输出的模型
- 梯度平滑 无跳跃
- 缺点，容易出现梯度消失gradient vanishing，具有幂运算，计算复杂度较高
- Sigmoid函数的输出值恒大于0 导致模型训练速度收敛变慢
def sigmoid(x):
"""1.0 / (1.0 + exp(-x))"""
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_du(x):
return sigmoid(x) * (1.0 - sigmoid(x))
def plotloss(act_func,act_name):
plt.style.use('ggplot')
plt.rcParams["font.sans-serif"]=["Microsoft YaHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #正常显示负号
fig = plt.figure()
ax = fig.add_subplot(111)
# 1, define input data
inputs = [x for x in np.arange(-8, 9, 0.2)]
# 2, calculate outputs
plt.xlim(-8, 8)
for act,name in zip(act_func,act_name):
outputs = [act(x) for x in inputs]
plt.plot(inputs, outputs, label=name)
plt.legend()
plt.show()
plotloss([sigmoid,sigmoid_du],act_name=['sigmoid','sigmoid导数'])
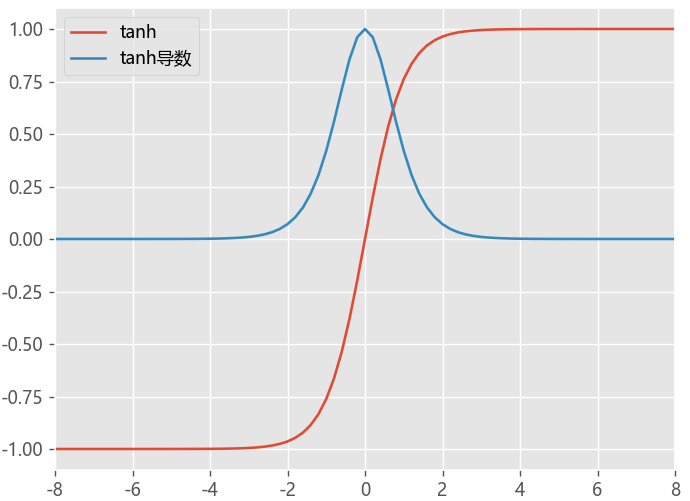
Tanh函数
\[f(x)=\frac{e^{-x}-e^{-x}}{e^{-x}+e^{-x} } =\frac{2}{1+e^{-2x}}-1 ~~~~~~~导数\acute{f} (x)=\frac{4}{(e^x+e^{-x})^2}=1-{f(x)}^2
\]
Tanh函数是一种具有S形状的激活函数，其特点是将输入值映射到-1到1之间的连续范围内，输出值也具有良好的可解释性
- 解决了Sigmoid 不是 zero-centered 问题，但是梯度消失的问题任然存在
def tanh(x):
return np.tanh(x)
def tanh_du(x):
return 1.0 - tanh(x)**2
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
def tanh(x):
return np.tanh(x)
def plotloss(act_func,act_name):
plt.style.use('ggplot')
plt.rcParams["font.sans-serif"]=["Microsoft YaHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #正常显示负号
fig = plt.figure()
ax = fig.add_subplot(111)
# 1, define input data
inputs = [x for x in np.arange(-8, 9, 0.2)]
# 2, calculate outputs
plt.xlim(-8, 8)
for act,name in zip(act_func,act_name):
outputs = [act(x) for x in inputs]
plt.plot(inputs, outputs, label=name)
plt.legend()
plt.show()
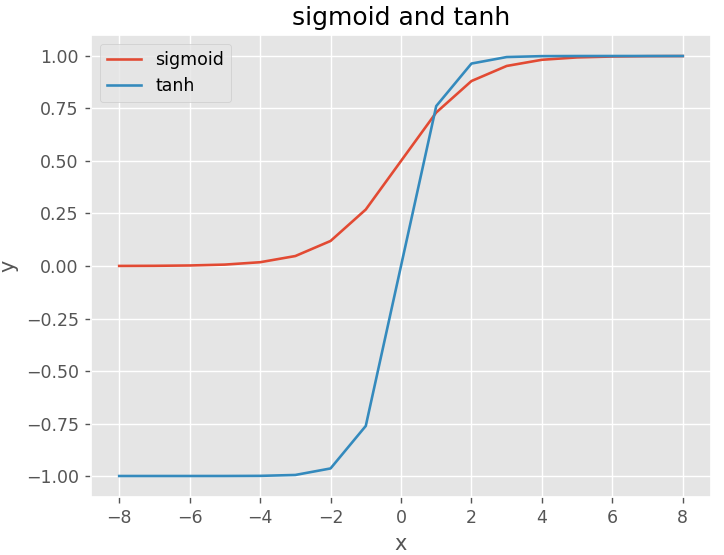
plotloss([sigmoid,tanh],act_name=['sigmoid','tanh'])
LogSigmoid函数
\[f(x)=log( \frac{1}{1+e^{-x} })
\]
LogSigmoid激活函数常常被用作与NULLoss损失函数一起使用，用作神经网络反向传播过程中的计算交叉熵的环节。
def logsigmoid(x):
return np.log(1.0 / (1.0 + np.exp(-x)))
Softmax函数
Softmax函数是一种常用于多分类问题的激活函数，它将输入值映射到0到1之间的概率分布，可以将神经网络的输出转换为各个类别的概率值。Softmax函数的优点是简单、易于理解，并且在多分类问题中表现出色，但是它也存在梯度消失和输出饱和等问题。
def Softmax(x):
exp_x = np.exp(x)
return exp_x / np.sum(exp_x, axis=0, keepdims=True)
Softmax函数：
Softmax激活函数的特点：
1、在零点不可微，
2、负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。
2、将预测结果转化为非负数、预测结果概率之和等于1。
3、经过使用指数形式的Softmax函数能够将差距大的数值距离拉的更大。
在深度学习中通常使用反向传播求解梯度进而使用梯度下降进行参数更新的过程，而指数函数在求导的时候比较方便.
Softmax不足：
使用指数函数，当输出值非常大的话，计算得到的数值也会变的非常大，数值可能会溢出
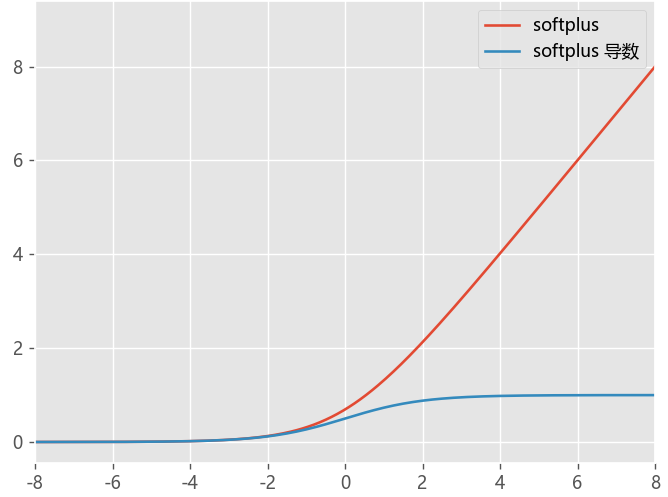
Softplus函数
\[f(f)=In(1+e^x) ~~~~~~~~~ 导数\acute{f(x)}=\frac{e^x}{1+e^x} = \frac{1}{1+e^{-x}}
\]
- Softplus函数可以看作是ReLU****函数的平滑，加了1**是为了保证非负性
def softplus(x):
return np.log(1+np.exp(x))
def softplus_du(x):
return 1.0/(1.0+np.exp(-x))
ReLU型及其改进
ReLU函数
\[f(x)=\begin{cases} x ~~~ x\ge 0
\\0 ~~~ x<0
\end{cases} ~~~~~~~~~ 导数 \acute{f(x)} =\begin{cases} 1 ~~~ x\ge 0
\\0 ~~~ x<0
\end{cases}
\]
ReLU函数是当前最常用的激活函数之一，它的特点是简单、快速，并且在许多情况下表现出色。ReLU函数将负数输入映射到0，将正数输入保留不变，因此在训练过程中可以避免梯度消失的问题。但是ReLU函数在输入为负数时输出为0，这可能导致神经元死亡
# pytorch 框架对应函数： nn.ReLU(inplace=True)
def relu(x):
return np.maximum(x, 0.0)
def relu_du(x):
return 1 if x>=0 else 0
- 计算速度非常快，只需要判断输入是否大于0
- 解决了gradient vanishing问题 (在正区间)，梯度=1
- 具有稀疏性，存在Dead ReLU Problem问题
- 负向输出永远是0，某些神经元可能永远不会被激活，导致永远不会更新
PReLU函数
https://arxiv.org/abs/1502.01852v1
\[f(x)=\begin{cases}x ~~~x>0
\\ \alpha x ~~~ x <0
\end{cases} ~~~~ \alpha 可训练
~~~~~~~导数
\acute{f(x)} =\begin{cases}1 ~~~x>0
\\ \alpha ~~~ x <0
\end{cases} ~~~~ \alpha 可训练
\]
- \(\alpha\) 是可训练参数-其余和LeakyReLU类似
LeakyReLU函数
LeakyReLU函数是ReLU函数的改进版本，它在输入为负数时输出一个小的负数，从而避免了ReLU函数可能导致神经元死亡的问题
\[f(x)=\begin{cases}x ~~~x>0
\\ \lambda x ~~~ x <0
\end{cases} ~~~~\lambda \in (0,1)
~~~~~~~导数
\acute{f(x)} =\begin{cases}1 ~~~x>0
\\ \lambda ~~~ x <0
\end{cases} ~~~~\lambda \in (0,1)
\]
- 通过把 x 的非常小的线性分量给予负输入（0.01x）来调整负值的零梯度
- 扩大 ReLU 函数的范围，负无穷到正无穷
- a值的选择增加了问题难度， 需要较强的人工先验或多次重复训练以确定合适
def LeakyReLU(x, alpha=0.1):
return np.maximum(alpha*x, x)
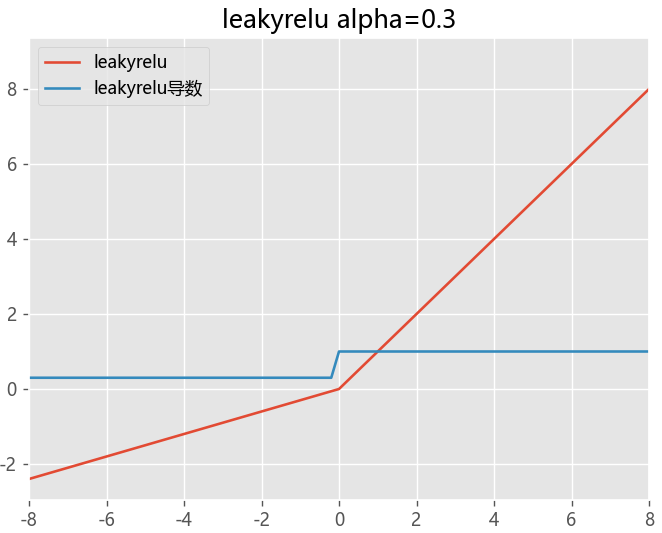
RReLU函数
\[f(x)=\begin{cases}x ~~~x>0
\\ \alpha x ~~~ x <0
\end{cases} ~~~~ \alpha 随机震荡
~~~~~~~导数
\acute{f(x)} =\begin{cases}1 ~~~x>0
\\ \alpha ~~~ x <0
\end{cases} ~~~~ \alpha 随机震荡
\]
def rrelu(x,lower=0.125,upper=0.3):
m = nn.RReLU(lower=0.1, upper=0.3)
return m(x)
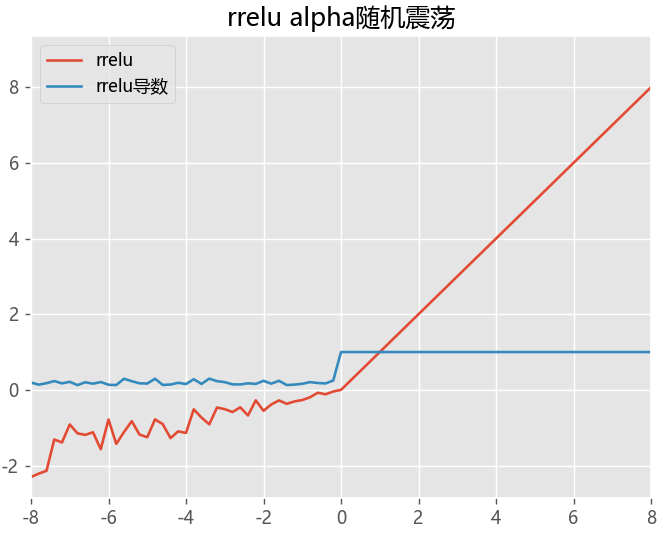
ReLU6函数
\[f(x)= \begin{cases}
6 ~~~~ x>6
\\ x ~~~~x \le 6
\\ 0 ~~~~ x \le 0
\end{cases}
~~~
导数 \acute{f(x)}=
\begin{cases}
0 ~~~~~~ x>6
\\1 ~~~~~~ x \le 6
\\0 ~~~~~~ x \le 0
\end{cases}
\]
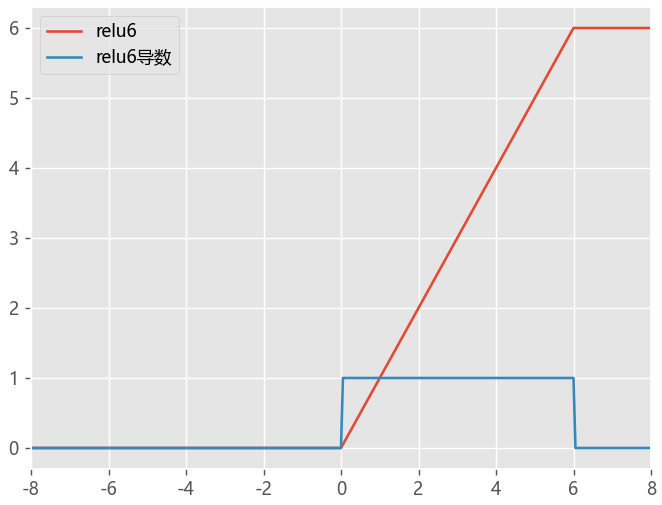
ELU指数线性单元
\[f(x)=\begin{cases}
x , ~~~~~~~~~~~~~~~~ x>0
\\ \alpha (e^x-1),~~x \le 0
\end{cases} ~~~~~~~~~~~~导数
\acute{f(x)}=
\begin{cases} 1 ~~~~~~~~~~~~~~~~~x > 0 \\
\alpha e^x~~~~~~~~~~~~~x \le 0
\end{cases}
\]
ELU 的提出也解决了 ReLU 的问题。与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。
均值激活接近于零可以使学习更快
- ELU 通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向零加速学习
- 没有 Dead ReLU 问题，输出的平均值接近 0，以 0 为中心；
- 可以有效防止死神经元出现。
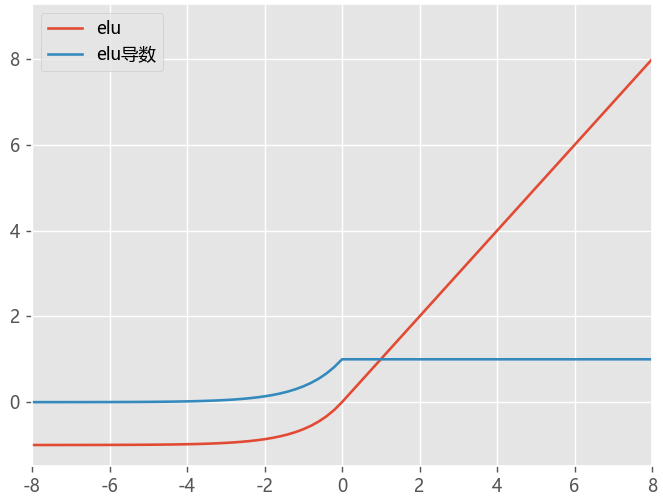
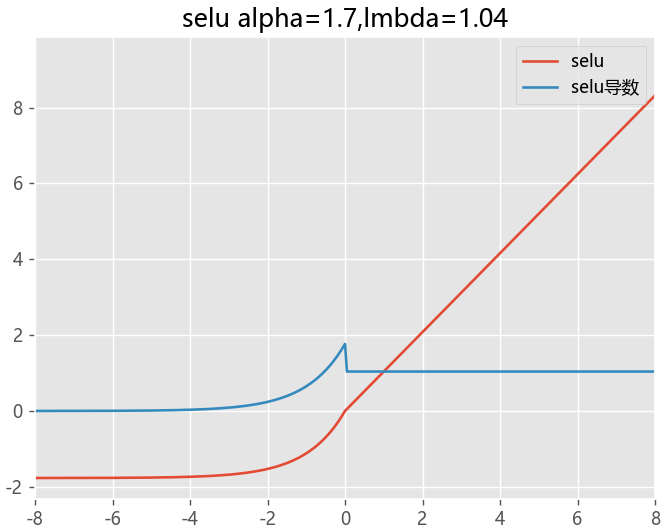
SELU函数
在ELU的基础上新增加系数
\[f(x)= \lambda \begin{cases}
x , ~~~~~~~~~~~~~~~~ x>0
\\ \alpha (e^x-1),~~x \le 0
\end{cases}
~~~
导数 \acute{f(x)}=
\begin{cases}
\lambda ~~~~~~~~~~~~~ x>0
\\
\lambda \alpha e^x ~~~~~~~ x<0
\end{cases}
\]
当其中参数α=1.67 ， λ=1.05时，在网络权重服从正态分布的条件下，各层输出的分布会向标准正态分布靠拢
SELU是给ELU乘上一个系数，该系数大于1
其他类型sigmoid
GELU高斯误差线性单元
\[f(x)= x * sigmoid (1.702x)
\]
也可以近似表示为GELU(x)=0.5∗x∗(1+tanh(√(2/π )∗(x+0.044715x^3) )
- $\sigma $ 为sigmoid 函数
- 详细推导过程参考：https://www.cnblogs.com/makefile/p/activation-function.html
当方差为无穷大，均值为0的时候，GeLU就等价于ReLU了。GELU可以当作为RELU的一种平滑策略。GELU是非线性输出，具有一定的连续性。GELU有一个概率解释，因为它是一个随机正则化器的期望。**
SiLU函数
\[f(x)=x * sigmoid(x) ~~~~~~导数 \acute{f(x)}=sigmoid(x)(1-f(x))+f(x)
\]
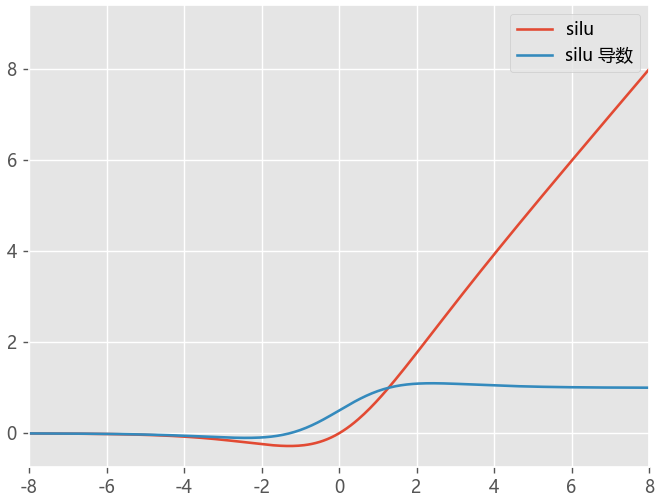
Swish函数
\[f(x)=x * sigmoid(βx)
\]
-
β是个常数或可训练的参数.Swish 具备无上界有下界、平滑、非单调的特性，当β=1时，我们也称作SiLU激活函数。
-
Swish 在深层模型上的效果优于 ReLU
# Swish https://arxiv.org/pdf/1905.02244.pdf
class Swish(nn.Module): #Swish激活函数
@staticmethod
def forward(x, beta = 1): # 此处beta默认定为1
return x * torch.sigmoid(beta*x)
ELU 与 Swish 激活函数（x · σ(βx)）的函数形式和性质非常相像，
一个是固定系数 1.702，另一个是可变系数 β（可以是可训练的参数，也可以是通过搜索来确定的常数），
两者的实际应用表现也相差不大。
其他问题
https://mp.weixin.qq.com/s/QHfSsBEphiTpd7DRoNGO1w
激活函数的选择
- 浅层网络在分类器时，sigmoid函数及其组合通常效果更好。
- 由于梯度消失问题，有时要避免使用 sigmoid和 tanh函数。
- relu函数是一个通用的激活函数，目前在大多数情况下使用。
- 如果神经网络中出现死神经元，那么 prelu函数就是最好的选择。
为什么 relu不是全程可导也能用于基于梯度的学习
数学的角度看 relu在 0点不可导，因为它的左导数和右导数不相等；但在实现时通常会返回左导数或右导数的其中一个
为什么tanh比sigmoid更快
1、梯度消失问题程度,tanh(x)的梯度消失问题比sigmoid要轻
2、以零为中心的影响，Sigmoid 函数作为激活函数是以0.5为中心的
sigmoid和softmax有什么区别
- 二分类问题时 sigmoid和 softmax是一样的，都是求 cross entropy loss，而 softmax可以用于多分类问题。
- 二分类下，sigmoid、softmax两者的数学公式是等价的
- 多个sigmoid与一个softmax都可以进行多分类，softmax中，所有类别之和是1, 类别之间是互斥的
总结
sigmoid将一个real value映射到（0,1）的区间（当然也可以是（-1,1）），这样可以用来做二分类。而softmax把一个k维的real value向量（a1,a2,a3,a4…）映射成一个（b1,b2,b3,b4…）其中bi是一个0-1的常数，然后可以根据bi的大小来进行多分类的任务，如取权重最大的一维。
参考绘图
# example plot for the sigmoid activation function
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
def sigmoid(x):
"""1.0 / (1.0 + exp(-x))"""
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_du(x):
return sigmoid(x) * (1.0 - sigmoid(x))
def tanh(x):
return np.tanh(x)
def tanh_du(x):
return 1.0 - tanh(x)**2
def relu(x):
return np.maximum(x, 0.0)
def relu_du(x):
return 1 if x>=0 else 0
def leakyrelu(x, alpha=0.3):
return np.maximum(alpha*x, x)
def leakyrelu_du(x, alpha=0.3):
return 1 if x>=0 else alpha
def rrelu(x,lower=0.125,upper=0.3):
m = nn.RReLU(lower=0.1, upper=0.3)
random_alpha=np.random.uniform(0.125,0.3)
return x if x>=0 else random_alpha*x
def rrelu_du(x):
random_alpha=np.random.uniform(0.125,0.3)
return 1 if x>=0 else random_alpha
def elu(x,alpha=1):
return x if x>=0 else alpha*(np.exp(x)-1)
def elu_du(x,alpha=1):
return 1 if x>=0 else alpha*(np.exp(x))
def selu(x,alpha=1.7,lmbda=1.04):
return lmbda*x if x>=0 else lmbda*alpha*(np.exp(x)-1)
def selu_du(x,alpha=1.7,lmbda=1.04):
return lmbda if x>=0 else lmbda*alpha*(np.exp(x))
def relu6(x):
return np.clip(x,0,6)
def relu6_du(x):
if x>=6:
return 0
elif 0<x<6:
return 1
else:
return 0
def silu(x,):
return x*sigmoid(x)
def silu_du(x):
return silu(x)+sigmoid(x)*(1-silu(x))
def softmax(x):
return np.exp(x)/np.sum(np.exp(x))
def softmax_du(x):
pass
def softplus(x):
return np.log(1+np.exp(x))
def softplus_du(x):
return 1.0/(1.0+np.exp(-x))
def plotloss(act_func,act_name,title):
plt.style.use('ggplot')
plt.rcParams["font.sans-serif"]=["Microsoft YaHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #正常显示负号
fig = plt.figure()
ax = fig.add_subplot(111)
# 1, define input data
inputs = [x for x in np.arange(-8, 9, 0.05)]
# 2, calculate outputs
plt.xlim(-8, 8)
for act,name in zip(act_func,act_name):
outputs = [act(x) for x in inputs]
plt.plot(inputs, outputs, label=name)
plt.title(title)
plt.legend()
plt.show()
plotloss([softplus,softplus_du],act_name=['softplus','softplus 导数'],title="softplus")
参考绘图2
import torch
import numpy as np
import matplotlib.pylab as plt
import sys
from matplotlib import pyplot as plt
from matplotlib import style
from torch.nn.modules.module import Module
from torch.nn import functional as F
from torch import Tensor
def xyplot(x_vals, y_vals, name):
plt.rcParams['figure.figsize'] = (5, 4)
plt.grid(c='black',linewidth=0.08)
plt.plot(x_vals.detach().numpy(), y_vals.detach().numpy(), label = name, linewidth=1.5)
font = {'family': 'SimHei'}; # 中文字体
plt.legend(loc='upper left',prop=font)
#dark_background, seaborn, ggplot
# plt.style.use("seaborn")
ax = plt.gca()
ax.spines['right'].set_color("none")
ax.spines['top'].set_color("none")
ax.spines['bottom'].set_position(("data",0))
ax.spines['left'].set_position(("data",0))
ax.spines['bottom'].set_linewidth(0.5)
ax.spines['left'].set_linewidth(0.5)
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
# 激活函数以及导函数
def func_(y_func,func_n,save_=None,x_low=-6.0,x_top=6.0):
x = torch.arange(-6.0, 6.0, 0.1, requires_grad=True)
y = y_func(x)
xyplot(x, y, '原函数')
#导数
y.sum().backward()
xyplot(x, x.grad, "导函数")
plt.title(f"{func_n}(x)")
if save_ is not None:
plt.draw()
plt.savefig(f"./{func_n}.jpg")
plt.close()
plt.show()
# 由于我使用的pytorch版本没有Mish函数，所以整了一个
class Mish(Module):
__constants__ = ['beta', 'threshold']
beta: int
threshold: int
def __init__(self, beta: int = 1, threshold: int = 20) -> None:
super(Mish, self).__init__()
self.beta = beta
self.threshold = threshold
def forward(self, input: Tensor) -> Tensor:
return input*torch.tanh(F.softplus(input, self.beta, self.threshold))
def extra_repr(self) -> str:
return 'beta={}, threshold={}'.format(self.beta, self.threshold)
# 没找到Swich，so再整了一个
class Swish(Module):
__constants__ = ['beta']
beta: int
def __init__(self, beta: int = 1) -> None:
super(Swish, self).__init__()
self.beta = beta
def forward(self, input: Tensor) -> Tensor:
return input*torch.sigmoid(input*self.beta)
# RReLU
func_(torch.nn.RReLU(),"RReLU",True)
# ELU
func_(torch.nn.ELU(),"ELU",True)
# SELU
func_(torch.nn.SELU(),"SELU",True)
# CELU
func_(torch.nn.CELU(),"CELU",True)
# GELU
func_(torch.nn.GELU(),"GELU",True)
# ReLU6
func_(torch.nn.ReLU6(),"ReLU6",True)
# Swish
func_(Swish(),"Swish",True)
# Hardswish
func_(torch.nn.Hardswish(),"Hardswish",True)
# SiLU
func_(torch.nn.SiLU(),"SiLU",True)
# Softplus
func_(torch.nn.Softplus(),"Softplus",True)
# Mish
func_(Mish(),"Mish",True)
Softmax
func_(torch.nn.Softmax(dim=0),"Softmax",True)
参考资料
https://www.cnblogs.com/makefile/p/activation-function.html
https://juejin.cn/post/7187663634389663781?searchId=2023110817394434B89A1019EC19C438FA
