非极大值抑制NMS
非极大值抑制NMS
为什么需要NMS
非极大值抑制(Non-Maximum Suppression,NMS),顾名思义就是抑制不是极大值的元素,可以理解为局部最大搜索。在目标检测领域其目的就是要去除冗余的检测框,保留最好的一个。
以目标检测为例,目标检测推理过程中会产生很多检测框 ,其中很多检测框都是检测同一个目标,但最终每个目标只需要一个检测框,NMS选择那个得分最高的检测框 ,再将该候选框与剩余框计算相应的IOU值,当IOU值超过所设定的阈值,即对超过阈值的框进行抑制,抑制的做法是将检测框的得分设置为0,如此一轮过后,在剩下检测框中继续寻找得分最高的,再抑制与之IOU超过阈值的框,直到最后会保留几乎没有重叠的框。这样基本可以做到每个目标只剩下一个检测框。
如何计算NMS
前提: 目标边界框列表及其对应的置信度得分列表,设定阈值,阈值用来删除重叠较大的边界框。
IoU:intersection-over-union,即两个边界框的交集部分除以它们的并集。
非极大值抑制的流程如下:
1. 获取全部bbox信息,根据置信度得分进行排序
2. 按照置信度排序后,记录当前confidence最大的bbox
3. 计算最大confidence对应的bbox 和 剩下的其他的bbox的 IOU
4. 删除IOU 大于阈值的 边界框(bbox) 即 删除重合度较高的边界框
5. 对剩下的候选框 bbox 重复上 排序和计算IOU,删除操作[2][3][4], 直到不能删除为止
区域交并比(IOU)
IOU的原称为Intersection over Union,也就是两个box区域的交集比上并集,很好理解,用于确定两个框的位置像素距离。
常用于计算真实边界框Bgt(数据集的标注)以及预测边界框Bp(模型预测结果)的重叠程度。

思路
- 首先计算两个box左上角点坐标的最大值和右下角坐标的最小值
- 然后计算交集面积
- 最后把交集面积除以对应的并集面积
numpy实现
import numpy as np
def iou(boxes1, boxes2):
"""
Arguments:
boxes1 (Array[N, 4])
boxes2 (Array[M, 4])
"""
# 计算第一组矩形框的面积
area1 = (boxes1[:, 2] - boxes1[:, 0]) * (boxes1[:, 3] - boxes1[:, 1])
# 计算第二组矩形框的面积
area2 = (boxes2[:, 2] - boxes2[:, 0]) * (boxes2[:, 3] - boxes2[:, 1])
# 计算交集的坐标范围
x1 = np.maximum(boxes1[:, 0][:, np.newaxis], boxes2[:, 0])
y1 = np.maximum(boxes1[:, 1][:, np.newaxis], boxes2[:, 1])
x2 = np.minimum(boxes1[:, 2][:, np.newaxis], boxes2[:, 2])
y2 = np.minimum(boxes1[:, 3][:, np.newaxis], boxes2[:, 3])
# 计算交集的面积
inter_area = np.maximum(x2 - x1, 0) * np.maximum(y2 - y1, 0)
# 计算并集的面积
union_area = area1[:, np.newaxis] + area2 - inter_area
# 计算IOU值
iou = inter_area / union_area
return iou
boxes1 = np.array([[10, 10, 50, 50],
[20, 20, 60, 60],
[30, 30, 70, 70]])
boxes2 = np.array([[20, 20, 60, 60],
[30, 30, 70, 70],
[40, 40, 80, 80]])
iou_matrix = iou(boxes1, boxes2)
print(iou_matrix)
[[0.39130435 0.14285714 0.03225806]
[1. 0.39130435 0.14285714]
[0.39130435 1. 0.39130435]]
pytorch实现
from torch import Tensor
import torch
def box_area(boxes: Tensor) -> Tensor:
"""
Computes the area of a set of bounding boxes, which are specified by its
(x1, y1, x2, y2) coordinates.
Arguments:
boxes (Tensor[N, 4]): boxes for which the area will be computed. They
are expected to be in (x1, y1, x2, y2) format
Returns:
area (Tensor[N]): area for each box
"""
return (boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1])
def box_iou(boxes1: Tensor, boxes2: Tensor) -> Tensor:
"""
Return intersection-over-union (Jaccard index) of boxes.
Both sets of boxes are expected to be in (x1, y1, x2, y2) format.
Arguments:
boxes1 (Tensor[N, 4])
boxes2 (Tensor[M, 4])
Returns:
iou (Tensor[N, M]): the NxM matrix containing the pairwise IoU values for every element in boxes1 and boxes2
"""
area1 = box_area(boxes1) # 每个框的面积 (N,)
area2 = box_area(boxes2) # (M,)
lt = torch.max(boxes1[:, None, :2], boxes2[:, :2]) # [N,M,2] # N中一个和M个比较; 所以由N,M 个
rb = torch.min(boxes1[:, None, 2:], boxes2[:, 2:]) # [N,M,2]
wh = (rb - lt).clamp(min=0) # [N,M,2] #小于0的为0 clamp 钳;夹钳;
inter = wh[:, :, 0] * wh[:, :, 1] # [N,M]
iou = inter / (area1[:, None] + area2 - inter)
return iou # NxM, boxes1中每个框和boxes2中每个框的IoU值;
boxes1 = np.array([[10, 10, 50, 50],
[20, 20, 60, 60],
[30, 30, 70, 70]])
boxes2 = np.array([[20, 20, 60, 60],
[30, 30, 70, 70],
[40, 40, 80, 80]])
box1=torch.Tensor(boxes1)
box2=torch.Tensor(boxes2)
iou_matrix = box_iou(box1, box2)
print(iou_matrix)
tensor([[0.3913, 0.1429, 0.0323],
[1.0000, 0.3913, 0.1429],
[0.3913, 1.0000, 0.3913]])
pytorch实现
def box_iou_torch(box1, box2, eps=1e-7):
"""
Calculate intersection-over-union (IoU) of boxes.
Both sets of boxes are expected to be in (x1, y1, x2, y2) format.
Based on https://github.com/pytorch/vision/blob/master/torchvision/ops/boxes.py
Args:
box1 (torch.Tensor): A tensor of shape (N, 4) representing N bounding boxes.
box2 (torch.Tensor): A tensor of shape (M, 4) representing M bounding boxes.
eps (float, optional): A small value to avoid division by zero. Defaults to 1e-7.
Returns:
(torch.Tensor): An NxM tensor containing the pairwise IoU values for every element in box1 and box2.
"""
# inter(N,M) = (rb(N,M,2) - lt(N,M,2)).clamp(0).prod(2)
(a1, a2), (b1, b2) = box1.unsqueeze(1).chunk(2, 2), box2.unsqueeze(0).chunk(2, 2)
inter = (torch.min(a2, b2) - torch.max(a1, b1)).clamp_(0).prod(2)
# IoU = inter / (area1 + area2 - inter)
return inter / ((a2 - a1).prod(2) + (b2 - b1).prod(2) - inter + eps)
boxes1 = np.array([[10, 10, 50, 50],
[20, 20, 60, 60],
[30, 30, 70, 70]])
boxes2 = np.array([[20, 20, 60, 60],
[30, 30, 70, 70],
[40, 40, 80, 80]])
box1=torch.Tensor(boxes1)
box2=torch.Tensor(boxes2)
res=box_iou_torch(box1,box2)
tensor([[0.3913, 0.1429, 0.0323],
[1.0000, 0.3913, 0.1429],
[0.3913, 1.0000, 0.3913]])
非极大值抑制NMS
numpy实现
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
def py_cpu_nms(dets, thresh):
# dets:(m,5) thresh:scaler
x1 = dets[:,0]
y1 = dets[:,1]
x2 = dets[:,2]
y2 = dets[:,3]
bboxs = dets[:,:4]
scores = dets[:,4]
areas = (y2-y1) * (x2-x1) # 计算每个box面积
index = scores.argsort()[::-1] # scores 排序
keep_bboxs = []
keep_scors = []
while index.size > 0:
i = index[0] # 已scores最大为基准
keep_bboxs.append(bboxs[i]) # 要返回的结果
keep_scors.append(dets[i])
x11 = np.maximum(x1[i], x1[index[1:]])
y11 = np.maximum(y1[i], y1[index[1:]])
x22 = np.minimum(x2[i], x2[index[1:]])
y22 = np.minimum(y2[i], y2[index[1:]])
w = np.maximum(0, x22-x11) # the weights of overlap
h = np.maximum(0, y22-y11) # the height of overlap
overlaps = w*h # 依次,计算交集
ious = overlaps / (areas[i]+areas[index[1:]] - overlaps) # 计算交并比
idx = np.where(ious<=thresh)[0] # 删除IOU大于阈值的,返回过滤剩下bbox
# 过滤iou大于阈值,
# 因为没有计算与自身的IOU,所以索引相差1
index = index[idx+1]
return keep_bboxs,keep_scors
def plot_bbox(dets, color='k',title=None):
fig=plt.figure()
axs=fig.add_subplot(111)
x1 = dets[:,0]
y1 = dets[:,1]
x2 = dets[:,2]
y2 = dets[:,3]
# print(x1.shape) # (6,)
# 通过绘制直线的方式,绘制矩形
axs.plot([x1,x2], [y1,y1], color)
axs.plot([x1,x1], [y1,y2], color)
axs.plot([x1,x2], [y2,y2], color)
axs.plot([x2,x2], [y1,y2], color)
if title:
plt.title(title)
plt.show()
boxes=np.array([[100,100,210,210,0.72],
[250,250,420,420,0.8],
[220,220,320,330,0.92],
[100,100,210,210,0.72],
[230,240,325,330,0.81],
[220,230,315,340,0.9]])
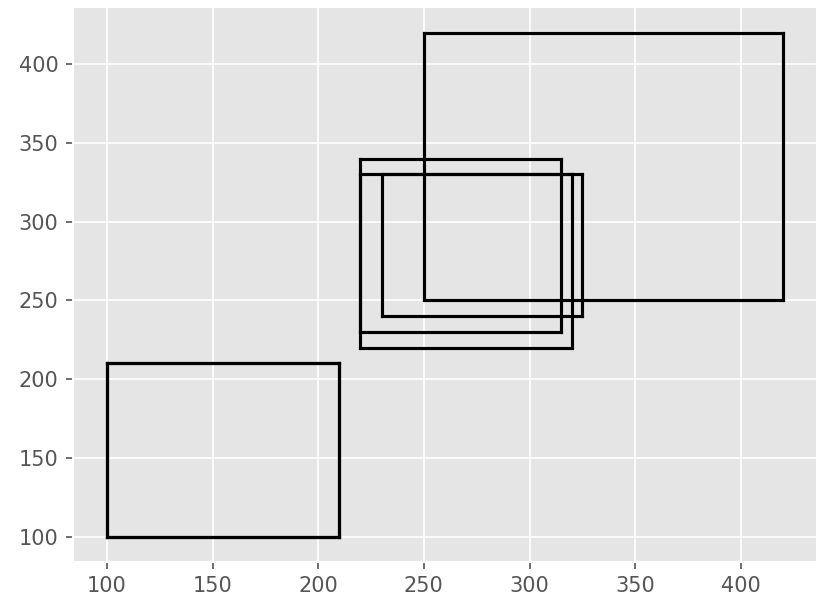
plot_bbox(boxes,'k') # before nms
keep_bboxs,keep_scors = py_cpu_nms(boxes, thresh=0.6)
plot_bbox(np.array(keep_bboxs), 'r') # after nms
pytorch实现
def nms(boxes: Tensor, scores: Tensor, iou_threshold: float):
"""
:param boxes: [N, 4], 此处传进来的框,是经过筛选(NMS之前选取过得分TopK)之后, 在传入之前处理好的;
:param scores: [N]
:param iou_threshold: 0.7
:return:
"""
keep = [] # 最终保留的结果, 在boxes中对应的索引;
idxs = scores.argsort() # 值从小到大的 索引
while idxs.numel() > 0: # 循环直到null; numel(): 数组元素个数
# 得分最大框对应的索引, 以及对应的坐标
max_score_index = idxs[-1]
max_score_box = boxes[max_score_index][None, :] # [1, 4]
keep.append(max_score_index)
if idxs.size(0) == 1: # 就剩余一个框了;
break
idxs = idxs[:-1] # 将得分最大框 从索引中删除; 剩余索引对应的框 和 得分最大框 计算IoU;
other_boxes = boxes[idxs] # [?, 4]
ious = box_iou(max_score_box, other_boxes) # 一个框和其余框比较 1XM
idxs = idxs[ious[0] <= iou_threshold]
keep = idxs.new(keep) # Tensor
return keep
参考资料
https://zhuanlan.zhihu.com/p/54709759
https://blog.csdn.net/weixin_44979150/article/details/122974977
https://blog.csdn.net/weixin_41311686/article/details/128008640 代码和图解




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· winform 绘制太阳,地球,月球 运作规律
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人