IoU,GIoU,DIoU,CloU损失函数

IoU,GIoU,DIoU,CloU损失函数

目录

• IoU,GIoU,DIoU,CloU损失函数
  • IoU Loss 交并比
    • numpy实现
    • torch实现
    • 优缺点
  • GIoU Loss
    • numpy实现
    • torch实现
    • 优缺点
  • DIoU Loss
    • numpy实现
    • 优缺点
  • CIoU Loss

图例介绍

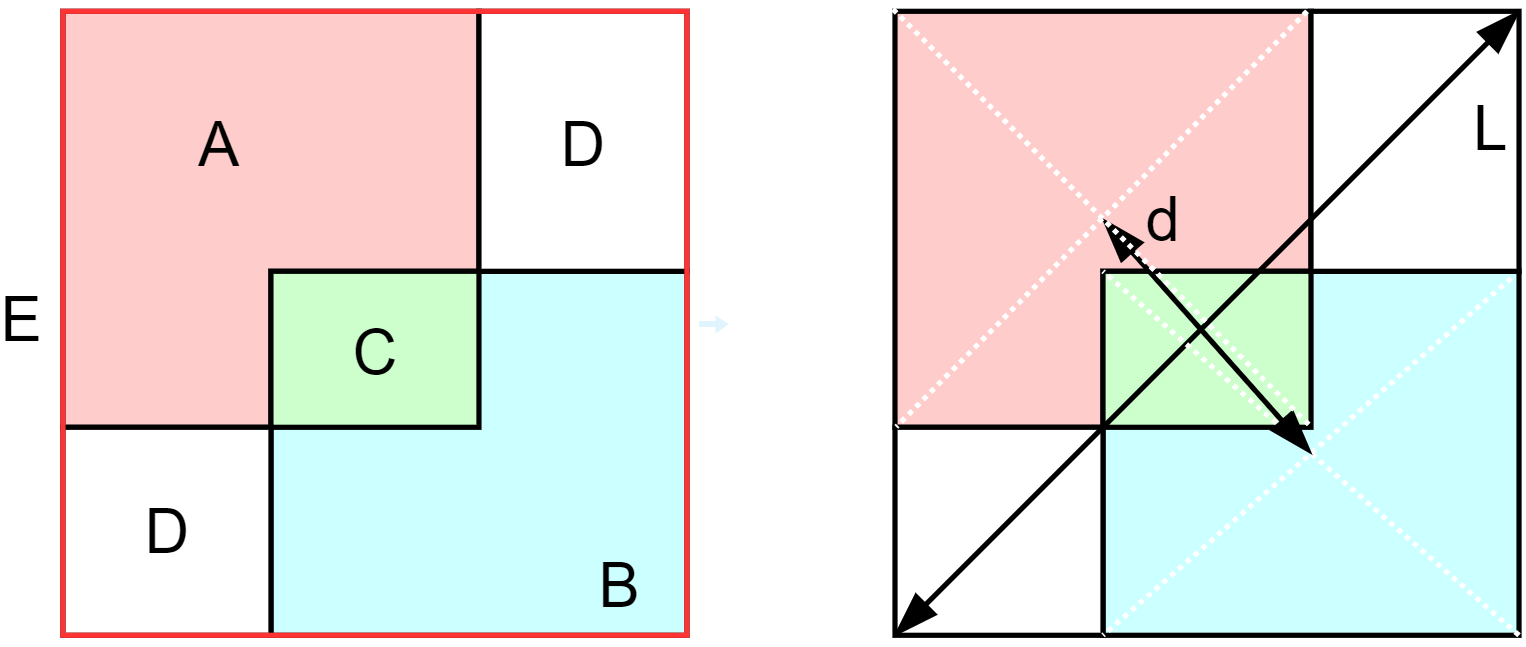
A: 目标框覆盖的矩形面积（粉色区域表示，包含被C掩盖掉的区域）
B: 预测框覆盖的矩形面积（蓝色区域表示，包含被C掩盖掉的区域）
C: A和B重叠部分的矩形面积（C是A和B的交集）
D: 图1中两块白色区域面积之和（A和B最小外接矩形的面积 减去 A和B的并集面积）
E: A和B最小外接矩形的面积（图1的总面积，E=A+B-C+D）
d: A中心点到B中心点的欧式距离
L: A和B最小外接矩形的对角线距离

IoU Loss 交并比

IoU就是我们所说的交并比，是目标检测中最常用的指标，在anchor-based的方法中，他的作用不仅用来确定正样本和负样本，还可以用来评价输出框（predict box）和ground-truth的距离。

\[IoU=\frac{A\cap B}{A\sqcup B} = \frac{C}{A+B-C} \]

\[loss= 1- IoU \]

numpy实现

单维度box实现

def IoU(box1, box2):
    b1_x1, b1_y1, b1_x2, b1_y2 = box1
    b2_x1, b2_y1, b2_x2, b2_y2 = box2
    
    xx1 = np.maximum(b1_x1, b2_x1)
    yy1 = np.maximum(b1_y1, b2_y1)
    xx2 = np.minimum(b1_x2, b2_x2)
    yy2 = np.minimum(b1_y2, b2_y2)
    
    w = np.maximum(0.0, yy2 - yy1)
    h = np.maximum(0.0, xx2 - xx1)
 	
    inter = w * h
    IoU = inter/((b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter)
    print("IoU: ", IoU)
    return IoU
box1 = np.array([100, 100, 210, 210])
box2 = np.array([150, 150, 230, 220])
IoU(box1, box2)

多维度box实现

import numpy as np
def box_iou(boxes1, boxes2):
    """计算两个锚框或边界框列表中成对的交并比"""
    # boxes1,boxes2,areas1,areas2的形状:
    # boxes1：(boxes1的数量,4),
    # boxes2：(boxes2的数量,4),
    box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1]))

    # areas1：(boxes1的数量,),
    # areas2：(boxes2的数量,)
    areas1 = box_area(boxes1)
    areas2 = box_area(boxes2)

    # inter_upperlefts,inter_lowerrights,inters的形状:
    # (boxes1的数量,boxes2的数量,2)
    inter_upperlefts = np.maximum(boxes1[:, None, :2], boxes2[:, :2])
    inter_lowerrights = np.minimum(boxes1[:, None, 2:], boxes2[:, 2:])
    inters = (inter_lowerrights - inter_upperlefts).clip(min=0)
    # inter_areasandunion_areas的形状:(boxes1的数量,boxes2的数量)
    inter_areas = inters[:, :, 0] * inters[:, :, 1]
    union_areas = areas1[:, None] + areas2 - inter_areas
    IOU= inter_areas / union_areas
    return IOU
 

if __name__ == "__main__":
    box1 = np.array([[100, 100, 210, 210]])
    box2 = np.array([[150, 150, 230, 220]])
    res=box_iou(box1, box2)
    print(res)

torch实现

import numpy as np
import torch

def box_iou(boxes1, boxes2):
    """计算两个锚框或边界框列表中成对的交并比"""
    # boxes1,boxes2,areas1,areas2的形状:
    # boxes1：(boxes1的数量,4),
    # boxes2：(boxes2的数量,4),
    
    box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1]))
    
    # areas1：(boxes1的数量,),
    # areas2：(boxes2的数量,)
    areas1 = box_area(boxes1)
    areas2 = box_area(boxes2)
    # inter_upperlefts,inter_lowerrights,inters的形状:
    # (boxes1的数量,boxes2的数量,2)
    inter_upperlefts = torch.max(boxes1[:, None, :2], boxes2[:, :2])
    inter_lowerrights = torch.min(boxes1[:, None, 2:], boxes2[:, 2:])
    inters = (inter_lowerrights - inter_upperlefts).clamp(min=0)
    # inter_areasandunion_areas的形状:(boxes1的数量,boxes2的数量)
    inter_areas = inters[:, :, 0] * inters[:, :, 1]
    union_areas = areas1[:, None] + areas2 - inter_areas
    return inter_areas / union_areas

if __name__ == "__main__":
    box1 = np.array([[100, 100, 210, 210]])
    box2 = np.array([[150, 150, 230, 220]])
    res=box_iou(torch.from_numpy(box1), torch.from_numpy(box2))
    print(res)
    

参考资料 https://zh.d2l.ai/chapter_computer-vision/anchor.html#iou

优缺点

优点
1.可以反映预测检测框与真实检测框的检测效果。
2.尺度不变性,也就是对尺度不敏感(scale invariant) 在regression任务中，判断predict box和gt的距离最直接的指标就是IoU

缺点
1. 如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小（重合度）。 无法衡量完全不相交的两个框
同时因为loss=0，没有梯度回传，无法进行学习训练。                          

2.IoU无法精确的反映两者的重合度大小。          两个不同形状的预测框可能产生相同的loss
如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

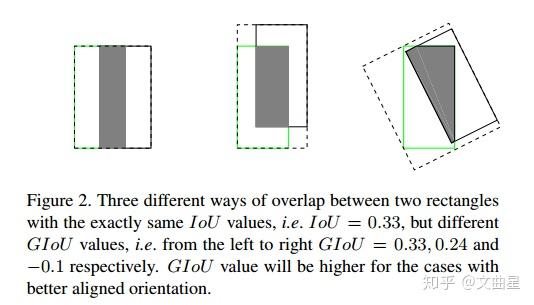
GIoU Loss

先计算两个框的最小闭包区域面积Ac 即 预测框和真实框的最小外接矩形, 求出最小外接矩形减去两个预测框union的面积

(通俗理解：同时包含了预测框和真实框的最小框的面积)

\[GIoU=IoU- \frac{\left | A_{c} -U \right | }{ A_{c} }= \frac{C}{A+B-C} -\frac{D}{E} \]

\[loss= 1- GIoU \]

与IoU相似，GIoU也是一种距离度量 GIoU的范围是[-1, 1] GIOU Loss的范围在[0, 2]

GIoU是IoU的下界，在两个框无限重合的情况下，IoU=GIoU=1

与IoU只关注重叠区域不同，GIoU不仅关注重叠区域，还关注其他的非重合区域

numpy实现

def GIoU(box1, box2):
    b1_x1, b1_y1, b1_x2, b1_y2 = box1
    b2_x1, b2_y1, b2_x2, b2_y2 = box2
    
    # IOU
    xx1 = np.maximum(b1_x1, b2_x1)
    yy1 = np.maximum(b1_y1, b2_y1)
    xx2 = np.minimum(b1_x2, b2_x2)
    yy2 = np.minimum(b1_y2, b2_y2)
    inter_w = np.maximum(0.0, yy2 - yy1)
    inter_h = np.maximum(0.0, xx2 - xx1)
    inter = inter_w * inter_h
    Union = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter
 	
    # GIOU
    C_xx1 = np.minimum(b1_x1, b2_x1)
    C_yy1 = np.minimum(b1_y1, b2_y1)
    C_xx2 = np.maximum(b1_x2, b2_x2)
    C_yy2 = np.maximum(b1_y2, b2_y2)
    C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)
    # 计算IOU
    IOU = inter / Union
    GIOU = IOU - abs((C_area-Union)/C_area)
    print("GIOU:", GIOU)
 
if __name__ == "__main__":
    box1 = np.array([100, 100, 210, 210])
    box2 = np.array([150, 150, 230, 220])
    GIoU(box1, box2)

def box_giou(boxes1, boxes2):
    """计算两个锚框或边界框列表中成对的交并比"""
    # boxes1,boxes2,areas1,areas2的形状:
    # boxes1：(boxes1的数量,4),
    # boxes2：(boxes2的数量,4),
    box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1]))
    # areas1：(boxes1的数量,),
    # areas2：(boxes2的数量,)
    areas1 = box_area(boxes1)    
    areas2 = box_area(boxes2)   

    # inter_upperlefts,inter_lowerrights,inters的形状:
    # (boxes1的数量,boxes2的数量,2)
    inter_upperlefts = np.maximum(boxes1[:, None, :2], boxes2[:, :2])
    inter_lowerrights = np.minimum(boxes1[:, None, 2:], boxes2[:, 2:])
        
    inters = (inter_lowerrights - inter_upperlefts).clip(min=0)    # 截取函数最小=0 
    # inter_areasandunion_areas的形状:(boxes1的数量,boxes2的数量)
    inter_areas = inters[:, :, 0] * inters[:, :, 1]

    union_areas = areas1[:, None] + areas2 - inter_areas
    IOU= inter_areas / union_areas
    # GIOU
    out_upperlefts = np.minimum(boxes1[:, None, :2], boxes2[:, :2])
    out_lowerrights = np.maximum(boxes1[:, None, 2:], boxes2[:, 2:])
    
    outs = (out_lowerrights - out_upperlefts).clip(min=0)    # 截取函数最小=0 
    outs_areas = outs[:, :, 0] * outs[:, :, 1]
    GIOU = IOU - abs((outs_areas-union_areas)/outs_areas)
    print("GIOU:", GIOU)
    return  GIOU

torch实现

    
def box_giou(boxes1, boxes2):
    """计算两个锚框或边界框列表中成对的交并比"""
    # boxes1,boxes2,areas1,areas2的形状:
    # boxes1：(boxes1的数量,4),
    # boxes2：(boxes2的数量,4),
    box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1]))
    # areas1：(boxes1的数量,),
    # areas2：(boxes2的数量,)
    areas1 = box_area(boxes1)    
    areas2 = box_area(boxes2)   

    # inter_upperlefts,inter_lowerrights,inters的形状:
    # (boxes1的数量,boxes2的数量,2)
    inter_upperlefts = torch.max(boxes1[:, None, :2], boxes2[:, :2])
    inter_lowerrights = torch.min(boxes1[:, None, 2:], boxes2[:, 2:])
        
    inters = (inter_lowerrights - inter_upperlefts).clip(min=0)    # 截取函数最小=0 
    # inter_areasandunion_areas的形状:(boxes1的数量,boxes2的数量)
    inter_areas = inters[:, :, 0] * inters[:, :, 1]

    union_areas = areas1[:, None] + areas2 - inter_areas
    IOU= inter_areas / union_areas
    # GIOU
    out_upperlefts = torch.min(boxes1[:, None, :2], boxes2[:, :2])
    out_lowerrights = torch.max(boxes1[:, None, 2:], boxes2[:, 2:])
    
    outs = (out_lowerrights - out_upperlefts).clip(min=0)    # 截取函数最小=0 
    outs_areas = outs[:, :, 0] * outs[:, :, 1]
    GIOU = IOU - abs((outs_areas-union_areas)/outs_areas)
    print("GIOU:", GIOU)
    return  GIOU

优缺点

优点
GIOU Loss解决了IOU Loss在不相交情况的问题
GIoU考虑到了 IoU 没有考虑到的预测框和真实框的非重叠区域

缺点
无法衡量有包含关系时的框回归损失, 当预测框和真实框完全重合时（预测框在真实框的内部）GIOU=IOU
GIOU仍然严重依赖IOU，因此在两个垂直方向，误差很大，基本很难收敛,不稳定

DIoU Loss

针对上述GIOU的两个问题，将GIOU中引入最小外接框来最大化重叠面积的惩罚项修改成最小化两个BBox中心点的标准化距离从而加速损失的收敛过程

DIoU要比GIou更加符合目标框回归的机制，将目标与anchor之间的距离，重叠率以及尺度都考虑进去，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。

\[DIoU= IoU- \frac{\rho^{2}(b,b^{gt}) }{ c^{2} } =\frac{C}{A+B-C} -\frac{d}{L} \]

其中， $$b$$ ， 分别代表了预测框和真实框的中心点，且 $$b^{gt}$$ 代表的是计算两个中心点间的欧式距离。 $$\rho$$ 代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。

numpy实现

def DIoU(box1, box2):
    b1_x1, b1_y1, b1_x2, b1_y2 = box1
    b2_x1, b2_y1, b2_x2, b2_y2 = box2
    
    # IOU
    xx1 = np.maximum(b1_x1, b2_x1)
    yy1 = np.maximum(b1_y1, b2_y1)
    xx2 = np.minimum(b1_x2, b2_x2)
    yy2 = np.minimum(b1_y2, b2_y2)
    inter_w = np.maximum(0.0, xx2 - xx1)
    inter_h = np.maximum(0.0, yy2 - yy1)
    inter = inter_w * inter_h
    Union = (b1_x2 - b1_x1)*(b1_y2 - b1_y1) + (b2_x2 - b2_x1)*(b2_y2 - b2_y1) - inter
 
    # DISTANCE
    C_xx1 = np.minimum(b1_x1, b2_x1)
    C_yy1 = np.minimum(b1_y1, b2_y1)
    C_xx2 = np.maximum(b1_x2, b2_x2)
    C_yy2 = np.maximum(b1_y2, b2_y2)
    C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)
 
    center_b_x = (b1_x1+b1_x2)/2
    center_b_y = (b1_y1+b1_y2)/2
    center_gtb_x = (b2_x1+b2_x2)/2
    center_gtb_y = (b2_y1+b2_y2)/2
 
    center_distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2
	c_distance = (C_xx2 - C_xx1)**2 + (C_yy2 - C_yy1)**2
	
    IOU = inter/Union
    DIOU = IOU - center_distance /c_distance
    print("DIOU:", DIOU)
 
if __name__ == "__main__":
    box1 = np.array([100, 100, 210, 210])
    box2 = np.array([150, 150, 230, 220])
    DIoU(box1, box2)

import numpy as np

def DIoU(boxes1, boxes2):
    """计算两个锚框或边界框列表中成对的交并比"""
    # boxes1,boxes2,areas1,areas2的形状:
    # boxes1：(boxes1的数量,4),
    # boxes2：(boxes2的数量,4),
    box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1]))
    # areas1：(boxes1的数量,),
    # areas2：(boxes2的数量,)
    areas1 = box_area(boxes1)    
    areas2 = box_area(boxes2)   

    # inter_upperlefts,inter_lowerrights,inters的形状:
    # (boxes1的数量,boxes2的数量,2)    
    inter_upperlefts = np.maximum(boxes1[:, None, :2], boxes2[:, :2])
    inter_lowerrights = np.minimum(boxes1[:, None, 2:], boxes2[:, 2:])
        
    inters = (inter_lowerrights - inter_upperlefts).clip(min=0)    # 不想交为负值,截取函数最小=0
    # inter_areasandunion_areas的形状:(boxes1的数量,boxes2的数量)
    inter_areas = inters[:, :, 0] * inters[:, :, 1]

    union_areas = areas1[:, None] + areas2 - inter_areas
    IOU= inter_areas / union_areas
 
    # 中心坐标
    center_b_x = (boxes1[:,0]+boxes1[:,2])/2
    center_b_y = (boxes1[:,1]+boxes1[:,3])/2
    center_gtb_x = (boxes2[:,0]+boxes2[:,2])/2
    center_gtb_y = (boxes2[:,1]+boxes2[:,3])/2
    # 中心距离
    center_distance= (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2
    
    # 45对角距离
    out_upperleft= np.minimum(boxes1[:, :2], boxes2[:, :2])
    out_lowerright= np.maximum(boxes1[:, 2:], boxes2[:, 2:])
    
    out_union = (out_lowerright - out_upperleft).clip(min=0)
    c_distance = out_union[:,  0] **2  +  out_union[:,  1]**2
    
    DIOU = IOU - center_distance /c_distance
    return DIOU

 
if __name__ == "__main__":
    box1 = np.array([[100, 100, 210, 210]])
    box2 = np.array([[150, 150, 230, 230]])
    DIoU(box1, box2)

优缺点

优点：
1.DIOU与IOU、GIOU一样具有尺度不变性;
2.与GIoU loss类似 在与目标框不重叠时，仍然可以为边界框提供移动方向
3.DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多
4.包含两个框在水平方向和垂直方向,DIoU损失可以使回归非常快, 依赖于预测框和真实框中心点的距离
5.DIoU还可以替换普通的IoU评价策略，应用于NMS中，使得NMS得到的结果更加合理和有效

CIoU Loss

虽然DIOU能够直接最小化预测框和真实框的中心点距离加速收敛，但是Bounding box的回归还有一个重要的因素宽高比暂未考虑。

bbox回归三要素中的长宽比还没被考虑到计算中

\[DIoU= IoU- \frac{\rho^{2}(b,b^{gt}) }{ c^{2} } -\alpha \vartheta = \frac{C}{A+B-C} -\frac{d}{L} -\alpha \vartheta \]

\[\upsilon = \frac{4}{\pi^2} (arctan\frac{w^{gt}}{h^{gt}} - arctan\frac{w^{pred}}{h^{pred}} )^2 \]

\[\alpha $$是权重系数，在论文里有相关计算， $$\vartheta$$ 是两个框长宽比指标的相似性计算，意思是在IOU值和中心点距离值相同时，两个框的长宽比指标越相似，说明预测框与目标框的对比效果越好。 #### numpy实现 ```python def CIoU(box1, box2): b1_x1, b1_y1, b1_x2, b1_y2 = box1 b2_x1, b2_y1, b2_x2, b2_y2 = box2 # IOU xx1 = np.maximum(b1_x1, b2_x1) yy1 = np.maximum(b1_y1, b2_y1) xx2 = np.minimum(b1_x2, b2_x2) yy2 = np.minimum(b1_y2, b2_y2) inter_w = np.maximum(0.0, xx2 - xx1) inter_h = np.maximum(0.0, yy2 - yy1) inter = inter_w*inter_h Union = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter IOU = inter/Union C_xx1 = np.minimum(b1_x1, b2_x1) C_yy1 = np.minimum(b1_y1, b2_y1) C_xx2 = np.maximum(b1_x2, b2_x2) C_yy2 = np.maximum(b1_y2, b2_y2) # DISTANCE center_b_x = (b1_x1 + b1_x2)/2 center_b_y = (b1_y1 + b1_y2)/2 center_gtb_x = (b2_x1 + b2_x2)/2 center_gtb_y = (b2_y1 + b2_y2)/2 C_area = (C_xx2-C_xx1)*(C_yy2-C_yy1) Distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2 Distance_area = Distance/C_area**2 # aspect ratio pred_w = b1_y2 - b1_y1 pred_h = b1_x2 - b1_x1 gt_w = b2_y2 - b2_y1 gt_h = b2_x2 - b2_x1 v = (4/(np.pi)**2)*(np.arctan(gt_w/gt_h) - np.arctan(pred_w/pred_h))**2 alpha = v/((1-IOU) + v) CIOU = IOU - Distance_area - alpha*v print("CIOU:", CIOU) if __name__ == "__main__": box1 = np.array([100, 100, 210, 210]) box2 = np.array([150, 150, 230, 220]) CIoU(box1, box2) ``` ```python import numpy as np def DIoU(boxes1, boxes2): """计算两个锚框或边界框列表中成对的交并比""" # boxes1,boxes2,areas1,areas2的形状: # boxes1：(boxes1的数量,4), # boxes2：(boxes2的数量,4), box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1])) # areas1：(boxes1的数量,), # areas2：(boxes2的数量,) areas1 = box_area(boxes1) areas2 = box_area(boxes2) # inter_upperlefts,inter_lowerrights,inters的形状: # (boxes1的数量,boxes2的数量,2) inter_upperlefts = np.maximum(boxes1[:, None, :2], boxes2[:, :2]) inter_lowerrights = np.minimum(boxes1[:, None, 2:], boxes2[:, 2:]) inters = (inter_lowerrights - inter_upperlefts).clip(min=0) # 不想交为负值,截取函数最小=0 # inter_areasandunion_areas的形状:(boxes1的数量,boxes2的数量) inter_areas = inters[:, :, 0] * inters[:, :, 1] union_areas = areas1[:, None] + areas2 - inter_areas IOU= inter_areas / union_areas # 中心坐标 center_b_x = (boxes1[:,0]+boxes1[:,2])/2 center_b_y = (boxes1[:,1]+boxes1[:,3])/2 center_gtb_x = (boxes2[:,0]+boxes2[:,2])/2 center_gtb_y = (boxes2[:,1]+boxes2[:,3])/2 # 中心距离 center_distance= (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2 # 45对角距离 out_upperleft= np.minimum(boxes1[:, :2], boxes2[:, :2]) out_lowerright= np.maximum(boxes1[:, 2:], boxes2[:, 2:]) out_union = (out_lowerright - out_upperleft).clip(min=0) c_distance = out_union[:, 0] **2 + out_union[:, 1]**2 DIOU = IOU - center_distance /c_distance print("DIOU", DIOU) pred_w = box1[:,3] - box1[:,1] pred_h = box1[:,2] - box1[:,0] gt_w = box2[:,3] - box2[:,1] gt_h = box2[:,2] - box2[:,0] v = (4/(np.pi)**2)*(np.arctan(gt_w/gt_h) - np.arctan(pred_w/pred_h))**2 alpha = v/((1-IOU) + v) CIOU = DIOU - alpha*v print("DIOU",DIOU) print("alpha*v ",alpha*v ) print("CIOU", CIOU) return CIOU if __name__ == "__main__": box1 = np.array([[100, 100, 210, 210]]) box2 = np.array([[150, 150, 240, 200]]) DIoU(box1, box2) ``` #### 优缺点 ``` 优点： 1.添加了长宽比的惩罚项，使得评估更加准确。 缺点： CIOU Loss涉及到反三角函数 ``` ### EIOU Loss <img src="https://img-blog.csdnimg.cn/8d31896373b04c3ab121cdbc9582fa1a.png#pic_center" alt="img" style="zoom:50%;" /> EIoU在CIoU的基础上将长宽比拆开，明确地衡量了三个几何因素的差异，即重叠区域、中心点和边长，同时引入Fcoal loss解决了难易样本不平衡的问题。 EIOU的惩罚项是在CIOU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和锚框的长和宽，该损失函数包含三个部分：重叠损失，中心距离损失，宽高损失 \]

DIoU= IoU- \frac{\rho^{2}(b,b) }{ c^{2} } -\frac{\rho^2(w,w)}{C_{w}^{2} } -\frac{\rho^2(h,h)}{C_{h}^{2} }

\[ 其中，**wc**和**hc**是预测边界框与真实边界框的最小外接矩形的宽度和高度。**p**是两点之间的欧氏距离。 ### 总结 IOU Loss： 考虑了重叠面积，归一化坐标尺度； GIOU Loss：考虑了重叠面积，基于IOU解决边界框不相交时loss等于0的问题； DIOU Loss：考虑了重叠面积和中心点距离，基于IOU解决GIOU收敛慢的问题； CIOU Loss：考虑了重叠面积、中心点距离、纵横比，基于DIOU提升回归精确度； EIOU Loss：考虑了重叠面积，中心点距离、长宽边长真实差，基于CIOU解决了纵横比的模糊定义，并添加Focal Loss解决BBox回归中的样本不平衡问题。 ### 参考资料 [损失函数：IoU、GIoU、DIoU、CIoU、EIoU、alpha IoU、SIoU、WIoU超详细精讲及Pytorch实现](https://blog.csdn.net/weixin_43334693/article/details/131304963?utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_baidulandingword~default-1-131304963-blog-123325828.235^v38^pc_relevant_anti_vip_base&spm=1001.2101.3001.4242.2&utm_relevant_index=4) [详解IoU、GIoU、DIoU、CIoU、EIoU和DIoU-NMS](https://blog.csdn.net/qq_41542989/article/details/123846530) [IOU、GIOU、DIOU、CIOU的学习及代码实现](https://blog.csdn.net/To_be_little/article/details/124674924?utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_baidulandingword~default-0-124674924-blog-122482345.235^v38^pc_relevant_anti_vip_base&spm=1001.2101.3001.4242.1&utm_relevant_index=3) numpy代码实现和可视化 https://zhuanlan.zhihu.com/p/504735862 https://zhuanlan.zhihu.com/p/94799295 https://juejin.cn/post/7040806104905252894?searchId=20231107172239D59BB9C80EBDA3108595 \]