K-Means聚类
K-Means聚类
聚类,简单来说,就是将一个庞杂数据集中具有相似特征的数据自动归类到一起,称为一个簇,簇内的对象越相似,聚类的效果越好。它是一种无监督的学习(Unsupervised Learning)方法,不需要预先标注好的训练集。聚类与分类最大的区别就是分类的目标事先已知,例如猫狗识别,你在分类之前已经预先知道要将它分为猫、狗两个种类;而在你聚类之前,你对你的目标是未知的,同样以动物为例,对于一个动物集来说,你并不清楚这个数据集内部有多少种类的动物,你能做的只是利用聚类方法将它自动按照特征分为多类,然后人为给出这个聚类结果的定义(即簇识别)。例如,你将一个动物集分为了三簇(类),然后通过观察这三类动物的特征,你为每一个簇起一个名字,如大象、狗、猫等,这就是聚类的基本思想。
聚类与分类算法的最大区别在于, 分类的目标类别已知, 而聚类的目标类别是未知的.
基于中心的聚类
K-Means
K-Means 是发现给定数据集的 K 个簇的聚类算法, 之所以称之为 K-均值 是因为它可以发现 K 个不同的簇, 且每个簇的中心采用簇中所含值的均值计算而成.
簇个数 K 是用户指定的, 每一个簇通过其质心(centroid), 即簇中所有点的中心来描述
优点:
- 属于无监督学习,无须准备训练集
- 原理简单,实现起来较为容易
- 结果可解释性较好
- 速度非常快,只是计算数据点和质心点之间的距离
缺点:
- 需手动设置k值。 在算法开始预测之前,我们需要手动设置k值,即估计数据大概的类别个数,不合理的k值会使结果缺乏解释性
- 对于异常点、离群点敏感
- 容易受初始质心的影响;算法简单,容易实现;算法聚类时,容易产生空簇;算法可能收敛到局部最小值
- 在大规模数据集上收敛较慢
实现过程
1. 首先选择 K 个随机的点,称为 聚类中心 (初始质心)
2. 簇分配: 对于数据集中的 每一个数据,按照 距离 K个中心点的距离,将其与距离最近的中心点 关联起来,与 同一个中心点 关联的所有点聚成一类。
3. 移动聚类中心:计算每一个组的平均值,将该组 所关联的中心点 移动到 该组平均值的位置。
4. 重复步骤2-3直至中心点不再变化。
K-Means++
K-Means++,算法受初始质心影响较小;表现上,往往优于 K-Means 算法;与 K-Means算法不同仅在于初始质心的选择方式不同
在选择初始质心上,进行优化:
1.从样本中选择 1 个点作为初始质心(完全随机)
2.对于任意一个非质心样本 x,计算x与现有最近质心距离 D(x)
3.基于距离计算概率,来选择下一个质心 x,选择距离当前质心远的点作为质心
4.重复步骤 2 与 3 ,直到选择 k 个质心为止。
numpy实现
import numpy as np
class KMeans:
def __init__(self, k=2, max_iterations=100):
self.k = k
self.max_iterations = max_iterations
def fit(self, X):
# 随机初始化聚类质心
self.centroids = X[np.random.choice(range(len(X)), size=self.k, replace=False)]
for i in range(self.max_iterations):
# 将每个数据点分配给最近的质心
distances = np.sqrt(((X - self.centroids[:, np.newaxis])**2).sum(axis=2))
self.labels = np.argmin(distances, axis=0)
# 更新质心
for j in range(self.k):
self.centroids[j] = X[self.labels == j].mean(axis=0)
def predict(self, X):
distances = np.sqrt(((X - self.centroids[:, np.newaxis])**2).sum(axis=2))
return np.argmin(distances, axis=0)
# generate sample data
X = np.random.randn(100, 2)
# initialize KMeans object and fit the data
kmeans = KMeans(k=3)
kmeans.fit(X)
# plot the results
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels)
plt.scatter(kmeans.centroids[:, 0], kmeans.centroids[:, 1], marker='x', color='r')
plt.show()
sklearn实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
plt.rcParams["font.family"]="SimHei"
# 设置正常显示字符
plt.rcParams["axes.unicode_minus"]=False
plt.rcParams["font.size"]=12
np.random.seed(0)
#生成样本数据
dataMat = np.random.randint(70,100,size=(50,2))
print(dataMat.shape)
# 训练模型
km = KMeans(n_clusters=4,n_init="auto") # 初始化
km.fit(dataMat) # 拟合
km_pred = km.predict(dataMat) # 预测
centers = km.cluster_centers_ # 质心
print(km_pred.shape)
print(centers.shape)
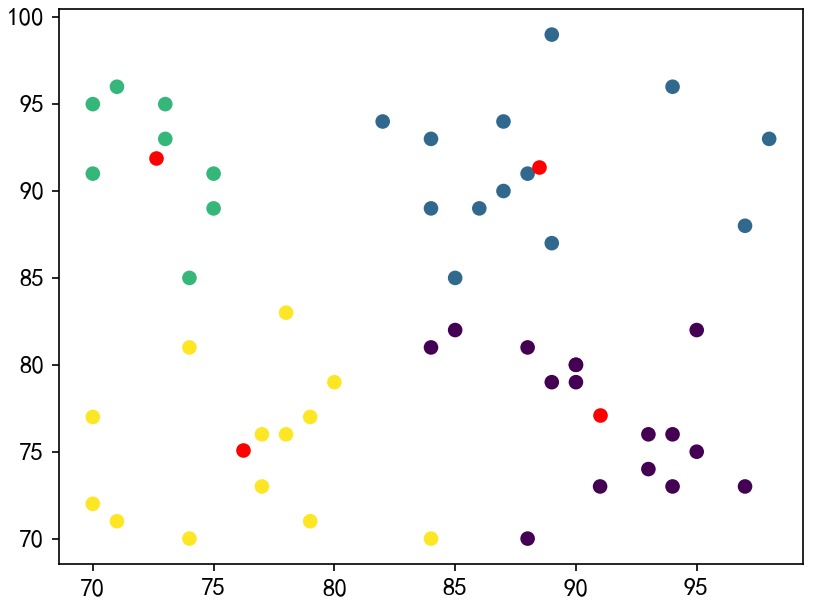
# 可视化结果
plt.scatter(np.array(dataMat)[:, 1], np.array(dataMat)[:, 0], c=km_pred)
plt.scatter(centers[:, 1], centers[:, 0], c="r")
plt.show()
# print() 结果
(50, 2)
(50, 2)
(4, 2)
参考资料
https://github.com/apachecn/ailearning/blob/master/docs/ml/10.md



