汽车加油行驶问题(分层图最短路)
时空限制1000ms / 256MB
题目描述
给定一个 N×N 的方形网格,设其左上角为起点◎,坐标(1,1),X 轴向右为正,Y 轴向下为正,每个方格边长为 1 ,如图所示。
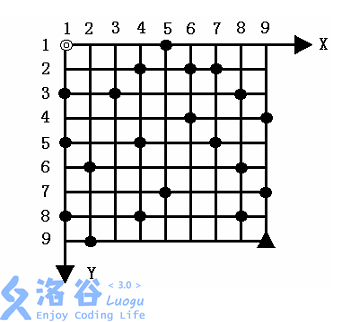
一辆汽车从起点◎出发驶向右下角终点▲,其坐标为 (N,N)。
在若干个网格交叉点处,设置了油库,可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:
-
汽车只能沿网格边行驶,装满油后能行驶 K 条网格边。出发时汽车已装满油,在起点与终点处不设油库。
-
汽车经过一条网格边时,若其 X 坐标或 Y 坐标减小,则应付费用 B ,否则免付费用。
-
汽车在行驶过程中遇油库则应加满油并付加油费用 A。
-
在需要时可在网格点处增设油库,并付增设油库费用 C(不含加油费用A )。
-
N,K,A,B,C 均为正整数, 且满足约束: 2≤N≤100,2≤K≤10。
设计一个算法,求出汽车从起点出发到达终点所付的最小费用。
输入输出格式
输入格式:文件的第一行是 N,K,A,B,C 的值。
第二行起是一个N×N 的 0−1 方阵,每行 N 个值,至 N+1 行结束。
方阵的第 i 行第 j 列处的值为 1 表示在网格交叉点 (i,j) 处设置了一个油库,为 0 时表示未设油库。各行相邻两个数以空格分隔。
输出格式:程序运行结束时,输出最小费用。
输入输出样例
说明
2≤n≤100,2≤k≤10
题目链接:https://www.luogu.org/problemnew/show/P4009
分层图最短路。这个汽车只能走k步的确是一个比较烦人的条件,但是k很小,所以可以考虑用分层图来约束这个k。即总共建k+1层图,只有层与层之间有边,汽车每走一步就会向上移动一层。建边规则满足题目要求即可。

#include<bits/stdc++.h> #define N 200005 using namespace std; int Map[105][105]; int num[105][105][15]; struct ss { int v,next,w; }; ss edg[N*4]; int head[N],now_edge=0; void addedge(int u,int v,int w) { edg[now_edge]=(ss){v,head[u],w}; head[u]=now_edge++; } int dis[N]; int vis[N]={0}; void spfa() { for(int i=0;i<N;i++)dis[i]=INT_MAX/2; dis[num[1][1][0]]=0; queue<int>q; q.push(num[1][1][0]); vis[num[1][1][0]]=1; while(!q.empty()) { int now=q.front(); q.pop(); vis[now]=0; for(int i=head[now];i!=-1;i=edg[i].next) { int v=edg[i].v; if(dis[v]>dis[now]+edg[i].w) { dis[v]=dis[now]+edg[i].w; if(!vis[v]) { q.push(v); vis[v]=1; } } } } } int main() { int n,k,a,b,c; memset(head,-1,sizeof(head)); scanf("%d %d %d %d %d",&n,&k,&a,&b,&c); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)scanf("%d",&Map[i][j]); int cnt=1; for(int kk=0;kk<=k;kk++) { for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) num[i][j][kk]=cnt++; } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { if(i+1<=n)addedge(num[i][j][0],num[i+1][j][1],0); if(j+1<=n)addedge(num[i][j][0],num[i][j+1][1],0); if(i-1>=1)addedge(num[i][j][0],num[i-1][j][1],b); if(j-1>=1)addedge(num[i][j][0],num[i][j-1][1],b); } for(int kk=1;kk<k;kk++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(!Map[i][j]) { if(i+1<=n)addedge(num[i][j][kk],num[i+1][j][kk+1],0); if(j+1<=n)addedge(num[i][j][kk],num[i][j+1][kk+1],0); if(i-1>=1)addedge(num[i][j][kk],num[i-1][j][kk+1],b); if(j-1>=1)addedge(num[i][j][kk],num[i][j-1][kk+1],b); addedge(num[i][j][kk],num[i][j][0],c+a); } else { addedge(num[i][j][kk],num[i][j][0],a); } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(!Map[i][j]) { addedge(num[i][j][k],num[i][j][0],c+a); } else { addedge(num[i][j][k],num[i][j][0],a); } spfa(); int ans=INT_MAX; for(int i=0;i<=k;i++)ans=min(ans,dis[num[n][n][i]]); printf("%d\n",ans); return 0; }
路漫漫其修远兮,吾将上下而求索


