校园网(有向图加边变成强连通图)

校园网Network of Schools

时空限制1000ms / 128MB

题目描述

一些学校连入一个电脑网络。那些学校已订立了协议：每个学校都会给其它的一些学校分发软件（称作“接受学校”）。注意即使 B 在 A 学校的分发列表中， A 也不一定在 B 学校的列表中。

你要写一个程序计算，根据协议，为了让网络中所有的学校都用上新软件，必须接受新软件副本的最少学校数目（子任务 A）。更进一步，我们想要确定通过给任意一个学校发送新软件，这个软件就会分发到网络中的所有学校。为了完成这个任务，我们可能必须扩展接收学校列表，使其加入新成员。计算最少需要增加几个扩展，使得不论我们给哪个学校发送新软件，它都会到达其余所有的学校（子任务 B）。一个扩展就是在一个学校的接收学校列表中引入一个新成员。

输入输出格式

输入格式：

输入文件的第一行包括一个整数 N：网络中的学校数目（2 <= N <= 100）。学校用前 N 个正整数标识。

接下来 N 行中每行都表示一个接收学校列表（分发列表）。第 i+1 行包括学校 i 的接收学校的标识符。每个列表用 0 结束。空列表只用一个 0 表示。

输出格式：

你的程序应该在输出文件中输出两行。

第一行应该包括一个正整数：子任务 A 的解。

第二行应该包括子任务 B 的解。

输入输出样例

输入样例： 

5
2 4 3 0
4 5 0
0
0
1 0

输出样例： 

1
2

说明

题目翻译来自NOCOW。

USACO Training Section 5.3

---

题意：1,选取最少的点，使得从这些点出发可以到达图中所有的点。2,添加最少边使图变成强连通图。

分析：因为一个强连通分量中的点可以相互到达，所以我们可以先缩点，这样给定的图就变成了一个DAG，对于第一问，只要选取了所有入度为零的点，从这些点出发就可以到达所有点。对于第二问，设sum1为有多少个点入度为零，设sum2为有多少个点出度为零，则答案为max（sum1,sum2）。加边方法为：先用min（sum1,sum2）条边连接入度为零和出度为零的点，若只有一个DAG则类似连成自环，若有多个DAG则类似连成一个大环，然后剩下的max(sum1,sum2)-min(sum1,sum2)条边随便连到环上就行了。

 

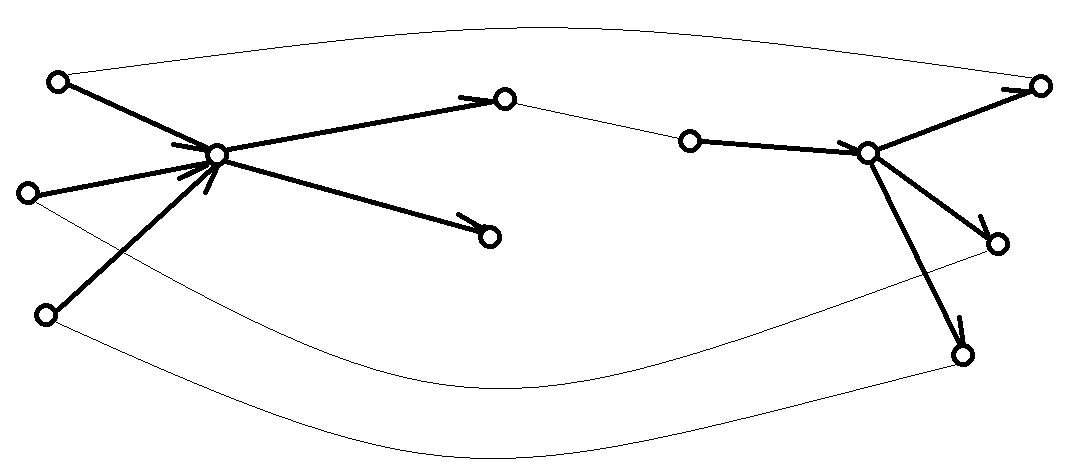
图例：两个DAG连成大环。

#include<bits/stdc++.h>
#define N 100050
using namespace std;

struct ss
{
    int to,next;
};

ss edg[N];
int head[N];
int now_edge=0;

void addedge(int u,int v)
{
    edg[now_edge]=(ss){v,head[u]};
    head[u]=now_edge++;
}


int dfn[N],low[N],color[N],now_clock,now_color;
int Stack[N],top;

void tarjan(int x)
{
    dfn[x]=low[x]=++now_clock;
    Stack[top++]=x;
    
    for(int i=head[x];i!=-1;i=edg[i].next)
    {
        int v=edg[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[x]=min(low[x],low[v]);
        }
        else
        if(!color[v])low[x]=min(low[x],dfn[v]);
    }
    
    if(low[x]==dfn[x])
    {
        now_color++;
        while(Stack[top-1]!=x)
        {
            color[Stack[--top]]=now_color;
        }
        color[Stack[--top]]=now_color;
    }
}

int ans[N];
int max_point[N]={0};

int dfs(int x)
{
    if(ans[x])return ans[x];
    int Max=max_point[x];
    for(int i=head[x];i!=-1;i=edg[i].next)
    Max=max(Max,dfs(edg[i].to));
    
    return ans[x]=Max;
}

void init()
{
    memset(ans,0,sizeof(ans));
    memset(head,-1,sizeof(head));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(color,0,sizeof(color));
    now_edge=0;
    top=1;
    now_color=0;
    now_clock=1;
}

vector<int>to_edge[N];

int main()
{
    int n;
    scanf("%d",&n);
    init();
    for(int i=1;i<=n;i++)
    {
        int a;
        scanf("%d",&a);
        while(a)
        {
            to_edge[i].push_back(a);
            addedge(i,a);
            scanf("%d",&a);
        }
    }

    for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
    
    int sum1=0,sum2=0;
    int rd[N]={0},cd[N]={0};
    
    for(int i=1;i<=n;i++)
    for(int j=0;j<to_edge[i].size();j++)
    {
        int u=color[i],v=color[to_edge[i][j]];
        if(u==v)continue;
        cd[u]++;
        rd[v]++;
    }
    
    for(int i=1;i<=now_color;i++)
    {
        if(rd[i]==0)sum1++;
        if(cd[i]==0)sum2++;
    }

    if(now_color==1){printf("1\n0\n");return 0;}

    printf("%d\n%d\n",sum1,max(sum1,sum2));
    return 0;
}