CSGO
CSGO
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Problem Description
You are playing CSGO.
There are n Main Weapons and m Secondary Weapons in CSGO. You can only choose one Main Weapon and one Secondary Weapon. For each weapon, it has a composite score S.
The higher the composite score of the weapon is, the better for you.
Also each weapon has K performance evaluations x[1], x[2], …, x[K].(range, firing rate, recoil, weight…)
So you shold consider the cooperation of your weapons, you want two weapons that have big difference in each performance, for example, AWP + CZ75 is a good choose, and so do AK47 + Desert Eagle.
All in all, you will evaluate your weapons by this formula.(MW for Main Weapon and SW for Secondary Weapon)
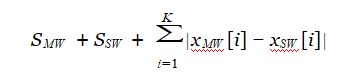
Now you have to choose your best Main Weapon & Secondary Weapon and output the maximum evaluation.
There are n Main Weapons and m Secondary Weapons in CSGO. You can only choose one Main Weapon and one Secondary Weapon. For each weapon, it has a composite score S.
The higher the composite score of the weapon is, the better for you.
Also each weapon has K performance evaluations x[1], x[2], …, x[K].(range, firing rate, recoil, weight…)
So you shold consider the cooperation of your weapons, you want two weapons that have big difference in each performance, for example, AWP + CZ75 is a good choose, and so do AK47 + Desert Eagle.
All in all, you will evaluate your weapons by this formula.(MW for Main Weapon and SW for Secondary Weapon)
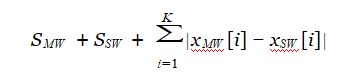
Now you have to choose your best Main Weapon & Secondary Weapon and output the maximum evaluation.
Input
Multiple query.
On the first line, there is a positive integer T, which describe the number of data. Next there are T groups of data.
for each group, the first line have three positive integers n, m, K.
then, the next n line will describe n Main Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
then, the next m line will describe m Secondary Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
There is a blank line before each groups of data.
T<=100, n<=100000, m<=100000, K<=5, 0<=S<=1e9, |x[i]|<=1e9, sum of (n+m)<=300000
On the first line, there is a positive integer T, which describe the number of data. Next there are T groups of data.
for each group, the first line have three positive integers n, m, K.
then, the next n line will describe n Main Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
then, the next m line will describe m Secondary Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
There is a blank line before each groups of data.
T<=100, n<=100000, m<=100000, K<=5, 0<=S<=1e9, |x[i]|<=1e9, sum of (n+m)<=300000
Output
Your output should include T lines, for each line, output the maximum evaluation for the corresponding datum.
Sample Input
2
2 2 1
0 233
0 666
0 123
0 456
2 2 1
100 0 1000 100 1000 100
100 0
Sample Output
543
2000
题意:求上面那个表达式的最大值。
这个表达式的后面很像曼哈顿距离,所以可以转换为求最远曼哈顿距离。
如何处理前面那两个正数:在每个点上再加一维,主武器权值为正,副武器权值为负。
如何让程序选的两个点分别在主武器集合和副武器集合里:更改主武器的某一维的权值,让其加上一个INF,这样选的最远曼哈顿距离肯定不会是同一个集合里的了,最后答案减去INF。

#include <stdio.h> #define INF 100000000000 #define M 200005//坐标个数 int D = 6;//空间维数 struct Point { long long x[6]; }pt[M]; long long dis[1<<6][M],minx[1<<6],maxx[1<<6];//去掉绝对值后有2^D种可能 void Get(int N)//取得所有点在指定状态(S)下的“本点有效距离” { int tot=(1<<D); for(int s=0;s<tot;s++)//遍历所有维数正负状态 { int coe[D]; for(int i=0;i<D;i++)//设定当前状态的具体正负参数 if(s&(1<<i)) coe[i]=-1.0; else coe[i]=1.0; for(int i=0;i<N;i++)//遍历所有点,确定每个点在当前状态下的“本点有效距离” { dis[s][i]=0; for(int j=0;j<D;j++) dis[s][i]=dis[s][i]+coe[j]*pt[i].x[j]; } } } //取每种可能中的最大差距 void Solve(int N) { int tot=(1<<D); long long tmp,ans; for(int s=0;s<tot;s++) { minx[s]=INF; maxx[s]=-INF; for(int i=0;i<N;i++) { if (minx[s]>dis[s][i]) minx[s]=dis[s][i]; if (maxx[s]<dis[s][i]) maxx[s]=dis[s][i]; } } ans=0; for(int s=0;s<tot;s++) { tmp=maxx[s]-minx[s]; if(tmp>ans) ans=tmp; } printf("%lld\n", ans-INF); } int main() { int t; scanf("%d",&t); while(t--) { int n,m,k; scanf("%d %d %d",&n,&m,&k); D=k+1; for(int i=0;i<n;i++) { for(int j=0;j<=k;j++) { scanf("%lld",&pt[i].x[j]); } pt[i].x[0]+=INF; } for(int i=0;i<m;i++) { for(int j=0;j<=k;j++) { scanf("%lld",&pt[i+n].x[j]); } pt[i+n].x[0]=-pt[i+n].x[0]; } Get(n+m); Solve(n+m); } return 0; }
路漫漫其修远兮,吾将上下而求索


