Sandglass

问题 I: Sandglass

时间限制: 1 Sec  内存限制: 128 MB

题目描述

We have a sandglass consisting of two bulbs, bulb A and bulb B. These bulbs contain some amount of sand. When we put the sandglass, either bulb A or B lies on top of the other and becomes the upper bulb. The other bulb becomes the lower bulb.
The sand drops from the upper bulb to the lower bulb at a rate of 1 gram per second. When the upper bulb no longer contains any sand, nothing happens.
Initially at time 0, bulb A is the upper bulb and contains a grams of sand; bulb B contains X−a grams of sand (for a total of X grams).
We will turn over the sandglass at time r1,r2,..,rK. Assume that this is an instantaneous action and takes no time. Here, time t refer to the time t seconds after time 0.
You are given Q queries. Each query is in the form of (ti,ai). For each query, assume that a=ai and find the amount of sand that would be contained in bulb A at time ti.

Constraints
1≤X≤10⁹
1≤K≤10⁵
1≤r1<r2<..<rK≤10⁹
1≤Q≤10⁵
0≤t1<t2<..<tQ≤10⁹
0≤ai≤X(1≤i≤Q)
All input values are integers.

 

样例输入

180
3
60 120 180
3
30 90
61 1
180 180

 

样例输出

60
1
120

---

题目大意是给你一个数，每次可以对这个数加一个数或者减去一个数，直到它要求的时间为止。且这个数最大为x最小为0.
考虑维护初始数为0和x这两个特殊的数，则到某一时间，任何初始状态的数都会在维护的这两个数之间，有如下关系图：

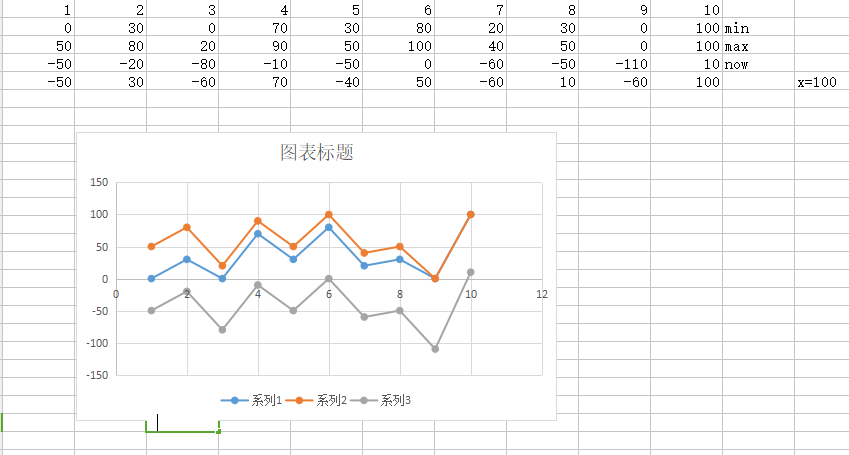
再计算一个不经过维护的数now，now的初始值也是0，这样将now加上初始的数，如果此时now还在min到max区间内，那么这个now就是答案，否则答案就是min或者max。
这是因为，如果初始值按照正常的顺序进行加减运算且进行维护，那么它的曲线一定是在min曲线和max曲线之间，一旦它和某一条曲线在某一点重合，那么以后这条曲线就都可以用重合的曲线代替了，换言之，
就是初始值经过运算且维护后，和最大值（或最小值）运算且维护后的答案相同。

#include <bits/stdc++.h>
#define N 100050
using namespace std;
pair<int,int>team[N];
 
int main()
{
   int x;
   int k;
   int t[N]={0};
   scanf("%d %d",&x,&k);
   for(int i=1;i<=k;i++)scanf("%d",&t[i]);
   int q;
   scanf("%d",&q);
   for(int i=0;i<q;i++)scanf("%d %d",&team[i].first,&team[i].second);
 
   long long MIN=0,MAX=x,NOW=0,ki=1,sign=-1;
   for(int i=0;i<q;i++)
   {
       while(ki<=k&&t[ki]<=team[i].first)
       {
           long long now=t[ki]-t[ki-1];
           now*=sign;
           sign*=-1;
 
           MIN+=now;
           MIN=max(MIN,(long long)0);
           MIN=min(MIN,(long long)x);
           MAX+=now;
           MAX=max(MAX,(long long)0);
           MAX=min(MAX,(long long)x);
 
           NOW+=now;
           ki++;
 
       }
 
       long long now=team[i].first-t[ki-1];
       now*=sign;
 
       long long ans=team[i].second+NOW;
       if(ans<MIN)ans=MIN;
       if(ans>MAX)ans=MAX;
 
       ans+=now;
 
        ans=max(ans,(long long)0);
        ans=min(ans,(long long)x);
       printf("%d\n",ans);
   }
 
    return 0;
}