JavaScript WebGL 三维相关概念
目录
引子
在 JavaScript WebGL 矩阵之后,发现在实现三维效果之前还有一些概念需要理解,就去查了下资料,按照自己的习惯整合了一下。
齐次坐标
三维坐标理论上三个分量就够了,但在看相关程序的时候,发现会出现 4 个分量,这种表示方式称为齐次坐标,它将一个原本 n 维向量用一个 n+1 维向量表示。比如向量 (x, y, z) 的齐次坐标可表示为 (x, y, z, w)。这样表示有利于使用矩阵运算将一个点集从一个坐标系转换到另一个坐标系。齐次坐标 (x, y, z, w) 等价于三维坐标 (x/w, y/w, z/w) 。更详细介绍见这里。
空间转换
WeGL 没有现成 API 可以直接绘制出三维效果,需要进行一系列空间转换,最终在二维空间(比如电脑屏幕)显示,从视觉上看上去是三维立体效果。下面看看几个主要转换过程。
模型空间
模型空间是描述三维物体自身的空间,拥有自己的坐标系和对应原点。这里点坐标可以按照 WebGL 中可见范围 [-1, +1] 约束进行描述,也可以不按照这个约束。自定义描述规则后面需要转换一下。
世界空间
物体模型创建好后,放在具体环境当中,才会达到想要的效果,除此之外,还可能会进行位移、缩放和旋转,进行这些变化都需要一个新参考坐标系,这个所处环境就是世界空间。有了世界坐标系,相互独立的物体才会有相对位置的描述。
从模型空间转换到世界空间,需要用到模型矩阵(Model Matrix)。
三维模型矩阵跟 JavaScript WebGL 矩阵中介绍的二维变换矩阵类似,主要变化是行列增加和旋转。
点击展开代码
const m4 = {
translation: (x, y, z) => {
return [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
x, y, z, 1,
];
},
// 缩放矩阵
scaling: (x, y, z) => {
return [
x, 0, 0, 0,
0, y, 0, 0,
0, 0, z, 0,
0, 0, 0, 1,
];
},
// 旋转矩阵
xRotation: (angle) => {
const c = Math.cos(angle);
const s = Math.sin(angle);
return [
1, 0, 0, 0,
0, c, s, 0,
0, -s, c, 0,
0, 0, 0, 1,
];
},
yRotation: (angle) => {
const c = Math.cos(angle);
const s = Math.sin(angle);
return [
c, 0, s, 0,
0, 1, 0, 0,
-s, 0, c, 0,
0, 0, 0, 1,
];
},
zRotation: (angle) => {
const c = Math.cos(angle);
const s = Math.sin(angle);
return [
c, s, 0, 0,
-s, c, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1,
];
},
}
视图空间
人眼在观察一个立方体时,从远处看和从近处看会有大小的差别,从左边看和从右边看会看到不同的面,在 WebGL 中绘制三维物体时,需要根据观察者的位置和方向,将物体放到正确的位置,观察者所处的空间就是视图空间。
从世界空间转换到视图空间,需要用到视图矩阵(View Matrix)。
为了描述观察者的状态,需要下面一些信息:
- 视点:观察者所在空间的位置,从这个位置沿着观察方向的射线为视线。
- 观察目标点:被观察目标所在的点,视点和观察目标点共同决定了视线的方向。
- 上方向:最终绘制在屏幕上影像向上的方向,因为观察者是可以围绕视线进行旋转,所以需要一个具体的参考方向。
上面的三种信息共同构成视图矩阵,WebGL 中观察者的默认状态为:
- 视点:位于坐标系统原点 (0, 0, 0)
- 观察目标点:视线是 z 轴负方向,观察点为 (0, 0, -1)
- 上方向:y 轴正方向,(0, 1, 0)
生成视图矩阵一种方法:
function setLookAt(eye, target, up) {
const [eyeX, eyeY, eyeZ] = eye;
const [targetX, targetY, targetZ] = target;
const [upX, upY, upZ] = up;
let fx, fy, fz, sx, sy, sz, ux, uy, uz;
fx = targetX - eyeX;
fy = targetY - eyeY;
fz = targetZ - eyeZ;
// 单位化
const rlf = 1 / Math.sqrt(fx * fx + fy * fy + fz * fz);
fx *= rlf;
fy *= rlf;
fz *= rlf;
// f 与上向量的叉乘
sx = fy * upZ - fz * upY;
sy = fz * upX - fx * upZ;
sz = fx * upY - fy * upX;
// 单位化
const rls = 1 / Math.sqrt(sx * sx + sy * sy + sz * sz);
sx *= rls;
sy *= rls;
sz *= rls;
// s 和 f 的叉乘
ux = sy * fz - sz * fy;
uy = sz * fx - sx * fz;
uz = sx * fy - sy * fx;
const m12 = sx * -eyeX + sy * -eyeY + sz * -eyeZ;
const m13 = ux * -eyeX + uy * -eyeY + uz * -eyeZ;
const m14 = -fx * -eyeX + -fy * -eyeY + -fz * -eyeZ;
return [
sx, ux, -fx, 0,
sy, uy, -fy, 0,
sz, uz, -fz, 0,
m12,m13, m14, 1,
];
}
这里用到了叉乘,通过两个向量的叉乘,可以生成垂直于这两个向量的法向量,从而构建一个坐标系,也就是观察者所在的空间。
下面是三维有无自定义观察者的示例:
裁剪空间
基于上面的示例,旋转一下就会发现有部分角消失的现象,这是因为超出了 WebGL 的可视范围。
在 WebGL 程序中,顶点着色器会将点转换到一个称为裁剪空间的特殊坐标系上。延展到裁剪空间之外的任何数据都会被剪裁并且不会被渲染。
从视图空间转换到裁剪空间,需要用到投影矩阵(Projection Matrix)。
可视域
人眼的观察范围是有限的,WebGL 类似的限制了水平视角、垂直视角和可视深度,这些共同决定了可视域(View Volume)。
有两类常见的可视域:
- 长方体/盒状可视域,由正射投影产生。
- 四棱锥/金字塔可视域,由透视投影产生。
正射投影可以方便的比较场景中物体的大小,因为物体看上去的大小与所在位置没有关系,在建筑平面等技术绘图相关场合,应当使用这种投影。透视投影让产生的场景看上去更有深度,更加自然。
正射投影
正射投影的可视域由前后两个矩形表面确定,分别称为近裁剪面和远裁剪面,近裁剪面和远裁剪面之间的空间就是可视域,只有在这个空间内的物体会被显示出来。正射投影下,近裁剪面和远裁剪面的尺寸是一样的。
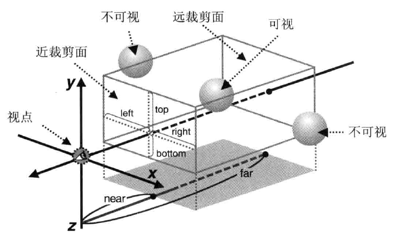
正射投影矩阵实现的一种方式:
function setOrthographicProjection(config) {
const [left, right, bottom, top, near, far] = config;
if (left === right || bottom === top || near === far) {
throw "Invalid Projection";
}
const rw = 1 / (right - left);
const rh = 1 / (top - bottom);
const rd = 1 / (far - near);
const m0 = 2 * rw;
const m5 = 2 * rh;
const m10 = -2 * rd;
const m12 = -(right + left) * rw;
const m13 = -(top + bottom) * rh;
const m14 = -(far + near) * rd;
return [
m0, 0, 0, 0,
0, m5, 0, 0,
0, 0, m10, 0,
m12, m13, m14, 1,
];
}
这是示例,通过改变各个边界感受可视范围变化。更加详细的原理解释见这里。
Canvas 上显示的就是物体在近裁剪面上的投影。如果裁剪面的宽高比和 Canvas 的不一样,画面就会按照 Canvas 的宽高比进行压缩,物体会被扭曲。
透视投影
透视投影的可视域产生跟正射投影的类似,比较明显的区别就是近裁剪面和远裁剪面尺寸不一样。
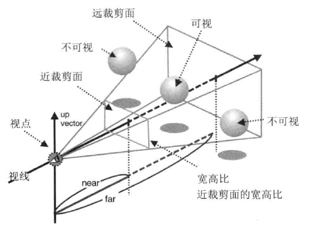
透视投影矩阵实现的一种方式:
/**
* 透视投影
* @param {*} config 顺序 fovy, aspect, near, far
* fovy - 垂直视角,可是空间顶面和底面的夹角,必须大于 0
* aspect - 近裁剪面的宽高比(宽/高)
* near - 近裁剪面的位置,必须大于 0
* far - 远裁剪面的位置,必须大于 0
*/
function setPerspectiveProjection(config) {
let [fovy, aspect, near, far] = config;
if (near === far || aspect === 0) {
throw "null frustum";
}
if (near <= 0) {
throw "near <= 0";
}
if (far <= 0) {
throw "far <= 0";
}
fovy = (Math.PI * fovy) / 180 / 2;
const s = Math.sin(fovy);
if (s === 0) {
throw "null frustum";
}
const rd = 1 / (far - near);
const ct = Math.cos(fovy) / s;
const m0 = ct / aspect;
const m5 = ct;
const m10 = -(far + near) * rd;
const m14 = -2 * near * far * rd;
return [
m0, 0, 0, 0,
0, m5, 0, 0,
0, 0, m10,-1,
0, 0, m14, 0,
];
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号