碰撞检测 :Separating Axis Theorem
目录
引子
在 Collision Detection :Transformation 中介绍了动态的碰撞检测,至此 CollisionDetection 项目的主要内容差不多都涉及了。在查询资料的时候,还接触到一些其它的检测方法,现在来看一下另外一种检测方法: Separating Axis Theorem 。
相关知识点
矢量和标量
简单的来说:
- 矢量(vector)也称向量,有大小和方向的量,例如加速度、力。
- 标量(scalar)只有大小(magnitude)的量,例如时间、温度。
在几何中,矢量用有向线段表示,表示如下:
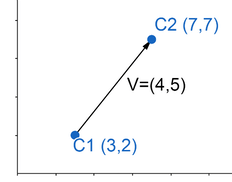
矢量 V 计算方法:
- V = C2 - C1
- V = (7-3,7-2)
- V = (4,5)
法向量:向量的垂直向量,交换 x 和 y 分量,然后将坐标 x 分量取反。上面 V 的法向量为 (-5,4) 。
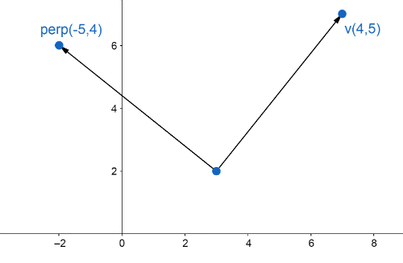
点积和投影
点积
两个矢量,可以用点积(Dot Product)的方式进行相乘,结果是一个标量。表示形式为: A · B 。
点积有两种计算方式:
方式一
A · B = Ax * Bx + Ay * By
方式二
A · B = |A| * |B| * cos(θ)
- |A| 是矢量 A 的量值
- |B| 是矢量 A 的量值
- θ 是矢量 A 和 B 之间的角度
还需要了解的一个概念就是单位向量,单位向量计算方法:向量除以向量自身的量值。
A / |A|
更多信息见这里。
投影
关于投影(Projection),先看下图:
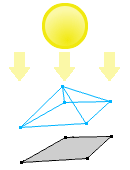
想象用一个发出平行光线的光源,照射到一个物体上,将在一个面上产生阴影。这个阴影是三维物体的二维投影。
类似的,二维物体的投影就是一维的“阴影”。
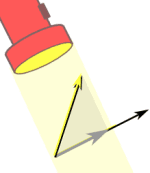
点积和投影的关系
利用点积可以得出一个矢量在另外一个矢量上的投影。通过简单的推导就可以明白。
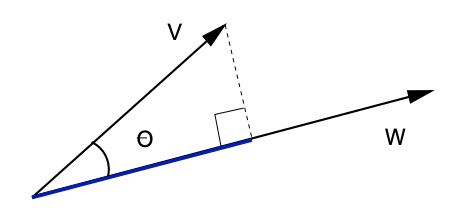
如上图所示,将 V 在 W 上的投影标量记为 Pw(V),可以得知:
Pw(V) = |V| * cos(θ)
根据点积计算方法得知:
V · W = |V| * |W| * cos(θ)
V * (W / |W|) = |V| * cos(θ)
因此可以得出:
Pw(V) = |V| * cos(θ) = V * (W / |W|)
多边形
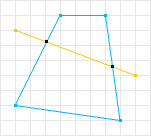
凸多边形
一条直线穿过一个多边形时,如果该线与多边形相交不超过(包含)两次,则该多边形为凸多边形(Convex Polygon)。
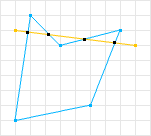
凹多边形
一条直线穿过一个多边形时,如果该线与多边形相交超过两次,则该多边形为凹多边形(Concave Polygon)。
Separating Axis Theorem
分轴理论(Separating Axis Theorem)由 Hermann Minkowski 提出,可用于解决凸多边形碰撞问题,该理论表明:
如果存在一条轴线,两个凸面物体在该轴上的投影没有重叠,那么这两个凸面物体就没有重叠。
这个轴线称为分轴。接下来进一步讨论一下。在下文中分轴理论简称 SAT 。
没有重叠
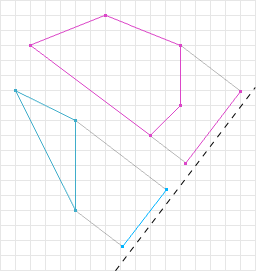
在上图中,可以看到投影没有重叠,根据 SAT ,这个两个形状没有重叠。
SAT 在检测的时候,可能需要检测很多轴线,但只要检测到有一个轴线上投影没有重叠,就可以停止继续检测。由于这种特点,SAT 对于有很多物体但碰撞很少的应用(游戏、模拟等等)是理想的选择。
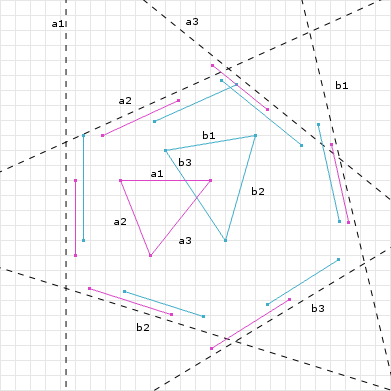
重叠
如果在所有分轴上,形状的投影都重叠,那么我们可以确定这些形状产生了重叠。示例如下:
算法实现
有了上面的原理,接下来转换成算法需要考虑的问题有:
- 如何获取到所有潜在的分轴?
- 投影重叠判断依据是什么?
问题 1
通过查找资料,第一个问题的答案是:在 2D 中,所有潜在的分轴是形状每条边的法线。
法线简单来说就是没有方向的法向量。在前面的知识点中有介绍。下面是一个大概逻辑实现:
const vertices = [] // 顶点的坐标集合,假设已有值
const axes = [] // 存放分轴
const verticesLen = vertices.length;
for (let i = 0; i < verticesLen; i++) {
const p1 = vertices[i];
const p2 = vertices[i + 1 == vertices.length ? 0 : i + 1];
// 获取每条边的矢量代数表示,subtract 方法功能主要功能是 p2 的坐标与 p1 坐标分量相减
const edge = subtract(p1,p2);
// 获取法向量,normalAxes 方法主要功能: (x, y) => (-y, x) or (y, -x)
const normal = normalAxes(edge);
axes.push(normal);
}
问题 2
在上面的关于 SAT 的介绍中,在图示中可以比较明显观察到,在算法实现中,需要遍历形状所有的顶点与分轴执行点积,比较获得最小值和最大值。然后在一条轴线上大概标注出最小值和最大值,看是否有重叠的区间。
下面是一个大概逻辑实现:
假设有多边形 A 和多边形 B 。
const verticesA = []; // A 形状所有顶点坐标集合
const verticesB = []; // B 形状所有顶点坐标集合
const axes = [] // 存储获取的所有分轴
const axesLen = axes.length;
for (let i = 0; i < axesLen; i++) {
const separateAxes = axes[i];
// getProject 方法获取投影的最大和最小值
const projectA = getProject(separateAxes,verticesA);
const aMin = projectA.min;
const aMax = projectA.max;
const projectB = getProject(separateAxes,verticesB);
const bMin = projectB.min;
const bMax = projectB.max;
// 符合该条件,表示投影重叠了。
if ( (aMin <= bMax && aMin >= bMin) || (bMin <= aMax && bMin >= aMin) ) {
continue;
} else {
return false;
}
}
验证
根据上面的思路,以网页左上角作为坐标原点,水平向左作为 X 轴,垂直向下作为 Y 轴。根据 CSS 的单位描述坐标点。
这个是测试页面,移动端如下:

在上面测试页面中,以未重叠的投影数据为例,检测的数据投影到一条轴线上:
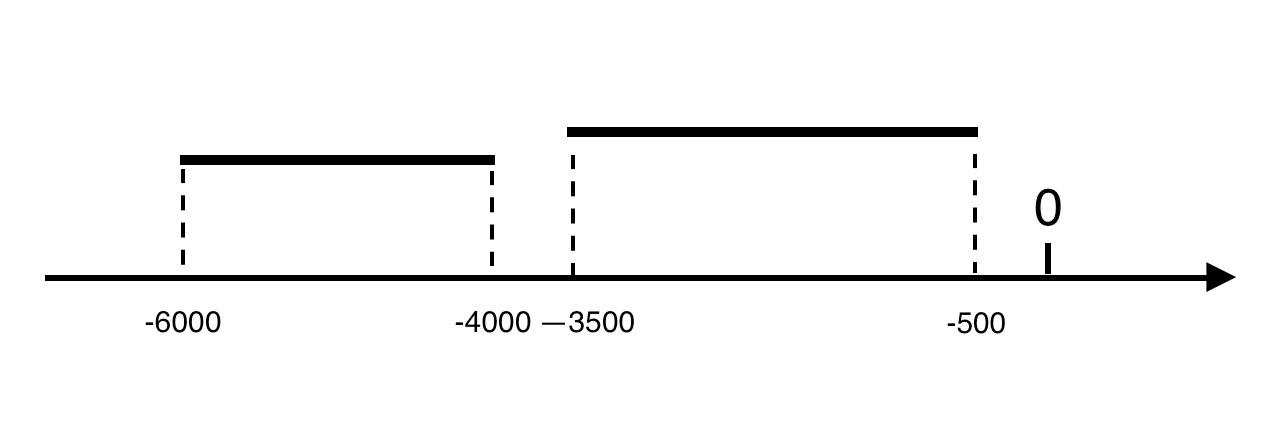
可以看出没有重叠。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号