碰撞检测 : Transformation
目录
引子
在 Collision Detection :Triangle 中对三角形的碰撞检测从另外一种思路进行思考,到目前为止介绍的都是静态的检测,接着来看一下动态的碰撞检测。
以下示例未做兼容性检查,建议在最新的 Chrome 浏览器中查看。
Transformation
这是示例页面。
基于 canvas 的 translate、 rotate、 scale 三种转换形成的动画,看看如何进行动态的碰撞检测。
基于 canvas 的动画原理是每隔一段时间进行重绘,所以在检测的时候,实际上是在特定的时刻,进行静态的碰撞检测,所以之前介绍的方法同样适用,这里统一使用 Polygon/Polygon 中的方法。 检测方法有了,接着就是获取在屏幕中相关点动态变化的坐标。下面分情况进行说明。
translate
在 canvas 上进行绘制时,都是基于坐标系进行定位,画布左上角为坐标系原点,水平向右为 X 轴正方向,垂直向下为 Y 轴正方向。绘制一个矩形 rect(20, 20, 40, 40) ,在坐标系上是这样的:
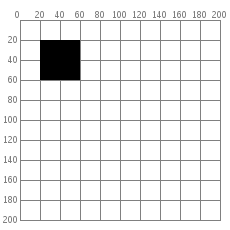
如果想要水平向右移动 60 像素,垂直向下移动 80 像素,可以直接进行坐标相加:rect(20 + 60, 20 + 80, 40, 40) 。
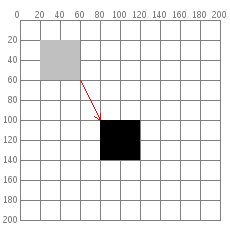
但还有另外一种更有趣的方式:移动整个坐标轴。如果把整个坐标轴水平向右移动 60 像素,垂直向下移动 80 像素,在视觉上是完全一样的。 translate 方法就是使用这种方式。
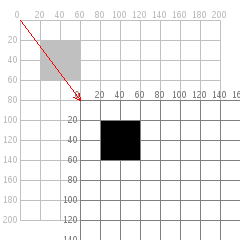
从上图可以发现,这种方式不用考虑矩形的坐标变化,在处理比较复杂的图形时,会方便很多。
需要注意的是,在进行了 translate 后,需要重置坐标轴,因为可能还有其它图形存在,而且还是以原来的坐标轴作为参考。重置坐标轴使用 setTransform 方法:
var canvas = document.getElementById("canvas");
var ctx = canvas.getContext("2d");
ctx.translate(50, 50);
ctx.fillRect(0,0,100,100);
// 重置
ctx.setTransform(1, 0, 0, 1, 0, 0);
// 其它处理
对于变化后的坐标,直接对平移的像素进行加减。
/**
* 假设点 A(x,y),经过 translate(x1,y1) 后达到 B(m,n)
*/
const m = x + x1;
const n = y + y1;
rotate
rotate 方法与 translate 方法类似,通过旋转坐标轴实现。

对于变化后的坐标,需要进行一些计算。
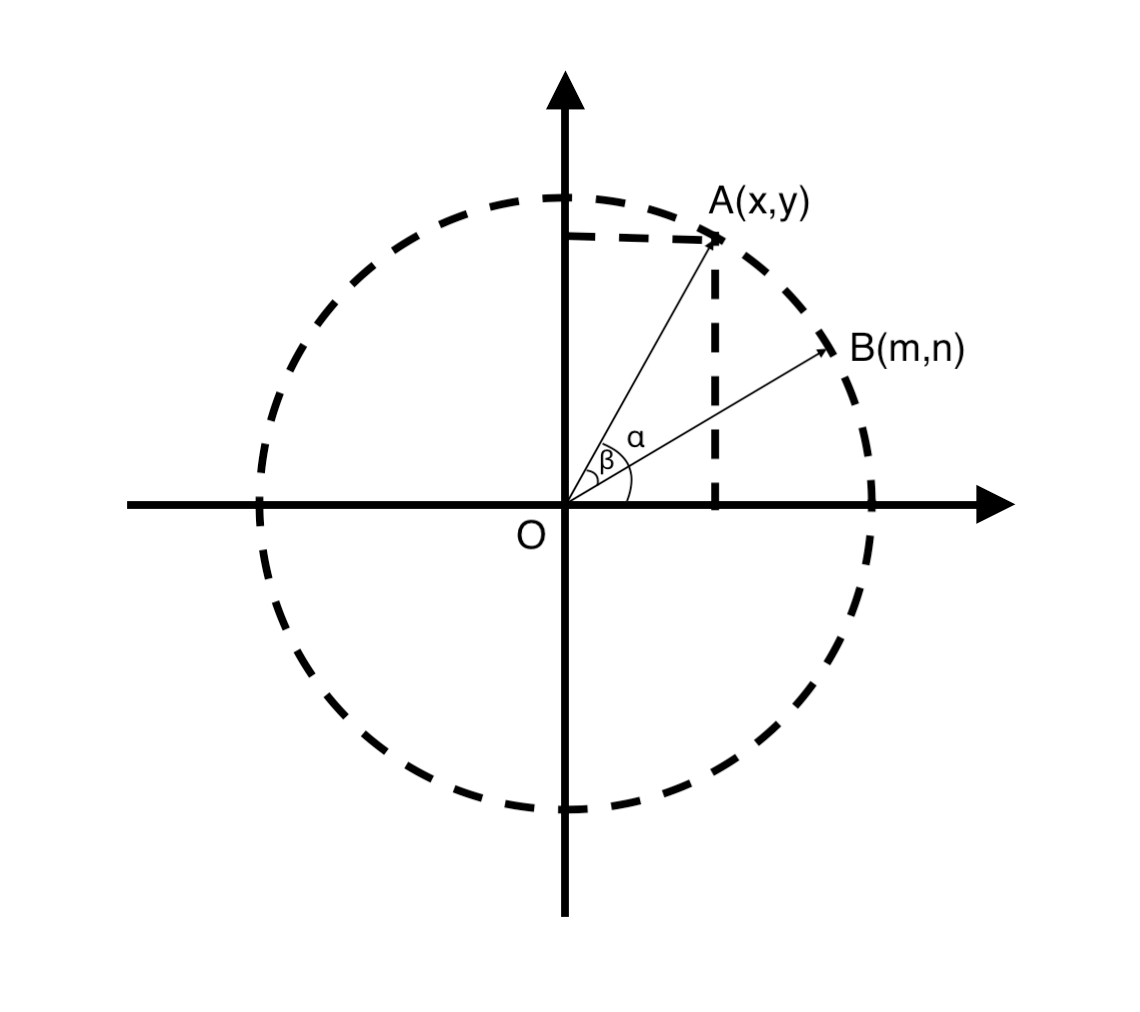
/**
*
* 圆心坐标 O(0,0),假设点 A(x,y) ,与 X 轴形成的角度为 α
* 顺时针旋转角度 β 后达到点 B(m,n),下面来推导一下 B 点坐标
*
* A 到圆心的距离: dist1 = |OA| = y/sin(α)=x/cos(α)
* B 到圆心的距离: dist2 = |OB| = n/sin(α-β)=m/cos(α-β)
*
* 只是旋转 所以 dist1 = dist2,建设旋转的半径为 r :
* r = y/sin(α)=x/cos(α)=n/sin(α-β)=m/cons(α-β)
* y = r * sin(α) x = r * cos(α)
*
* 根据三角函数公式:
* sin(α+β)=sin(α)cos(β)+cos(α)sin(β)
* sin(α-β)=sin(α)cos(β)-cos(α)sin(β)
* cos(α+β)=cos(α)cos(β)-sin(α)sin(β)
* cos(α-β)=cos(α)cos(β)+sin(α)sin(β)
*
* 代入下面公式:
* m = r*cos(α-β) = r * cos(α)cos(β) + r * sin(α)sin(β) = x * cos(β) + y * sin(β)
* n = r*sin(α-β) = r * sin(α)cos(β) - r * cos(α)sin(β) = y * cos(β) - x * sin(β)
*
* 逆时针则相反:
* m = x * cos(β) - y * sin(β)
* n = y * cos(β) + x * sin(β)
*
*/
scale
scale 方法 translate 方法类似,通过缩放坐标轴实现。
对于变化后的坐标,直接乘以对应缩放的倍数。
/**
* 假设点 A(x,y),经过 scale(num1,num2) 后达到 B(m,n)
*/
const m = x * num1;
const n = y * num2;
Transformation Order
当连续进行多次不同变换时,顺序不同,结果可能会不一样。这是示例。
这是因为连续进行变换时,都是基于上一次变换后的状态,再次进行变换。在进行计算的时候,需要多方面考虑。基于 transform 中的参数格式,进行计算会比较方便一些,translate、 rotate、 scale 的效果都可以转换为 transform 的形式。
/**
* canvas.transform(sx, ry, rx, sy, tx, ty)
* sx-水平缩放,ry-垂直倾斜,rx-水平倾斜,sy-垂直缩放,tx-水平移动,ty-垂直移动
*
*/
function Transform() {
this.reset();
}
Transform.prototype.reset = function() {
this.transformData = [1,0,0,1,0,0];
};
Transform.prototype.translate = function(x, y) {
let [sx,ry,rx,sy,tx,ty] = this.transformData;
const newTX = sx * x + rx * y;
const newTY = ry * x + sy * y;
this.transformData = [sx,ry,rx,sy,newTX,newTY];
};
Transform.prototype.rotate = function(angle) {
let c = Math.cos(angle);
let s = Math.sin(angle);
let [sx,ry,rx,sy,tx,ty] = this.transformData;
let newSX = sx * c + rx * s;
let newRY = ry * c + sy * s;
let newRX = sx * -s + rx * c;
let newSY = ry * -s + sy * c;
this.transformData = [newSX,newRY,newRX,newSY,tx,ty];
};
Transform.prototype.scale = function(x, y) {
let [sx,ry,rx,sy,tx,ty] = this.transformData;
let newSX = sx * x;
let newRY = ry * x;
let newRX = rx * y;
let newSY = sy * y;
this.transformData = [newSX,newRY,newRX,newSY,tx,ty];
};
Transform.prototype.getCoordinate = function(x, y) {
let [sx,ry,rx,sy,tx,ty] = this.transformData;
const px = x * sx + y*rx + tx;
const py = x * ry + y*sy + ty;
return [px,py];
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号