碰撞检测 ：Triangle
引子
在 Collision Detection ：Polygon 中主要介绍了多边形相关的碰撞检测，接着来看看三角形的情况。三角形同样属于多边形，因此，多边形的方法对三角形都适用。在这里探讨一下另外一种思路。
以下示例未做兼容性检查，建议在最新的 Chrome 浏览器中查看。
Triangle/Point
这是示例页面。
三角形与点的碰撞检测，可以从面积的角度进行切入，看下面的一张图：
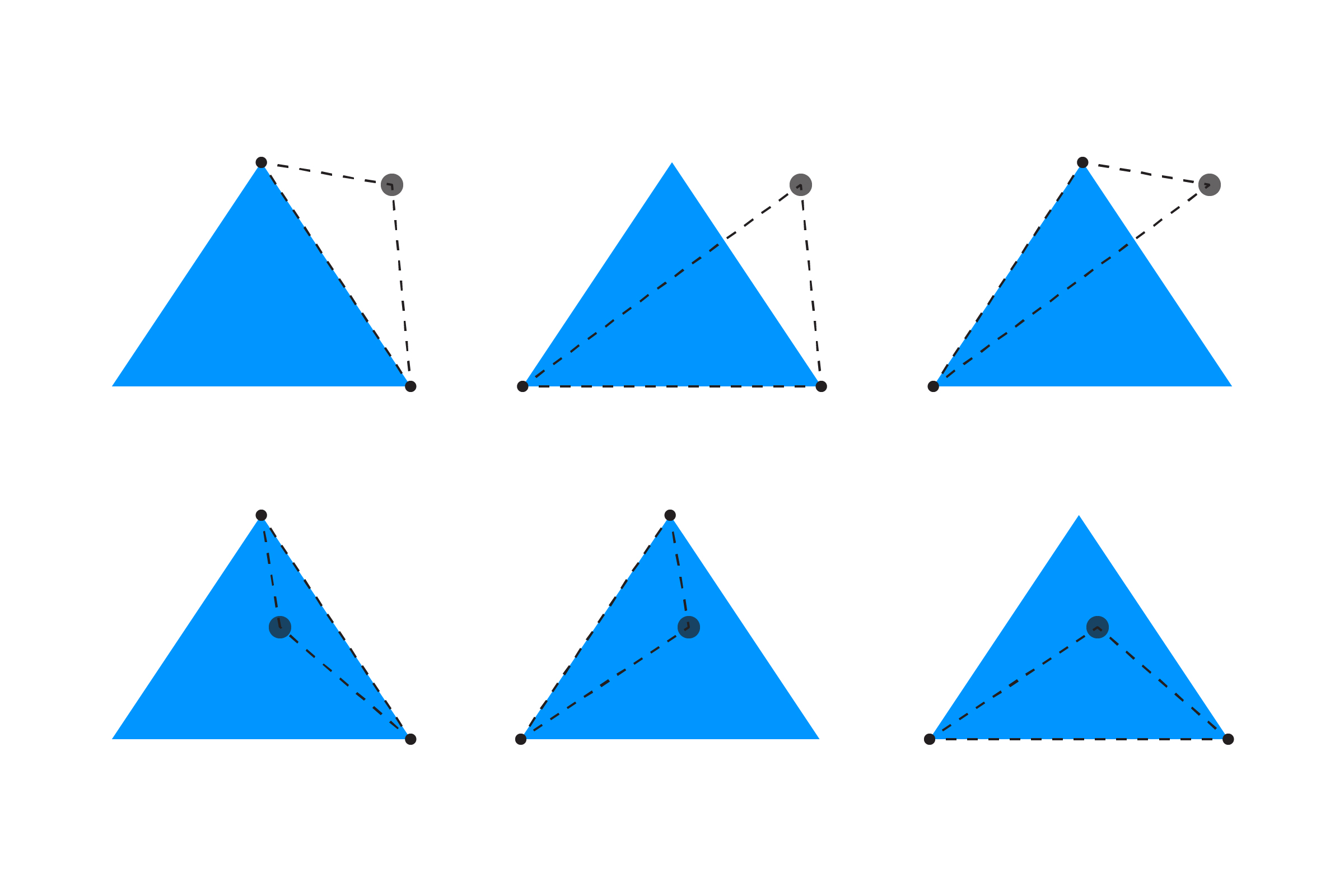
如果点在三角形内，那么与三角形顶点相连，切割成了三部分，这三部分的面积之和，如果跟三角形面积相等，那么就可以说明发生了碰撞。
/**
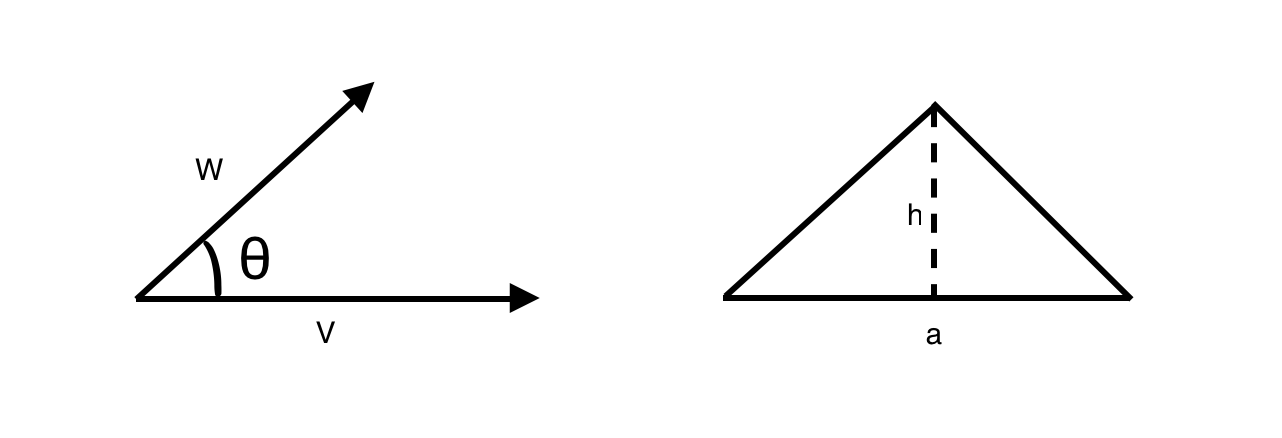
* 叉积 用符号 x 表示
* V 矢量
* W 矢量
* |V| |W| 矢量的模，就是线段实际长度
* θ V 与 W 之间的角度
*/
V x W = |V| * |W| * sin(θ)
/**
* 计算面积公式
* a 底
* h 高
*/
S = a * h * 1/2
从上图中可以看出 |W| * sin(θ) 的结果就是三角形的高 h ，也就是说：
S = a * h * 1/2 = V x W *1/2
基于上面的理论支持，下面是完整检测逻辑：
/*
* points 三角形顶点坐标，形式为 [[x1,y1],[x2,y2]]
* (px,py) 检测点坐标
*/
function checkTrianglePoint({points,px,py}) {
const [point1,point2,point3] = points;
const [x1,y1] = point1;
const [x2,y2] = point2;
const [x3,y3] = point3;
// 原始总面积
const areaOrig = Math.abs( (x2-x1)*(y3-y1) - (x3-x1)*(y2-y1) );
// 检测点与三角形顶点形成的面积
const area1 = Math.abs( (x1-px)*(y2-py) - (x2-px)*(y1-py) );
const area2 = Math.abs( (x2-px)*(y3-py) - (x3-px)*(y2-py) );
const area3 = Math.abs( (x3-px)*(y1-py) - (x1-px)*(y3-py) );
const areaTotal = area1 + area2 + area3;
// 计算误差允许值
const buffer = 0.1;
if (areaTotal >= areaOrig-buffer && areaTotal<= areaOrig+buffer) {
return true;
}
return false;
}
