线段树
原理
(注:由于线段树的每个节点代表一个区间,以下叙述中不区分节点和区间,只是根据语境需要,选择合适的词)
线段树本质上是维护下标为1,2,..,n的n个按顺序排列的数的信息
所以 其实是“点树” 是维护n的点的信息 至于每个点的数据的含义可以有很多
在对线段操作的线段树中 每个点代表一条线段 在用线段树维护数列信息的时候 每个点代表一个数 但本质上都是每个点代表一个数
以下 在讨论线段树的时候 区间[L,R]指的是下标从L到R的这(R-L+1)个数 而不是指一条连续的线段
只是有时候这些数代表实际上一条线段的统计结果而已
线段树是将每个区间[L,R]分解成[L,M]和[M+1,R] (其中M=(L+R)/2 这里的除法是整数除法,即对结果下取整)直到 L==R 为止
开始时是区间[1,n] 通过递归来逐步分解 假设根的高度为1的话 树的最大高度为![]() (n>1)
(n>1)
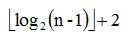 (n>1)
(n>1)线段树对于每个n的分解是唯一的 所以n相同的线段树结构相同
下图展示了区间[1,13]的分解过程:
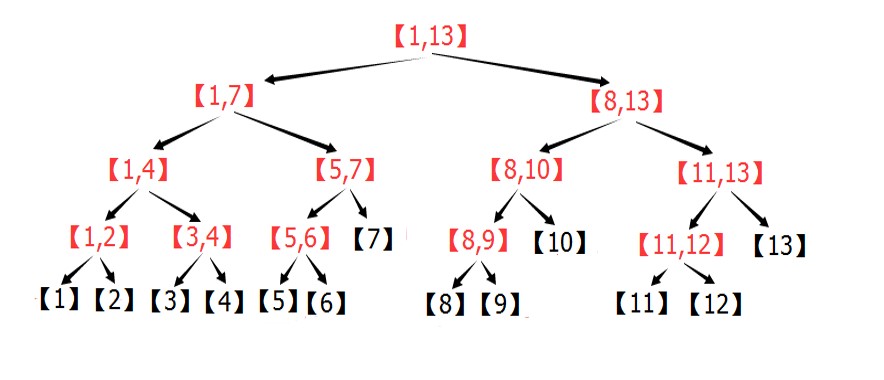
上图中 每个区间都是一个节点 每个节点存自己对应的区间的统计信息
代码
单点修改

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cmath> 5 #include<string> 6 #include<algorithm> 7 #include<map> 8 #include<queue> 9 #include<stack> 10 #include<set> 11 #include<vector> 12 using namespace std; 13 typedef long long ll; 14 const int maxn = 5e5 + 5; 15 int l[4 * maxn], r[4 * maxn]; 16 ll sum[4 * maxn]; 17 void build(int L, int R, int now)//输入的时候L是1,R是数列长度,now == 1 18 { 19 l[now] = L; r[now] = R; 20 if(L == R) 21 { 22 /* 递归边界:左右端点重合,说明此时区间里只有一个元 23 素,正好就可以读入数据,而且此时读入的也正好是该区间 24 的区间和 */ 25 scanf("%lld", &sum[now]); 26 return ; 27 } 28 int mid = (L + R) >> 1; 29 build(L, mid, now << 1); //构建左子树 30 build(mid + 1, R, now << 1 | 1);//构建右子树,注意从 mid + 1开始 31 sum[now] = sum[now << 1] + sum[now << 1 | 1]; 32 // 该区间和就等于左右子区间和的加和 33 } 34 35 void update(int idx, int d, int now){//idx为输入数列中的序号, d为增加值, now == 1 36 //idx 代表结点编号,d 代表这个数加上 d 37 sum[now] += d; 38 if (l[now] == r[now]) return; //到达叶结点了 39 int mid = (l[now] + r[now]) >> 1; 40 //然后判断要更新的点在左还是右子树中 41 if (idx <= mid) update(idx, d, now << 1); 42 else update(idx, d, now << 1 | 1); 43 } 44 45 46 ll query(int L, int R, int now){//L R表示区间[L, R], now == 1, 函数返回值为区间和 47 if (L == l[now] && R == r[now]) return sum[now]; 48 int mid = (l[now] + r[now]) >> 1; 49 if (R <= mid) return query(L, R, now << 1); 50 else if (L > mid) return query(L, R, now << 1 | 1); 51 else return query(L, mid, now << 1) + query(mid + 1, R, now << 1 | 1); 52 //没什么好解释的吧,很好理解 53 } 54 55 int main() 56 { 57 int n, q; scanf("%d%d", &n, &q); 58 build(1, n, 1); 59 while(q--) 60 { 61 int op, a, b; scanf("%d%d%d", &op, &a, &b); 62 if (op == 1) update(a, b - query(a, a, 1), 1); 63 else printf("%lld\n", query(a, b, 1)); 64 } 65 return 0; 66 }
区间修改
1.区间加值
1 //区间加值 2 #include<cstdio> 3 #include<iostream> 4 #include<cstring> 5 #include<cmath> 6 #include<string> 7 #include<algorithm> 8 #include<map> 9 #include<queue> 10 #include<stack> 11 #include<set> 12 #include<vector> 13 typedef long long ll; 14 using namespace std; 15 void pushup(int o) { 16 //pushup函数,该函数本身是将当前结点用左右子节点的信息更新,此处求区间和,用于update中将结点信息传递完返回后更新父节点 17 st[o] = st[o<<1] + st[o<<1|1]; 18 } 19 20 void pushdown(int o,int l,int r) { 21 //pushdown函数,将o结点的信息传递到左右子节点上 22 if(add[o]) { 23 //当父节点有更新信息时才向下传递信息 24 add[o<<1] += add[o]; 25 //左右儿子结点均加上父节点的更新值 26 add[o<<1|1]+=add[o]; 27 int m=l+((r-l)>>1); 28 st[o<<1]+=add[o]*(m-l+1); 29 //左右儿子结点均按照需要加的值总和更新结点信息 30 st[o<<1|1]+=add[o]*(r-m); 31 add[o]=0; 32 //信息传递完之后就可以将父节点的更新信息删除 33 } 34 } 35 36 void update(int o,int l,int r,int ql,int qr,int addv) { 37 //ql、qr为需要更新的区间左右端点,addv为需要增加的值 38 if(ql<=l&&qr>=r) { 39 //与单点更新一样,当当前结点被需要更新的区间覆盖时 40 add[o]+=addv; 41 //更新该结点的所需更新信息 42 st[o]+=addv*(r-l+1); 43 //更新该结点信息 44 return; 45 //根据lazy思想,由于不需要遍历到下层结点,因此不需要继续向下更新,直接返回 46 } 47 48 pushdown(o,l,r); 49 //将当前结点的所需更新信息传递到下一层(其左右儿子结点) 50 int m=l+((r-l)>>1); 51 if(ql<=m)update(o<<1,l,m,ql,qr,addv); 52 //当需更新区间在当前结点的左儿子结点内,则更新左儿子结点 53 if(qr>=m+1)update(o<<1|1,m+1,r,ql,qr,addv); 54 //当需更新区间在当前结点的右儿子结点内,则更新右儿子结点 55 pushup(o); 56 //递归回上层时一步一步更新回父节点 57 } 58 59 ll query(int o,int l,int r,int ql,int qr) { 60 //ql、qr为需要查询的区间 61 if(ql<=l&&qr>=r) return st[o]; 62 //若当前结点覆盖区间即为需要查询的区间,则直接返回当前结点的信息 63 pushdown(o,l,r); 64 //将当前结点的更新信息传递给其左右子节点 65 int m=l+((r-l)>>1); 66 ll ans=0; 67 //所需查询的结果 68 if(ql<=m)ans+=query(o<<1,l,m,ql,qr); 69 //若所需查询的区间与当前结点的左子节点有交集,则结果加上查询其左子节点的结果 70 if(qr>=m+1)ans+=query(o<<1|1,m+1,r,ql,qr); 71 //若所需查询的区间与当前结点的右子节点有交集,则结果加上查询其右子节点的结果 72 return ans; 73 }
2.区间改值
1 // 区间改值(其实只有pushdow函数和update中修改部分与区间加值不同) 2 #include<cstdio> 3 #include<iostream> 4 #include<cstring> 5 #include<cmath> 6 #include<string> 7 #include<algorithm> 8 #include<map> 9 #include<queue> 10 #include<stack> 11 #include<set> 12 #include<vector> 13 typedef long long ll; 14 using namespace std; 15 void pushup(int o){ 16 st[o]=st[o<<1]+st[o<<1|1]; 17 } 18 19 void pushdown(int o,int l,int r){ //pushdown和区间加值不同,改值时修改结点信息只需要对修改后的信息求和即可,不用加上原信息 20 if(change[o]){ 21 int c=change[o]; 22 change[o<<1]=c; 23 change[o<<1|1]=c; 24 int m=l+((r-l)>>1); 25 st[o<<1]=(m-l+1)*c; 26 st[o<<1|1]=(r-m)*c; 27 change[o]=0; 28 } 29 } 30 31 void update(int o,int l,int r,int ql,int qr,int c){ 32 if(ql<=l&&qr>=r){ //同样更新结点信息和区间加值不同 33 change[o]=c; 34 st[o]=(r-l+1)*c; 35 return; 36 } 37 38 pushdown(o,l,r); 39 int m=l+((r-l)>>1); 40 if(ql<=m)update(o<<1,l,m,ql,qr,c); 41 if(qr>=m+1)update(o<<1|1,m+1,r,ql,qr,c); 42 pushup(o); 43 } 44 45 int query(int o,int l,int r,int ql,int qr){ 46 if(ql<=l&&qr>=r) return st[o]; 47 pushdown(o,l,r); 48 int m=l+((r-l)>>1); 49 int ans=0; 50 if(ql<=m)ans+=query(o<<1,l,m,ql,qr); 51 if(qr>=m+1)ans+=query(o<<1|1,m+1,r,ql,qr); 52 return ans; 53 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号