动态规划4.3——最长公共子串问题
题目上添加了超链接,大家点一下题目就会自动跳转到Poj原题界面~~ 冲鸭冲鸭ヾ(◍°∇°◍)ノ゙。
前言:
建议大家按随笔顺序阅览,属于最长序列型动态规划问题的分支,一般操作序列为字符串,占比不大。解题有迹可循,希望大家可以在掌握这四题之后遇到此类问题乱杀。
动态规划组成部分:
1:确定状态
—确定最后一步(最优策略)
—抽象子问题
2:归纳转移方程
3:初始条件和边界情况
4:计算顺序
4.3.1 Common Subsequence (1458)
题意:给定一个序列,取出一些元素(可以不取)后组成一个子序列。序列Z[z1,z2,…,zk]是序列X[x1,x2,…,xm]的子序列,存在一个严格递增的下标序列i1,i2,…ik,使Z中元素和X取下标序列的元素一一对应。给出两个字符串X和Y表示的序列,找出它们最长公共子序列的长度。
小笔记:最长公共子串
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 2005;
int main()
{
char a[N], b[N];
while (~scanf("%s %s", a, b))
{
int la = strlen(a);
int lb = strlen(b);
int c[N][N] = {0};
for (int i = 1; i <= la; i++)
for (int j = 1; j <= lb; j++)
{
if (a[i - 1] == b[j - 1])
c[i][j] = c[i - 1][j - 1] + 1;
else
c[i][j] = max(c[i - 1][j], c[i][j - 1]);
}
printf("%d\n", c[la][lb]);
}
return 0;
}
4.3.2 Palindrome (1159)
题意:一个对称的字符串,从左到右和从右到左读是一样的,称为回文串。给出一个字符串,求最少插入多少个字符可以使它变成一个回文串。
小笔记:比赛里遇到过三次的模板题。
#include <cstdio>
#include <algorithm>
using namespace std;
int main()
{
int n;
char s[5005];
scanf("%d%s", &n, s);
int c[2][5005] = {0};
for (int i = n - 1; i >= 0; i--)
for (int j = i; j < n; j++)
{
if (s[i] == s[j])
c[i & 1][j] = c[(i + 1) & 1][j - 1];
else
c[i & 1][j] = min(c[(i + 1) & 1][j], c[i & 1][j - 1]) + 1;
}
printf("%d", c[0][n - 1]);
return 0;
}
4.3.3 Human Gene Functions (1080)
题意:基因序列可以看成由A,C,G,T组成的字符序列,有一种测量两个基因序列的相似度的方法叫做比对(alignment),在基因对的一个比对可以通过在两个基因序列中插入空格(用减号表示)使两个序列长度相同,接下来通过一个分数矩阵计算出对应位置的分数值。
不同的插入空格方式使得求出来的分数各不相同,将一次比对的各个位置分数求和作为该比对的分数,求不同比对分数中的最大值。
例如两个基因序列为:AGTGATG和GTTAG,插入空格使它们长度相同,一种插入方式是:AGTAAT-G和-GT—TAG,分数矩阵如图所示。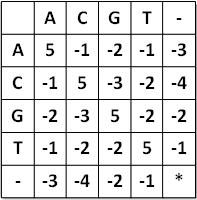
该比对的分数为(-3)+5+5+(-2)+(-3)+5+(-3)+5=9。
另一种:AGTAGTA和-GTTA-G,比对的分数为14。
题解:两个基因序列用字符串A和B表示,数组v保存分数矩阵。
可以使用类似求最长公共子串的方法对两个序列A和B进行分析,用D[i,j]保存计算到A[i]和B[j]时的最大比对分数,D[i,j]有以下3种情况:
①从A中取A[i],在B的此处插入空格;
②从B中取B[j],在A的此处插入空格,;
③从A中取A[i],从B中取B[j]。
取这三种情况的最大值放入D[i+1][j+1]。
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 105;
int v[5][5] =
{
5, -1, -2, -1, -3,
-1, 5, -3, -2, -4,
-2, -3, 5, -2, -2,
-1, -2, -2, 5, -1,
-3, -4, -2, -1, 0};
int main()
{
int s[N];
s['A'] = 0;
s['C'] = 1;
s['G'] = 2;
s['T'] = 3;
int t;
scanf("%d", &t);
while (t--)
{
char A[N], B[N];
int m, n;
scanf("%d %s%d %s", &m, A, &n, B);
int D[N][N];
for (int i = 1; i <= m; i++)
D[i][0] = D[i - 1][0] + v[s[A[i - 1]]][4];//只有情况1
for (int j = 1; j <= n; j++)
D[0][j] = D[0][j - 1] + v[s[B[j - 1]]][4];//只有情况2
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
D[i][j] = max(
max(D[i - 1][j] + v[s[A[i - 1]]][4],
D[i][j - 1] + v[s[B[j - 1]]][4]),
D[i - 1][j - 1] + v[s[A[i - 1]]][s[B[j - 1]]]);
printf("%d\n", D[m][n]);
}
return 0;
}
4.3.4 AGTC (3356)
题意:x和y是包含限定字母的两个字符串,将x转化成y允许的编辑操作包括:
①将一个字符替换成另一个字符;
②插入一个字符;
③删除一个字符。
求将x转化成y最少操作的操作数量。
小笔记:编辑距离。用D[i,j]保存计算到x[i]和y[j]时的最小距离,有以下3种情况:y[j]后插入x[i];将y[j]删除;将y[j]替换为x[i]。
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1005;
int main()
{
int a, b;
char x[N], y[N];
int D[N][N];
while (~scanf("%d %s", &a, x))
{
scanf("%d %s", &b, y);
for (int i = 0; i < N; i++)
D[i][0] = D[0][i] = i;
for (int i = 1; i <= a; i++)
for (int j = 1; j <= b; j++)
{
int u = D[i - 1][j] + 1; //情况①
int v = D[i][j - 1] + 1; //情况②
int w = D[i - 1][j - 1] + !(x[i - 1] == y[j - 1]); //情况③
D[i][j] = min(min(u, v), w); //在3种情况中取最小值
}
printf("%d\n", D[a][b]);
}
return 0;
}


