跳跃表 -- 随机平衡原理
Skip lists are a data structure that can be used in place of balanced trees. Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.
Enhanced LinkedList
要理解SkipList,得先从LinkedList说起,

LinkedList 增删改查的时间复杂度都是O(N),它最大的问题就是通过一个节点只能reach到下一个节点(Doubly LinkedList 是一种改进方案),那么改进的思路就是通过一个节点reach到多个节点,例如下图,

这种情况下便可将复杂度减小为O(N/2)。这是一种典型的空间换时间的优化思路。
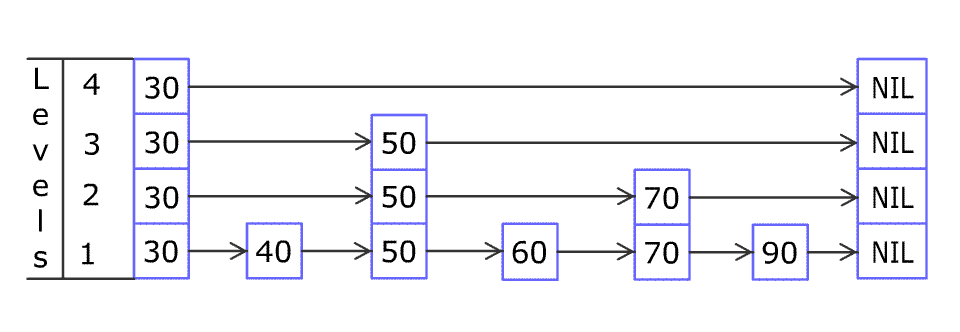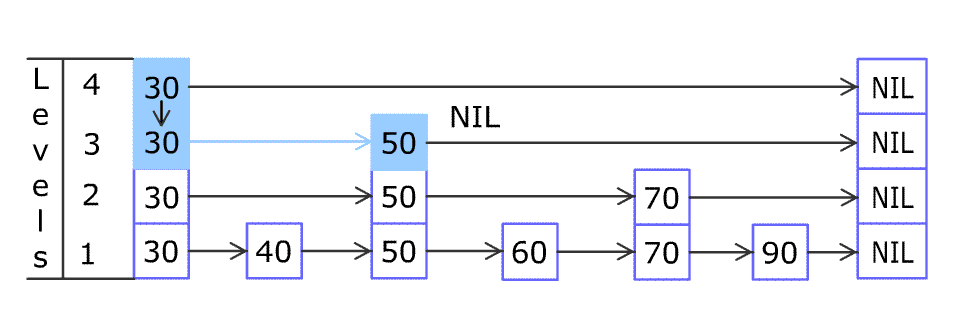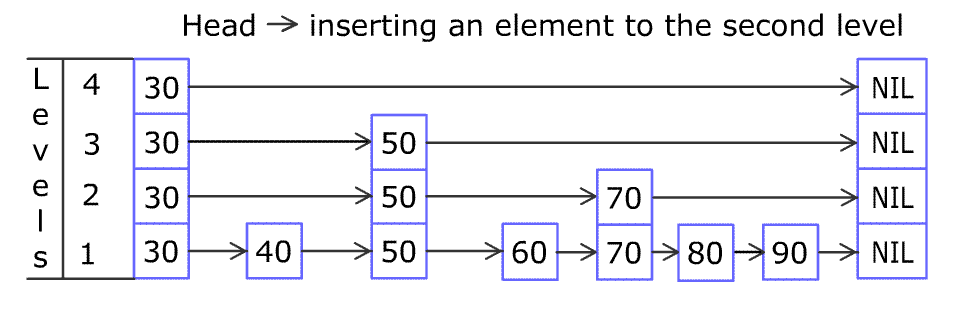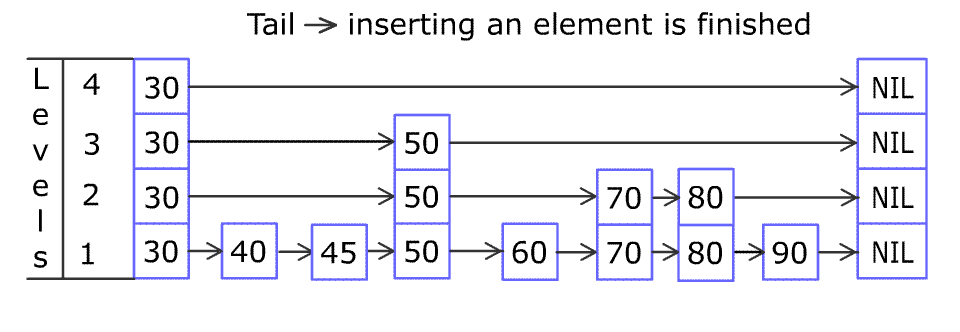
SkipList 更进一步,采用了分治算法和随机算法设计。将每个节点所能reach到的最远的节点,两个节点之间看成是一个组,整个SkipList被分成了许多个组,而这些组的形成是随机的。

(顺时针旋转90度看,SkipList其实更像是一个图结构^_^)
上图中,[3, 6],[6, 25],[25, 26]是三个大组,而在[6, 25]这个组里面又包含了[6, 9],[9, 17],[17, 25]这三个组,其中还继续细分了下去。当你在SkipList中查找某个节点时,很容易就可以跳过某个分组,这样便大大提升了查找效率。这样的分组方式可以实现二分查找。
每个节点所能reach到的最远的节点是随机的,正如作者所说,SkipList使用的是概率平衡而不是强制平衡。
O(logN)?
既然是随机算法,那怎么能保证O(logN)的复杂度?SkipList作者在论文中有给出了说明,这里从另一个角度说下我的理解。先定义一下,A node that has k forward pointers is called a level k node。假设k层节点的数量是k+1层节点的P倍,那么其实这个SkipList可以看成是一棵平衡的P叉树,从最顶层开始查找某个节点需要的时间是O(logpN),which is O(logN) when p is a constant。
下面看下Redis与LevelDB中实现SkipList所使用的随机算法。
Redis
在t_zset.c中找到了redis使用的随机算法。
- /* Returns a random level for the new skiplist node we are going to create.
- * The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
- * (both inclusive), with a powerlaw-alike distribution where higher
- * levels are less likely to be returned. */
- int zslRandomLevel(void) {
- int level = 1;
- while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
- level += 1;
- return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
- }
/* Returns a random level for the new skiplist node we are going to create.
* The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
* (both inclusive), with a powerlaw-alike distribution where higher
* levels are less likely to be returned. */
int zslRandomLevel(void) {
int level = 1;
while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
执行level += 1;的概率为ZSKIPLIST_P,也就是说k层节点的数量是k+1层节点的1/ZSKIPLIST_P倍。ZSKIPLIST_P(这个P是作者论文中的p)与ZSKIPLIST_MAXLEVEL在redis.h中定义,
- #define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */
- #define ZSKIPLIST_P 0.25 /* Skiplist P = 1/4 */
#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */ #define ZSKIPLIST_P 0.25 /* Skiplist P = 1/4 */
所以redis中的SkipList相当于是一棵四叉树。
LevelDB
在skiplist.h中找到了LevelDB使用的随机算法。
- template<typename Key, class Comparator>
- int SkipList<Key,Comparator>::RandomHeight() {
- // Increase height with probability 1 in kBranching
- static const unsigned int kBranching = 4;
- int height = 1;
- while (height < kMaxHeight && ((rnd_.Next() % kBranching) == 0)) {
- height++;
- }
- assert(height > 0);
- assert(height <= kMaxHeight);
- return height;
- }
template<typename Key, class Comparator>
int SkipList<Key,Comparator>::RandomHeight() {
// Increase height with probability 1 in kBranching
static const unsigned int kBranching = 4;
int height = 1;
while (height < kMaxHeight && ((rnd_.Next() % kBranching) == 0)) {
height++;
}
assert(height > 0);
assert(height <= kMaxHeight);
return height;
}
(rnd_.Next() % kBranching) == 0)的概率为1/kBranching,所以LevelDB中的SkipList也是一棵四叉树(kBranching = 4;不就是这个意思吗^_^)。



