三维点云表示

原文链接

点云数据结构

点云数据结构非常简单，只有点的三维坐标信息和法线信息。下面是一个点云表示的抽象类：

    class GPP_EXPORT IPointCloud
    {
    public:
        IPointCloud(){}

        virtual Int GetPointCount() const = 0;
        virtual Vector3 GetPointCoord(Int pid) const = 0;
        virtual void SetPointCoord(Int pid, const Vector3& coord) = 0;
        virtual Vector3 GetPointNormal(Int pid) const = 0;
        virtual void SetPointNormal(Int pid, const Vector3& normal) = 0;
        virtual bool HasNormal() const = 0;
        virtual void SetHasNormal(bool has) = 0;
        
        virtual Int InsertPoint(const Vector3& coord) = 0;
        virtual Int InsertPoint(const Vector3& coord, const Vector3& normal) = 0;
        
        virtual void SwapPoint(Int pointId0, Int pointId1) = 0; 
        virtual void PopbackPoints(Int popCount) = 0;
        virtual void Clear(void) = 0;

        virtual ~IPointCloud(){};
    };

• 点云顶点的存储格式一般是线性的，获取方便，但是删除会存在一些效率问题。IPointCloud提供了SwapPoint函数把需要删除的元素交换到尾部，然后再通过PopbackPoints删除尾部元素.
• Clear函数负责清除Point Coordinate, Point Normal. 回到构造类初始化时的状态.
• HasNormal函数主要用意: 有时候点云创建后没有法线信息，IPointCloud提供这个函数查询点云是否有可靠法线信息. SetHasNormal函数可以设置点云是否有法线信息。

IPointCloud是一个抽象类，不能直接使用。用户可以继承这个接口类，实现其成员函数。这样设计的一个好处是，用户无需改变自己已有的数据结构，只要实现了这个接口类，就可以调用Geometry++里所有关于点云的算法了。真正体现了即插即用的特点。比如用户已经有了一个点云类MyPointCloudData，则我们可以定义一个类MyPointCloud，并用它来调用Geometry++里的各种点云算法：

    class MyPointCloud : public IPointCloud
    {
        MyPointCloudData* mData;
        MyPointCloud(MyPointCloudData* data) : mData(data) 
        {}
        virtual Int GetPointCount() const
        { 
            mData->GetPointCloud(); 
        }
        virtual Vector3 GetPointCoord() const 
        { 
            mData->GetPointCoord(); 
        }
        virtual void SetPointCoord(Int pid, const Vector& coord) 
        { 
            mData->SetPointCoord(pid, coord[0], coord[1], coord[2]); 
        }
        // 其它成员函数类似
    };

    MyPointCloud pointCloud(myPointCloudData); // 用自己的点云数据初始化MyPointCloud
    ErrorCode res = ConsolidatePointCloud::LaplaceSmooth(pointCloud, 0.2, 5); // 调用点云算法API来修改自己的点云数据
    res = ConsolidatePointCloud::CalculatePointCloudNormal(pointCloud);

---

有序点云是什么

一帧扫描数据是一副深度图，属于灰度图。像素的灰度值代表的是深度信息，可以通过相机参数把每个像素点变换到世界坐标系，这样每个像素就对应一个三维点，有些点是无效的。下图是一个典型的深度点云。

有序点云是一个方阵，如图所示。点云按照方阵一行一行的，从左上角到右下角排列。

---

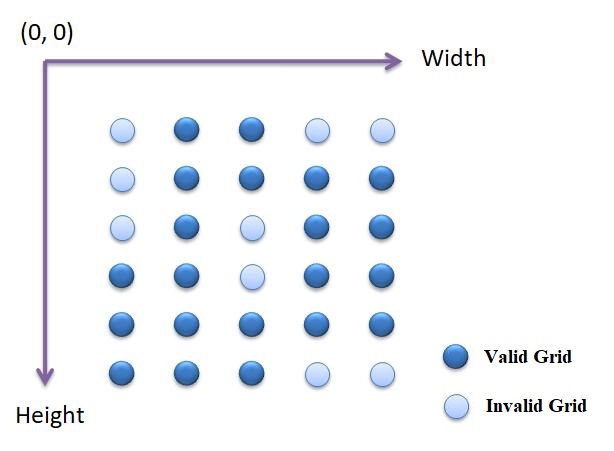
有序点云到无序点云遗失了哪些信息

• 有序点云按顺序排列，可以很容易的找到它的相邻点信息。
• 无效点信息也有用，可以通过它快速准确的找到点云边界。
• 有序点云一般是在相机坐标系里的，所以法线是面向相机的，所以法线定向问题自然就解决了。如果曲面几何是光滑变化的，还可以应用法线的Z分量来定义点云的边界。如下图所示，颜色代表了法线Z分量。有些扫描仪在边界处的误差比较大，可以用这个方法很快速准确的去掉边界处的点。

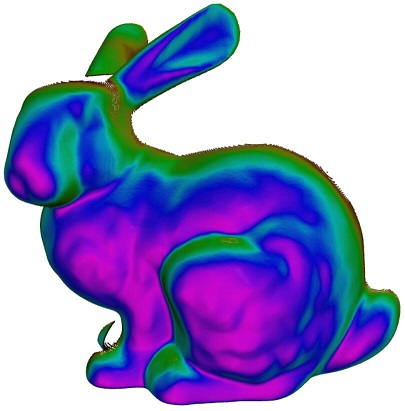
与无序点云相比，有序点云的处理速度可以快很多。