基于统计的无词典的高频词抽取(一)——后缀数组字典序排序

中文全文检索中很重要的一个环节就是分词，而一般分词都是基于字典的，特别是对于特定的业务，需要从特定的语料库中抽出高频有意义的词来生成字典。这系列文章，就一步一步来实现一个从大规模语料库正抽取出高频词的程序。

抽词的过程如下图：

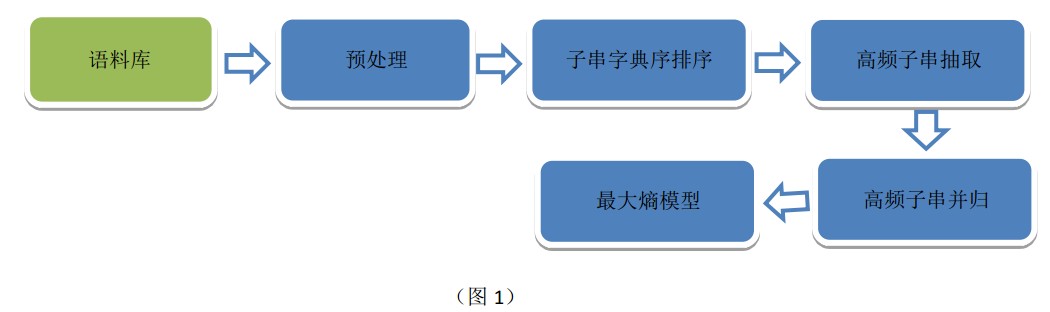
本文先讲解“子串字典序排序”部分，也就是字典序排序部分。本文使用两种算法：快排 和 基数排序，两种算法各有应用场景，快排在分析长度20万字符串时所用的时间明显低于基数排序，但是，超过时，基数排序明显有优势；本文仅仅对于实现的算法做简单分析和实现，真正生成环境中，将引入多线程，分布式处理等优化手段，这里不提及。

这里，我要先用通俗一些的话语来解释一些概念，有不正确的地方，欢迎指出；

字典序：字典序是按照字符的顺序来排序。例如，‘a’跟‘b’,则字典序为： ‘a’，‘b’；“adc”跟“acd”的字典序为：“acd”，“adc”。

子串：假设现在有字符串S：“S₁S₂S₃…S_n-1S_n”,如果存在i≥1且j≤n（i≤j）, 则“S_iS_i+1…S_j-1S_j”为S的子串。

后缀数组：后缀树的代替方案；后缀是指从某个位置 i 开始到整个串末尾结束的一个特殊子串。字符串r的从 第 i 个字符开始的后缀表示为 Suffix(i) ，也 就是Suffix(i)=r[i..len(r)]。而后缀数组则是记录开始位置i的一个数组。

PAT数组：主要用于对文本进行全文索引；PAT数组是一个字符串的后缀树的字典序的排列。

LCP数组：对应一个PAT数组，表示PAT数组间相邻的两个后缀子串的最长公共前缀。

（注，PAT和LCP两个概念相当重要）

【例】有字符串“abcba”，则其后缀树为{“abcba”,“bcba”,“cba”,“ba”,“a”},

后缀数组为：{0,1,2,3,4},字典序排序后为：{“a”,“abcda”,“ba”,“bcba”,“cba”},

PAT为：{4,0,3,1,2}, LCP:{1,0,1,0,0}

从例子可以知道，子串字典序排序的问题可以分解为，求后缀数组，后缀数组字典序排序两个子问题。

获取后缀数组是一种特殊的子串集合，相当容易获取，这里就不累赘。

1. 使用快排来实现后缀数组排序（不重点讲解，重点讲解基数排序）：

public static void DictSort(int[] a, string s, int left, int right) 
{
    while (left < right) 
    {
        int i = Partition(a, s, left, right);
        DictSort(a, s, left, i - 1);
        left = i + 1;
    }
}
                                
public static int Partition(int[] a, string s, int left, int right) 
{
    var _tmp = a[left];
    string tmp = s.Substring(a[left]);
    while (left < right) 
    {
        while (left < right && s.Substring(a[right]).CompareTo(tmp) >= 0)
            right--;
        if (left < right)
            a[left] = a[right];
        while (left < right && s.Substring(a[left]).CompareTo(tmp) <= 0)
            left++;
        if (left < right) 
        {
            a[right] = a[left];
            right--;
        }
    }
    a[left] = _tmp;
    return left;
}

其中，a为后缀数组，s为源字符串。程序执行完后，a为PAT数组。

2. 使用基数排序来排序后缀数组：

使用该算法的先决条件：输入的可枚举，即有限的集合中。而因为汉字跟英文字母可以枚举

基数排序：也叫“木桶排序”，是一种分配式排序。时间复杂度为O(nlog(r)m)，其中r为所采取的基数，而m为堆数。

【例子】假设现在有“1”，“15”，“26”，“55”，“10”这5个数，进行基数排序过程如下：

Step 1： 将个位数放进相应的位置（如下图）

Step 2， 从0到9依次读出该数组：10,1,15,55,26

Step 3： 根据Step 2 的结果，再进行一次对十位数的排序（如下图），【注：“1”=“01”】：

Step 4： 再执行一次Step 2，得到“1”，“10”，“15”，“26”，“55”，结束。

要将该算法运用到字符串中，我们首先得对字符进行编码：

1. 字符串编码映射

用整型来表示编码，对于GB2312编码，有7445个字符，其中6763个汉字和682个其他字符。汉字的内码范围高字节B0-F7，低字节A1-FE。则映射公式可表示为：

Code = (High-176)*94+(Low-161)+Δ；

然而，对于很多应用来说，GB2312编码不够用，因为存在一些繁体字，生僻字等未收录到GB2312编码中，所以我们采用GBK编码，GBK共可以表示23940个字符，其中21003个汉字，映射公式可以表示为：

Code =（Heigh-129）*94+(Low-64)+ Δ；

代码如下：

public static int[] GetGBCode(string s) 
{
    int len = s.Count();
    int[] gbCode = new int[len];
    Encoding chs = Encoding.GetEncoding("GBK");
    for (var i = 0; i < len; i++) 
    {
        byte[] bytes = chs.GetBytes(s[i].ToString());
        if (bytes.Length == 1)
            gbCode[i] = bytes[0];
        else
            gbCode[i] = (bytes[0] - 129) * 94 + (bytes[1] - 64);
    }
    return gbCode;
}

2. 用基数排序来排序编码后的字符串：

【例】输入为“张则智”，“是个天才”，“绝对天才”：

Step 1：映射编码（如下图）

Step 2： 我们从最后一个字符开始进行基数排序【注：空字符为0】

Sort 1： 张则智，是个天才，绝对天才

Sort 2：是个天才，绝对天才，张则智

Sort 3：绝对天才，是个天才，张则智

Sort 4：绝对天才，是个天才，张则智

排序结束；也就是说，我们需要进行输入串S.Lengh次线性排序。

代码片段1：

public static void RadixSort(int[, ] A, int[] B, int t, int n, int M) 
{
    int[] C;
    for (int k = n - 1; k >= 0; k--) 
    {
        C = new int[M];
        for (int i = 0; i < n; i++) 
        {
            C[A[i, k]]++;
        }
        for (int m = 1; m < M; m++) 
        {
            C[m] += C[m - 1];
        }
        for (int j = 0; j < n; j++) 
        {
            B[--C[A[j, k]]] = j;
        }
    }
}

上述代码段，简单易理解，但是有个问题，当输入过大时，A这个二维数据太大，会导致内存泄露，所以，进行了改进：

代码片段2：

public static void RadixSort(int[] A, int[] B, int t, int n, int M) 
{
    int[] C;
    int[] tmp = new int[t];
    for (var x = 0; x < t; x++) 
    {
        tmp[x] = x;
    }
    for (int k = n - 1; k >= 0; k--) 
    {
        C = new int[M];
        for (int i = 0; i < n; i++) 
        {
            int z = k + tmp[i];
            if (z <= t - 1) 
            {
                C[A[z]]++;
            } 
            else 
            {
                C[0] += n - i;
                break;
            }
        }
        for (int m = 1; m < M; m++) 
        {
            C[m] += C[m - 1];
        }
        for (int j = 0; j < n; j++) 
        {
            int u = k + tmp[j];
            if (u <= t - 1)
                B[--C[A[u]]] = j;
            else 
            {
                for (int y = j; j < n; j++) 
                {
                    B[--C[0]] = j;
                }
                break;
            }
        }
    }
}

程序2做了优化，其中A为对应的编码，B为后缀数组，t为后缀数组的长度，n为字符串的长度，M为GBK中汉字的个数（本应用中）。

当语料库增长到百万级别后，平均花费时间明显低于快排。

两个算法可以使用多线程来进行分块排序在合并，此处未做这方面的优化。

好了，第一部分就先讲到这里，如果觉得文章对您有用或者对其他人有帮助，请帮忙点文章下面的“推荐”；如果文章有任何纰漏，欢迎指正，谢谢！