动态规划学习笔记

一.动态规划的含义

动态规划是用来解决一类最优化问题的算法。它将一个复杂的问题分解成若干个子问题，通过综合子问题的最优解来得到原问题的最优解。为提高动态规划的效率，还需要将每个子问题的最优解记录下来，省去不必要的重复计算。

二.动态规划的两种写法

递归写法：

典型的例子就是斐波那契数列，定义为：F(0)=F(1)=1，F(n)=F(n-1)+F(n-2)（n不小于2）。递归写法如下：

int F(int n){
    if(n == 0 || n == 1) return 1;
    else return F(n - 1) + F(n - 2);
}

这样将一个较大的整数不断分解成若干个小的整数，从而求出解。但在这个过程中，有些整数的值可能会被重复计算，例如求解F(5)时，会分解成求解F(4)和F(3)的值，而求解F(4)时又会去求F(3)的值，为了避免重复计算，可用一个一维数组dp，用来保存已经计算过的结果，其中dp[n]记录的就是F(n)的结果，因此代码修改如下：

int dp[maxn] = {0};

int F(int n){
    if(n == 0 || n == 1) return 1;
    if(dp[n] != 0) return dp[n];
    else{
        dp[n] = F(n - 1) + F(n - 2);
        return dp[n];
    }
}

递推写法：

以数塔问题为例，如下图所示，将一些数字排成数塔形状，其中第一层有一个数字，第二层有两个数字……第n层有n个数字。现在要从第一层走到第n层，每次只能走向下一层连接的两个数字中的一个，求最后将路径上所有数字相加后得到的和最大是多少？

 

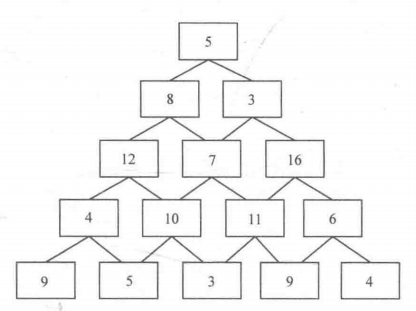
 如果采用暴力解，穷举所有路径情况，然后筛选出最大值，那么时间复杂度为O(2^n)，当n很大时就会超时，所以必须采用动态规划的方式来解决这个问题。

先将所有的数字存入二维数组f中，即f[i][j]表示第i层第j个数字，在上图中就是f[1][1]=5，f[2][1]=8，……，f[5][5]=4。再开一个二维数组来记录每个子问题的最优解，即二维数组dp，其中dp[i][j]代表第i层第j个数字到达底层的最优解，由此可以得出一个关键等式，状态转移方程：

dp[i][j]=max(dp[i+1][j], dp[i+1][j+1])+f[i][j]

其中max表示两者中的较大值。那么再考虑边界问题，当来到了最底层，即i=n时，此时每个元素走到最底层的路径就是元素的本身数字，即有

dp[n][j]=f[n][j]（1≤j≤n）

因此数塔问题的代码如下：

#include <stdio.h>
#include <algorithm>

using namespace std;

int main(){
    int n;
    while(scanf("%d", &n) != EOF){
        int f[n][n], dp[n][n];
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= i; j++){
                scanf("%d", &f[i][j]);
            }
        }
        for(int j = 1; j <= n; j++){
            dp[n][j] = f[n][j];
        }
        for(int i = n - 1; i >= 1; i--){
            for(int j = n - 1; j >= 1; j--){
                dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + f[i][j];
            }
        }
        printf("%d", dp[1][1]);
    }
    return 0;
}

再看另外一个例子：最大连续子序列。给定一个数字序列A1，A2，……，An，求i，j（1≤i≤j≤n），使得Ai+……+Aj最大，输出这个最大和。

样例：

输入：
-2 11 -4 13 -5 -2
输出
20

　　样例解释：

11+(-4)+13=20为和最大的选取情况

同样的先来看暴力解，枚举左右端点i、j，需要O(n^2)的复杂度，再计算Ai+……+Aj需要O(n)的复杂度，所以总复杂度为O(n^3)，如采用上述方法记录每个子问题的解，使计算时间变为O(1)，也仍然需要O(n^2)复杂度，也会有超时的可能性。

因此用动态规划来解这个问题，一维数组dp存储着每个子问题的最优解，即dp[i]表示以A[i]结尾的最大连续序列和，那么初始情况为

dp[0]=A[0]

而关键的状态转移方程为

dp[i]=max(A[i], A[i]+dp[i-1])

只需要一次循环遍历，就能得出A[n]数组中所有元素为结尾的最大连续序列和，时间复杂度降低到了O(n)。

#include <stdio.h>
#include <algorithm>

using namespace std;

const int maxn = 10010;

int main(){
    int n;
    int A[maxn], dp[maxn];
    while(scanf("%d", &n) != EOF){
        for(int i = 1; i <= n; i++){
            scanf("%d", &A[i]);
        }
        dp[1] = A[1];
        int ans = dp[1];
        for(int i = 2; i <= n; i++){
            dp[i] = max(A[i], dp[i - 1] + A[i]);
            if(dp[i] > ans) ans = dp[i];
        }
        printf("%d", ans);
    }
    return 0;
}

三.总结

因此，动态规划问题的核心，就是划分复杂问题为容易解决的子问题，并给出每一层问题划分的状态转移方程。如何设计状态和状态转移方程，这才是动态规划最难的地方。