详解动态规划(Dynamic Programming)& 背包问题
详解动态规划(Dynamic Programming)& 背包问题
引入
有序号为1~n这n项工作,每项工作在Si时间开始,在Ti时间结束。对于每项工作都可以选择参加与否。如果选择了参与,那么自始至终都必须全程参与。此外,参与不同工作的时间段不能重叠。目标是参与尽可能多的工作,问最多能参与多少项工作?
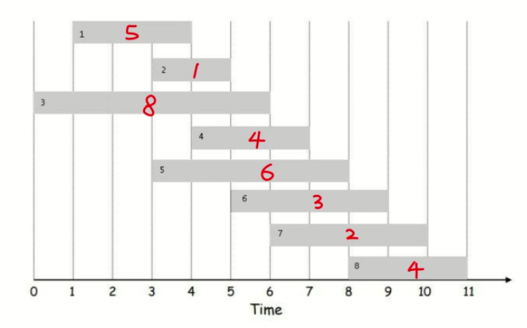
这个问题乍一看有点棘手,由于每项工作间有时间段的重叠问题,而导致可能选了某个工作后接下去的几个选不了了。所以并不是简单地从起始时间开始,每次在可选的工作中选最早遇上的会达到最优。
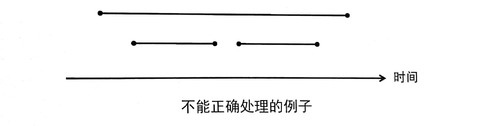
事实上,不从遍历时间,而从遍历工作的角度上会更容易想到,每项工作其实都只有选和不选的区别。划分子问题就是这类题目最主要的思想。对于选和不选两种情况,可以分解为仅由余下工作所构成的同样的子问题。
假设用OPT(i)来表示在这1~i个工作中最多能参与多少项。那么对于当前的第i个工作:
- 如果选。则有 OPT(i) = 1 + OPT(pre[i]) // pre[i]表示第i个工作之前,离它最近的可选工作的序号(可以直接预处理出来)。
- 如果不选。则 OPT(i) = OPT(i-1) // 简单地去掉这个第i项即可
然后在选与不选的两种情况中取最优。
int OPT(int i)
{
if(i == 0) return 0;
return max(OPT(i-1), 1+OPT(pre[i]));
}
但这里会有个问题,这个递归可能会反复的计算某个值(比如下图中的OPT(5)),浪费了很多时间。这也就是重叠子问题(overlap sub-problem),解决方案是用数组存下每次计算的答案,下次如果再要计算时直接用先前保留好的值就行(称为记忆化搜索)。

int OPT(int i)
{
if(i == 0) return 0;
if(dp[i] != 0) return dp[i];
return dp[i] = max(OPT(i-1), 1+OPT(pre[i]));
}
由于明显可以看出来这是一个从前往后更新的状态,每个OPT[i]都取决于它之前的值,所以也可以直接用一个for遍历更新,这样做更简洁。
dp[0] = 0;
for(int i = 1; i <= n; i++)
dp[i] = max(dp[i-1],1+dp[pre[i]);
这种一步步按顺序求出问题的解的方法称作动态规划,不熟练DP的时候可以先从记忆化搜索出发推导出递推式。
其实这道题还可以用贪心的思路解决,正确的贪法是每次选取结束时间最早的工作。证明大概是,这个方案在选取了相同数量的更早开始的工作时,最终结束时间不会比其他方案的更晚,所以不存在选取更多工作的方案。(严格意义的证明需要归纳法和反证法)
但个人感觉贪心总是很玄学,能把动规想清楚就还是稳妥的动规吧。
题目二
给出一组正整数,问能不能取出任意个求和恰好为S。如果能的话返回Ture,不能返回False。

同样的从“取和不取”的角度来考虑。如果用OPT(i,S)来表示从1~i这前i个数中去凑S的话:
- 选第i个。OPT(i,S) = OPT(i-1,S-arr[i])
- 不选第i个。OPT(i,s) = OPT(i-1,S)
最终返回的是OPT(i-1,S-arr[i]) || OPT(i-1,S)
这里出口的判断值得注意:
如果S为0,说明已经凑好了不需要再取了,直接返回true。
如果S不为0且i为0,这时已经没有办法凑了,直接返回false。
并且还有一个难想到的点,如果arr[i]>S,那么只能走不选的分支。
bool OPT(int i, int S)
{
if(S == 0) return true;
if(i == 0) return false;
if(arr[i] > S) return OPT(i-1,S);
return OPT(i-1,S-arr[i]) || OPT(i-1,S);
}
同样的可以记忆化搜索开个dp数组存一下提高效率。
或者这里用另一种方法,直接非递归的遍历更新。
for(int s = 0; s <= S; s++) dp[0][s] = false;
for(int i = 0; i <= n; i++) dp[i][0] = true;
for(int i = 1; i <= n; i++)
for(int s = 1; s <= S; s++)
{
if(arr[i] > s) dp[i][s] = dp[i-1][s];
else dp[i][s] = dp[i-1][s-arr[i]] || dp[i-1][s];
}
背包问题
01背包
有n个重量和价值分别为w[i]、v[i]的物品,从这些物品中挑选出总重量不超过W的物品,问所有挑选方案中价值总和的最大值。
用dp[i][j]来表示对于1~i这前i个物品,装入容量为j的背包中的最大价值。则有:
- dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]]+v[i])
- 当 j < w[i] 时,只能走不选的分支 dp[i][j] = dp[i-1][j]
初始化时对于i=0及j=0时,dp值都为0。
for(int i = 1; i <=n; i++)
for(int j = 1; j <= W; j++)
{
if(j < w[i]) dp[i][j] = dp[i-1][j];
else dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]);
}
return dp[n][W];
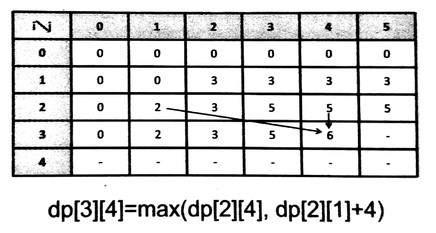
实际上,dp[i][j] 的值只依赖于第 i−1 行的 dp[i−1][0...j] 这前 j+1 个元素,与 dp[i−1][j+1...W] 的值无关。所以其实只存1行就能完成整个dp过程。
用 dp[0...W] 存储当前行,更新 dp[0...W] 的时候,按照 j=W...0 的递减顺序计算 dp[j],这样可以保证计算 dp[j] 时用到的 dp[j] 和 dp[j−w[i]] 的值和原本的二维数组中的第 i−1 行的值是相等的。更新完 dp[j] 的值后,对 dp[0...j−1] 的值不会产生影响。并且只需要更新到 j=w[i] 就可以停止,因为再之前的与第 i−1 行没有变化。
for(int i = 1; i <= n; i++)
for(int j = W; j >= w[i]; j--)
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
return dp[W];
完全背包
有n种重量和价值分别为w[i]、v[i]的物品,从这些物品中挑选出总重量不超过W的物品,问所有挑选方案中价值总和的最大值。每种物品可以挑选任意多件。
与01背包唯一的不同就是从“选和不选”变成了“选几件”。
用dp[i][j]来表示对于1~i这前i个物品,装入容量为j的背包中的最大价值。对于第i件物品,至多可以选k件,其中k满足k*w[i] <= j。
于是把上面的代码改一改可以写成三重循环:
for(int i = 1; i <=n; i++)
for(int j = 1; j <= W; j++)
for(int k = 0; k*w[i] <= j; k++)
dp[i][j] = max(dp[i][j], dp[i-1][j-k*w[i]] + k*v[i]);
但事实上,对于dp[i][j]中选k个的情况,和dp[i][j-w[i]]选k-1个是一样的。也就是说,仍然能当做选与不选两种情况,只是如果选了,i的位置没有改变(此位置的物品是无尽的)。
则有:
- dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]]+v[i])
- 当 j < w[i] 时,只能走不选的分支 dp[i][j] = dp[i-1][j]
for(int i = 1; i <=n; i++)
for(int j = 1; j <= W; j++)
{
if(j < w[i]) dp[i][j] = dp[i-1][j];
else dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]] + v[i]);
}
return dp[n][W];
同样的,可以简化为只用一维数组,在这里需要用之前第 i−1 行的值只有当前这一个dp[i-1][j],而需要用到更新后的第i行的值却是dp[i][0...j],所以遍历时得从前往后更新。同样的,只需从 j=w[i] 开始,因为与之前没有变化。
for(int i = 1; i <= n; i++)
for(int j = w[i]; j <= W; j--)
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
return dp[W];
一道变形
You are given a list of non-negative integers, a1, a2, ..., an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.
Find out how many ways to assign symbols to make sum of integers equal to target S.
Example 1:
Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
There are 5 ways to assign symbols to make the sum of nums be target 3.
Note:
The length of the given array is positive and will not exceed 20.
The sum of elements in the given array will not exceed 1000.
Your output answer is guaranteed to be fitted in a 32-bit integer.
如果暴力搜索的复杂度是O(2^n),然而巧妙的化简一下就能变成DP。
关键就在于这三步推导:
sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
2 * sum(P) = target + sum(nums)
从而题目就变为了找一个子序列P使得 sum(P) = (target + sum(nums)) / 2 成立,也由此得知target + sum(nums)必须为偶数。
想起有另一道类似题Partition Equal Subset Sum,题意是找出两个和相等的子序列。也即能否找到一个子序列,使得和为整个数组和的一半,然后就是0-1背包问题。
bool canPartition(vector<int>& nums) {
int sum = 0;
for(auto e : nums) sum += e;
if(sum%2 != 0) return false;
sum/=2;
bool dp[20001] = {0};
dp[0] = true;
for(int i = 0; i < nums.size(); i++)
for(int j = sum; j >= nums[i]; j--)
dp[j] = dp[j] || dp[j-nums[i]];
return dp[sum];
}
于是本题的代码就很容易写了,把上面代码改一改,dp存的不再是“是否能装下”,而是“能装下的方案数”,表达式改为 dp[j] += dp[j-nums[i]]
int subsetSum(vector<int>& nums, int sum) {
int dp[20001] = {0};
dp[0] = 1;
for(int i = 0; i < nums.size(); i++)
for(int j = sum; j >= nums[i]; j--)
dp[j] += dp[j-nums[i]];
return dp[sum];
}
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for(int i = 0; i < nums.size(); i++) sum += nums[i];
if((S+sum)%2 != 0 || sum < S) return 0;
return subsetSum(nums,(S+sum)/2);
}


