浅尝狭义相对论

小引

由于，某天有位物竞同学在群里发了道 \(Lorentz\) 变换的题，本着求知精神（bushi，我花了一天时间搞了搞。但是，教学里充斥的悖论（佯谬）实在让人糊涂，就又花了一天把狭义相对论看了看。但也仅止步于与洛伦兹变换相关的内容，没有深入，仅了解了足够解释悖论的内容。

由于参考资料不够，部分内容为自己手推猜测，内容可能存在错误（还有，原谅我糟糕的手绘。

正文

从伽利略变换到洛伦兹变换

伽利略变换如下：

\[x'=x-ut\\ y'=y\quad z'=z\\ t'=t \]

是一种转换参照系的方程，默认时间不变。

然而这时出现了问题，详见 迈克尔逊-莫雷实验 ，此实验说明光速对于任何参照系的观察者来说不变。

依据伽利略变换来说肯定是有问题的。

洛伦兹认为，这是因为改变参照系时，尺长和时间出现一定改变。

所以他引入一个因子 \(\gamma\) ，与速度有关，代表尺长的改变比例，即：

\[x'=\gamma(x-ut)\\ x=\gamma(x+ut) \]

并通过联立解出 \(t\) 的变换式：

\[t'=\gamma(t+\frac{(1-\gamma^2)x}{u\gamma^2})\\ t=\gamma(t'-\frac{(1-\gamma^2)x'}{u\gamma^2}) \]

此时，假设一人在运行的火车车尾，发射一光脉冲引爆车头一装置，车长 \(x\) ，历时 \(t\) 。

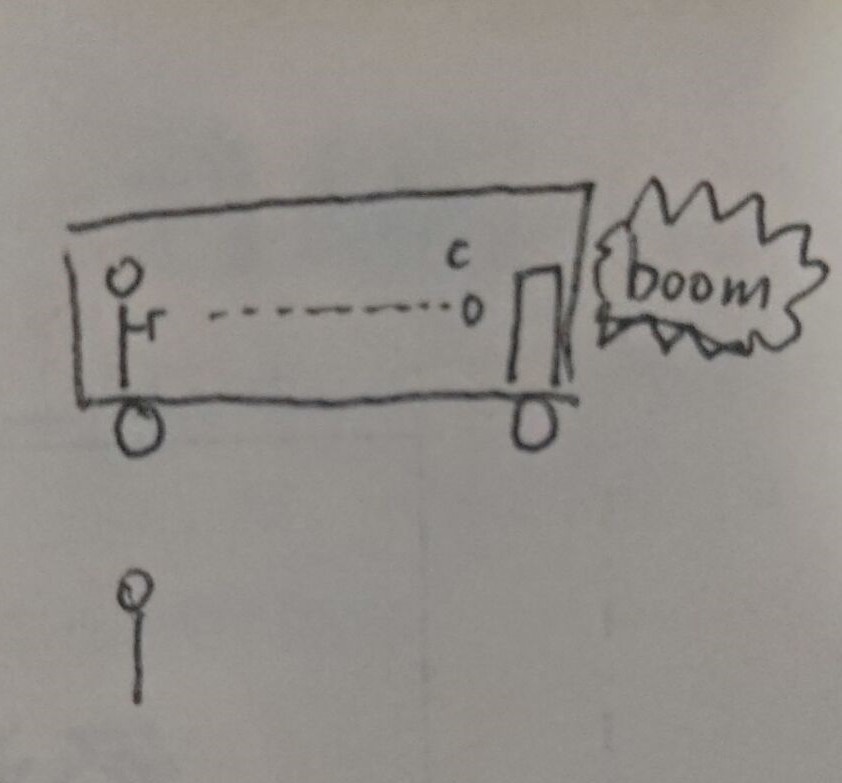
又有一人在地面观测到此过程历时 \(t'\) 。因为光速不变，车内观测的距离是 \(x=ct\) ，而车外观测的距离是 \(x'=ct'\) 。这样就有一个关于 \(x'\) 和 \(t'\) 的方程，即可解出 \(\gamma\) 。

\[\begin{cases} x'=\gamma(x-ut)\\ t'=\gamma(t+\frac{(1-\gamma^2)x}{u\gamma^2})\\ x'=ct'\\ x=ct\\ \end{cases} \\ \bf 解得：\\\rm \gamma^2=\frac{c^2t}{c^2t-u^2t}\implies \gamma=\frac{1}{\sqrt{1-(\frac{u}{c})^2}} \]

我们一般设 \(\beta=\frac{u}{c}\) ， \(\gamma=\frac{1}{\sqrt{1-\beta^2}}\) 。将洛伦兹变换表示为：

\[x'=\gamma(x-ut)\\ y'=y\quad z'=z\\ t'=\gamma(t-\frac{u}{c^2}x) \]

两参照系的相对速度互为负值，所以反变换的式子只需将上式中 \(u\) 前加个负号即可。

而在实际问题中，我们经常讨论的差值，即变化量来说：

\[\Delta x'=\frac{\Delta x-u\Delta t}{\sqrt{1-(\frac{u}{c})^2}}\\ \Delta t'=\frac{\Delta t-\frac{u}{c^2}\Delta x}{\sqrt{1-(\frac{u}{c})^2}} \]

而两式只商为：

\[\frac{\Delta x'}{\Delta t'} = \frac{\Delta x-u\Delta t}{\Delta t-\frac{u}{c^2}\Delta x} \]

取极限即为速度的变换式，但是右式我们并不好直接取，可以对右式上下同除一个 \(\Delta t\) 再取，得：

\[v'=\frac{v-u}{1-\frac{u}{c^2}v}\\ v=\frac{v+u}{1+\frac{u}{c^2}v} \]

这即是佐证光速不变和光速是极限速度的式子。可以发现，将小于光速的速度叠加，将永远小于光速。

而将 \(c\) 代入，结果永远是 \(c\) 。

同时性

将时间作为坐标，兆示着 同时 这个概念不再严谨，譬如在参照系 \(S\) 中的事件 \((x_1,0),(x_2,0)\) （由于 \(y,z\) 在变换中没有改变，我们只讨论 \(x,t\)） 。

转换至 \(S'\) 时：

\[t'= \gamma(t-\frac{u}{c^2}x) \]

两者的 \(x\) 有差异，致使 \(t'\) 不相同。于是，在 \(S'\) 中两事件就不是同时发生的。

钟慢效应

即为：时钟在静止的参照系中最快。

注意时间间隔的洛伦兹变换式为：

\[\Delta t'=\frac{\Delta t-\frac{u}{c^2}\Delta x}{\sqrt{1-(\frac{u}{c})^2}}\\ \Delta t=\frac{\Delta t'+\frac{u}{c^2}\Delta x'}{\sqrt{1-(\frac{u}{c})^2}} \]

下面的分母必然小于 \(1\) 所以转换出来的 \(\Delta t'\) 必然大于 \(\Delta t\) ，意思是，在你看来，对方觉得一秒内的事情你觉得过了更长时间，即为对方的表慢了。有趣的是，由 \(\Delta t'\) 转向 \(\Delta t\) 也会出现相同情况。就成了互相看对面钟慢的局面。

注意，这里是指时间间隔大，意思是说，最明显的表现是表慢了，但其实万物的推进速度都会变慢。

至于这两者的互相矛盾，其实并不。两者只是观察角度不同，在两个参照系下，各自都是正确的。正如两个人互相远离后，都可以对对方说，“嘿，你看起来变矮了”。

借用耶鲁大学某教授神奇比喻：

” In fact,even more paradoxical is how in this world two people can simultaneously look down on each other“

事实上，更悖论的是世界上可以存在两人同时互相看不起对方。

尺缩效应

即为：米尺在静止的参照系中最长。

如何量取一个物品的长度呢，当然是 同时 截取其首尾，计算坐标差。

已知坐标间隔的洛伦兹变换为：

\[\Delta x'=\frac{\Delta x-u\Delta t}{\sqrt{1-(\frac{u}{c})^2}}\\ \Delta x=\frac{\Delta x'+u\Delta t'}{\sqrt{1-(\frac{u}{c})^2}} \]

因为必须同时测量， \(\Delta t\) 就为 \(0\) 那么就变成了：

\[\Delta x'(\sqrt{1-(\frac{u}{c})^2})=\Delta x \]

既然 \(\Delta t\) 为 \(0\) ，那么 \(\Delta x\) 就是你所观测到的长度，由于根号下的数小于 \(1\) ，你所见的杆长会小于对面的。

两个悖论

• 假设 \(A\) 以一个极高的速度与 \(B\) 擦肩而过，这个速度使得尺缩为原来的一半。那么这时，\(A\) 手上有个半米长的洞，\(B\) 手上有个一米长的尺子。那么，在 \(A\) 看来，尺子可以进去，在 \(B\) 看来，一米的尺子当然进不去四分之一米的洞。然而即使两者的观察角度不同，尺能否进去的答案只能有一个，到底是能进去还是不能呢？

  

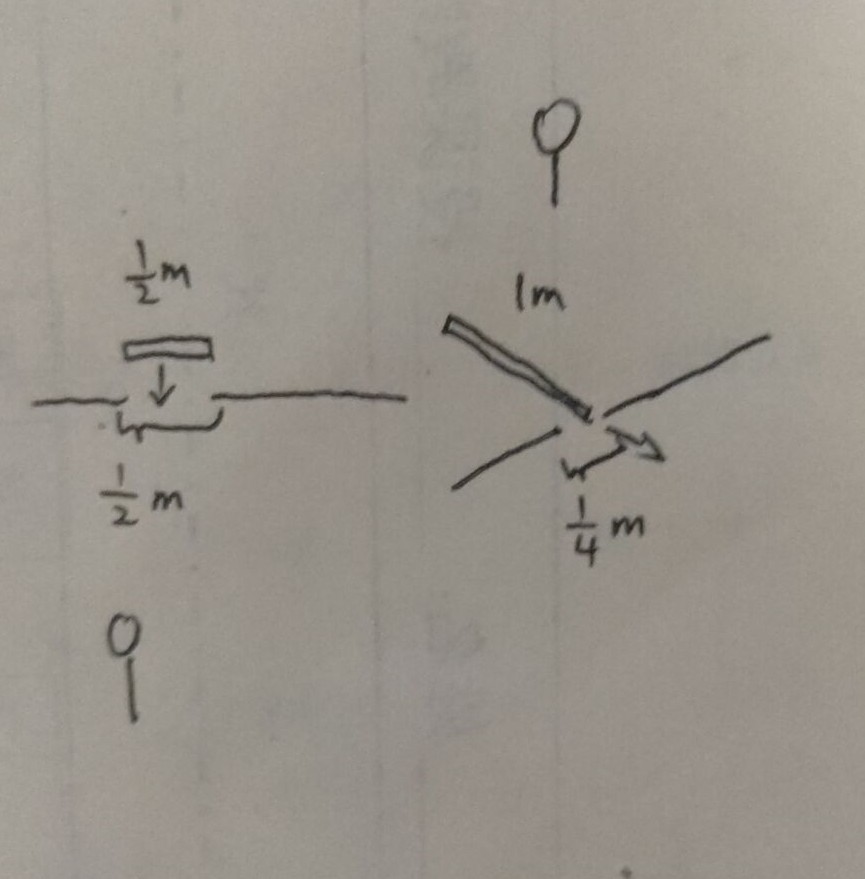
  答案是能进去。

  这个佯谬的关键在于同时性，也解释了尺缩的本质。在你眼里，你是同时量的尺子两端，尺子也是两端同时进去。而在对方眼里，你不是同时量的尺子，而尺子是一头先进洞，然后另一头再进去的。

• 双生子悖论

  假设有一对双生子，哥哥坐上火箭，高速远离地球再回来，而弟弟在地球上。按钟慢效应，哥哥会觉得弟弟年轻，弟弟会觉得哥哥年轻。然而两人中只有一人会更年轻，到底谁是对的呢。

  这个悖论在于，题中忽略了加减速阶段，狭义相对论只适用于惯性系，加减速是非惯性系，所以要用广义相对论。

  但是其实用狭义相对论也可以解释，解决方法就是闵氏时空。

  P.S. 在了解过程中发现了这个整活视频 。

闵可夫斯基时空

又称闵氏时空。将时间这一维加入坐标系来描述。

然而已经有三个正交轴了，剩下的时间轴塞哪呢。

于是乎我们将时间乘上 \(ic\) ，即以 \(ict\) 作为第四轴，这样既与三个轴正交，又解决了单位问题。（\(i\) 为虚数单位，\(c\) 为任意速度，当然根据事实是光速，这个稍后解释）。

由洛伦兹变换式可知，洛伦兹变换是个线性变换，放在闵氏时空里，就是一个坐标系转动。

距离

在坐标系变换中，我们首先要找到一个不变量，这个量就是距离 \(s\) 。

既然是距离，那么当然是用类似勾股的方法，将平方加起来就好了：

\[s^2=|x^2+y^2+z^2+(ict)^2|\\ =|r^2-c^2t^2| \]

并且定义固有时 \(\tau=\frac{\Delta s}{c}\) ，由于各参照系中距离是不变的，固有时就统一了不同参照系的时间。

并且此时，\(c\) 就成了宇宙中的一个特殊的速度。

若一物体在参照系 \(S\) 中以 \(c\) 移动，其 \(\frac{\Delta r}{\Delta t}\) 值为 \(c\) ，即 \(\Delta r=c\Delta t\) ，这样 \(s\) 就为 \(0\)。

那么在任意参照系中 \(s'\) 也为 \(0\) ，那么其速度也是 \(c\) 。（不管 \(c\) 是不是光速）

那么根据事实得知的光速不变原理，我们将其认为是光速。

复坐标系

闵氏时空坐标是一个复坐标系，所以其中旋转矩阵的几个三角函数值要乘一个虚数单位 \(i\) 。

由于 \(y,z\) 在变换中始终不变，就只讨论 \(ict-x\) 平面。

我们先把洛伦兹变换中的时间式换成 \(ict\) :

\[t'= \gamma(t-\frac{u}{c^2}x)\implies ict'= \gamma(ict-i\frac{u}{c}x) \]

再把洛伦兹变换的矩阵形式写出来：

\[\begin{bmatrix} x'\\ ict' \end{bmatrix} = \begin{bmatrix} \gamma & i\beta\gamma\\ -i\beta\gamma & \gamma \end{bmatrix} \begin{bmatrix} x\\ ict \end{bmatrix} \]

会发现变换矩阵形式莫名地像旋转矩阵，而且：

\[\gamma^2+(i\beta\gamma)^2=1 \]

那我们不妨来猜一猜，\(\gamma=Cos\theta\;,\;i\beta\gamma=Sin\theta\;,\;i\beta=Tan\theta\) 。

将 \(\gamma\) 中的 \(\beta\) 项换成 \(Tan\theta\) ，刚好化出来是 \(Cos\theta\) 。并且由于是在复平面上， \(Sin\theta\) 和 \(Tan\theta\) 是虚数。

那么，洛伦兹变换就相当于将闵氏时空的坐标系逆时针旋转 \(\theta\) ，其中 \(Tan\theta=i\beta\) 。

通过闵氏时空解释尺短钟慢

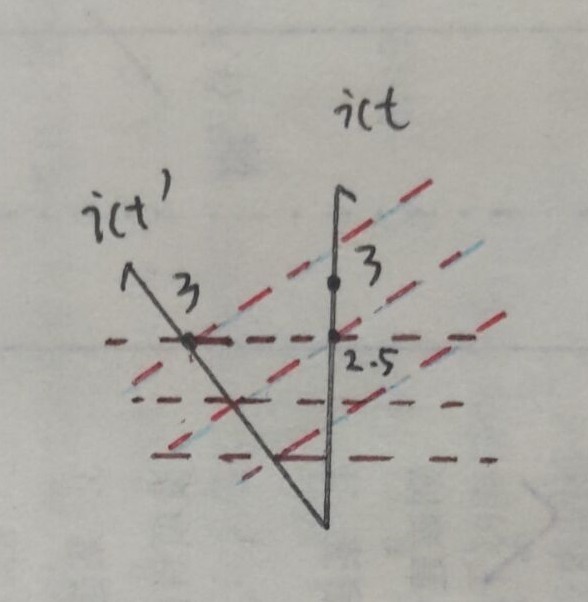
如图，\(ict'\) 坐标为 \(3\) 的位置，在 \(ict\) 中小于 \(3\) 。反过来同理，这就是为何钟慢。

尺短也可以类似解释。

闵氏空间解释双生子佯谬

终于到了解决这个疑惑的时候了。

答案是出去旅行的哥哥更年轻。

原因如图，橙色线是飞船参照系的时间轴坐标网格。

可以看见，飞离地球时，哥哥一直认为弟弟所在时间进行的慢。

而在减速回途时，由于速度改变，参照系迅速扭转，这时哥哥观测下弟弟的时间会飞速加快，超过自己的。

而在回途后，哥哥会觉得弟弟时间变慢，但是参照系扭转程度极大，所以还是弟弟时间快。

而之前我们的纠结是因为忽略了变速阶段，出现了上图左边的时间跳跃，跳过了弟弟的一段时间。

当然还有更暴力的方法，计算固有时 \(\tau=\frac{\sqrt{|x^2-c^2t^2|}}{c}\) 。

由于 \(c\) 极大，所以结果肯定为负，而哥哥有 $\Delta x $ 值，所以绝对值会小一点，固有时也小，所以哥哥年轻。

声明和感谢

本文仅代表个人意见，不保证出现错误。

参考资料：

• 分钟物理
• 耶鲁大学公开课
• tck's blog 虽然感觉有错

部分参考源自百度百科和知乎

---

-EOF-