一个思考Exlucas时的错误思路和对CRT的一些理解
\(Exlucas\) 的模板问题是求:
\[C^{n}_{m}\quad(mod\;p)
\]
其中, \(n\) , \(m\) 很大,不能够直接求阶乘。\(p\) 大小可接受但是不保证是质数。
扩展的思路是把 \(p\) 进行质因数分解,然后分别模分解后的 \(p_i^k\) 再用 \(CRT\) 组合起来。
我当时刚刚学完 \(Lucas\) 以为扩展是赤裸裸的 \(CRT+Lucas\) ,就想直接模 \(p_i\) 不行吗?
并且陷入了这样一个问题:
给定 \(x\) 满足:
\[\begin{cases}
x\equiv a_1\quad(mod\;p_1)\\
x\equiv a_2\quad(mod\;p_2)\\
\cdots\\
x\equiv a_n\quad(mod\;p_n)\\
\end{cases}
\\
\bf 和\\
\rm
\begin{cases}
x\equiv b_1\quad(mod\;p_1^{k_1})\\
x\equiv b_2\quad(mod\;p_2^{k_2})\\
\cdots\\
x\equiv b_n\quad(mod\;p_n^{k_n})\\
\end{cases}
\]
作为前提的 \(x\) 是一样的,那么 \(CRT\) 为什么解出来的不同的 \(x\) 呢。(当时我真的是蠢枯了
现在看来,显而易见,\(x\) 不是唯一的,而是以所以模数的公倍数 \(M\) 为间隔的无限个数。
我们求出来的是满足条件的最小正整数解。第一个和第二个的解的关联是这样的:
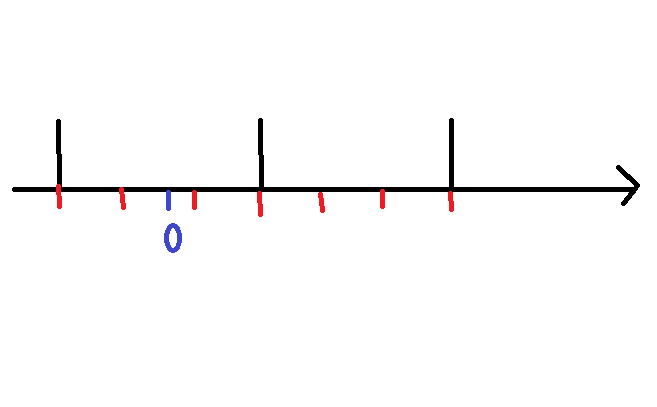
所以,我们用 \(p_i\) 那组解出来的和 \(p_i^{k_i}\) 那组解出来的不是一个,而且也没法(或者我不知道,但是既然 \(Exlucas\) 还存在,那应该是没有)用其中一个还原另外一个。
所以,必须对 \(p_i^{k_i}\) 取模,就需要 \(Exlucas\) 的那些操作了。
-EOF-

