P4168 蒲公英 题解
传送门:P4168 蒲公英
这种打法只能开O2过qaq(可能是常数太大但是我懒得改了)
本题是一道神仙分块,有一些神奇的小细节
问题的模型是给你一串序列,然后查询其中任意一段的众数。一段扫复杂度肯定不行。但是众数也不能用线段树记
。于是就有了神奇的分块。(然鹅实际上是不可能想出来的)
正文:
首先,由于颜色编号过大要离散化,这里附上两种离散化(因为本来打的 map 但是其调用自带至少 \(lg{n}\) 复杂度然后就很惨的T了)
map
void input(){
///map离散化/// o(n)
sett[0]=0;
for(int i=1;i<=n;i++){
scanf("%d",&violet[i]);
if(!ok[violet[i]]){
sett[violet[i]]=++cnt;
antiid[cnt]=violet[i];
ok[violet[i]]=true;
}
}
for(int i=1;i<=n;i++){
id[i]=sett[violet[i]];
}
}
unique
for(int i=1;i<=n;i++){
scanf("%d",&violet[i]);
lsh[i].violet=violet[i];
lsh[i].i=i;
}
sort(lsh+1,lsh+1+n,cmp1);
for(int i=1;i<=n;i++){
lsh[i].id=lsh[i-1].id;
if(lsh[i].violet!=lsh[i-1].violet){
++lsh[i].id,cnt++;
antiid[lsh[i].id]=lsh[i].violet;
}
}
sort(lsh+1,lsh+1+n,cmp2);
for(int i=1;i<=n;i++){
id[i]=lsh[i].id;
}
}
我们可以 \(\sqrt{n}\) 为一个区间,一共 \(\sqrt{n}\) 或 \(\sqrt{n}+1\) 个区间;
如下图:

分完了块,就可以进行统计众数的操作了。
首先,我们的思路是将询问区间分为连续整块和散落的点;这样询问区间的众数就只可能是整区间的众数和任意一个散点。这时我们就要比较散点中的数在区间中的个数。
这个操作有两种思路:
-
思路1:建一个 vector a[i] ,存储种类 i 的每一个出现的位置,再建一个v[ j ],储存第 j 位是此位的种类中的第几个(有点拗口,其实是前缀和);\(\quad\) 当询问时,二分求出左右边界然后将左右边界的 v 值相减求出区间中此种类的个数。
这个方法复杂度要 \(O(lg{n})\) -
思路2:预处理一个数组 \(s[ i ][ j ]\) 。代表第 j 种颜色在前 i 个块中的个数,然后如同上述分块思想,将询问区间分为散点和整块处理。然后就能 \(O(1)\) 查询辽。
值得一提的是预处理操作,初想时容易以为是 \(O(n)\) 的操作,实则不然。由于每次 \(i+1\) 时 \(s[ i ][ j ] \quad j \in [1,n]\) 中的值并未更新至 \(s[ i+1 ][ j ] \quad j \in [1,n]\) 中,所以并不能一遍扫过去,而需要逐块更新;
\(\quad\)具体操作见代码:
/// s[i][j] // 预处理第j种颜色在前i个块中的前缀和
/// o((√n)^2 + n)=o(n)
for(int i=1;i<=len;i++){
for(int j=1;j<=cnt;j++){
s[i][j]=s[i-1][j];
}
for(int j=(i-1)*T+1;j<=i*T && j<=n;j++){
s[i][id[j]]++;
}
}
然后回到处理区间众数 \(pub[ i ][ j ]\) ,预处理区间众数的思路很像查询众数,首先我们用两个for循环遍历任意的 \(i,j \quad i,j \in [1,len] ,i\leq j \quad\) (其中 len 是区间总数)。这时我们会发现,当求 \(pub[ i ][ j ]\)
时, \(pub[ i ][ j-1 ]\) 是已知的。那么我们遍历 \(j\) 区间内的每一个数,比较其在区间中的个数和现在的众数的个数就行了(这里就能用到刚才的 \(s\) 数组了)。至于题中的等量众数的优先规则,加个判定就行了。
下面贴代码:
///预处理两块之间众数
/// o((√n)^3)=o(n*√n)
for(int i=1;i<=len;i++){
for(int j=i;j<=len;j++){
int t=pub[i][j-1];
int maxn=s[j][t]-s[i-1][t];
for(int k=(i-1)*T+1;k<=j*T && k<=n;k++){
int num=s[j][id[k]]-s[i-1][id[k]];
if(num>maxn || ((num==maxn) && (violet[k] <= antiid[t]))){
t=id[k];
maxn=num;
}
}
pub[i][j]=t;
}
}
最后是查询操作:
当拿到查询区间 \([l,r]\) 首先计算区间内编号最大和最小的块,从而把查询区间分为一长串整块和若干(不超过 \(2\sqrt{n}\))散点; \(\quad\) 而对于 \(n\) 个数的序列,以 \(T= \lfloor\sqrt{n}\rfloor\) 为区间长。
这样的话,对于一个编号为 \(i\) 的所在块 $ id( i ) $ 有:
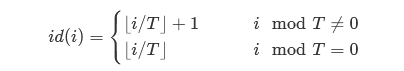
所以我们就要找 \(id(l)+1\) 和 \(id(r)-1\) 就行了
如图
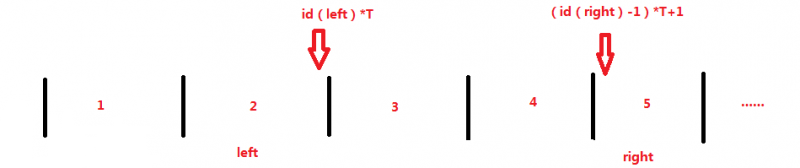
然鹅这还没完,还有两个特殊情况:
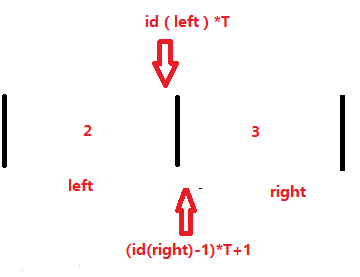
我们发现这种情况是没有整块的,但是实际操作会把 \(r\) 所在的区间众数算上;
这时我们就要手动特判一下
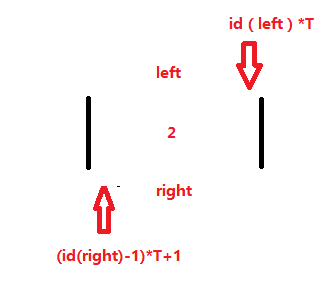
这种情况整块会统计成 0 所以并无大碍;但是散点遍历时会将整个区间统计上,同样也应特判。
最后贴上位置代码:
#include<cstdio>
#include<cstring>
#include<map>
#include<cmath>
#include<algorithm>
using namespace std;
map<int,int> sett;
map<int,bool> ok;
int id[40050],antiid[40050],vis[40050];
int n,m,cnt,tot,len,T,x;
int s[250][40050],pub[250][250],neww[500],neww_sum[40050];
int violet[40050];
void input(){
///map离散化/// o(n)
sett[0]=0;
for(int i=1;i<=n;i++){
scanf("%d",&violet[i]);
if(!ok[violet[i]]){
sett[violet[i]]=++cnt;
antiid[cnt]=violet[i];
ok[violet[i]]=true;
}
}
for(int i=1;i<=n;i++){
id[i]=sett[violet[i]];
}
}
void init_(){
scanf("%d %d",&n,&m);
///分块///
T=sqrt(n);
len=n/T;
if((n%T)!=0) len++;
input();
/// s[i][j] // 预处理第j种颜色在前i个块中的前缀和/// o(\sqrt(n)^2 + n)=o(n)
for(int i=1;i<=len;i++){
for(int j=1;j<=cnt;j++){
s[i][j]=s[i-1][j];
}
for(int j=(i-1)*T+1;j<=i*T && j<=n;j++){
s[i][id[j]]++;
}
}
///预处理两块之间众数/// o(\sqrt(n)^3)=o(n*\sqrt(n))
for(int i=1;i<=len;i++){
for(int j=i;j<=len;j++){
int t=pub[i][j-1];
int maxn=s[j][t]-s[i-1][t];
for(int k=(i-1)*T+1;k<=j*T && k<=n;k++){
int num=s[j][id[k]]-s[i-1][id[k]];
if(num>maxn || ((num==maxn) && (violet[k] <= antiid[t]))){
t=id[k];
maxn=num;
}
}
pub[i][j]=t;
}
}
}
void calc(int l,int r){
///判定左右边界和所属块
int t1=l/T+1,t2=r/T;
if(l%T == 0) t1--;
if(r%T == 0) t2--;
int l0=(t1)*T,r0=t2*T+1;
tot=0;
if(l0>r0) l0=r,r0=l;
///清零 // o(\sqrt(n))
for(int i=l;i<=l0;i++){
neww_sum[id[i]]=0,vis[id[i]]=0;
}
for(int i=r0;i<=r;i++){
neww_sum[id[i]]=0,vis[id[i]]=0;
}
//统计零散点的个数 // o(2*\sqrt(n))
for(int i=l;i<=l0;i++){
if(!vis[id[i]]){
vis[id[i]]=1;
neww[++tot]=id[i];
}
neww_sum[id[i]]++;
}
for(int i=r0;i<=r;i++){
if(!vis[id[i]]){
vis[id[i]]=1;
neww[++tot]=id[i];
}
neww_sum[id[i]]++;
}
///统计最终答案 /// o(\sqrt(n))
int t=pub[t1+1][t2];
int maxn=s[t2][t]-s[t1][t];
if(t2<=t1) maxn=0,t1=t2=0; //特判
for(int i=1;i<=tot;i++){
int num=neww_sum[neww[i]]+s[t2][neww[i]]-s[t1][neww[i]];
if(num>maxn || ((num==maxn) && (antiid[neww[i]]<=antiid[t]))){
t=neww[i];
maxn=num;
}
}
x=antiid[t];
printf("%d\n",x);
}
void work(){
int l,r;
for(int i=1;i<=m;i++){
int l0,r0;
scanf("%d %d",&l0,&r0);
l=(l0+x-1)%n+1;
r=(r0+x-1)%n+1;
if(l>r) swap(l,r);
calc(l,r);
}
}
int main()
{
//n<=40000 m<=50000
init_(); //o(n*\sqrt(n))
work(); // o(m*\sqrt(n))
return 0;
}


