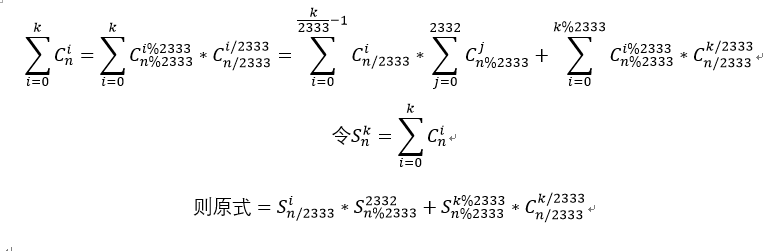loj #2038. 「SHOI2015」超能粒子炮・改

 

#2038. 「SHOI2015」超能粒子炮・改

 

题目描述

曾经发明了脑洞治疗仪与超能粒子炮的发明家 SHTSC 又公开了他的新发明：超能粒子炮・改——一种可以发射威力更加强大的粒子流的神秘装置。

超能粒子炮・改相比超能粒子炮，在威力上有了本质的提升。它有两个参数 nnn、kkk，它会向每个编号为 000 到 kkk（包含两端）的位置 iii 发射威力为 ${\mathrm{Cinmod2333 的粒子流。}}^{}$

现在 SHTSC 给出了他的超能粒子炮・改的参数，让你求出其发射的粒子流的威力之和除以 233323332333 所得的余数。

输入格式

第一行一个整数 ttt 表示数据组数。
之后 ttt 行，每行两个整数 nnn、kkk，含义如题面描述。

输出格式

ttt 行，每行一个整数，表示其粒子流的威力之和模 233323332333 的值。

样例

样例输入

3
5 5
10 7
1145 14

样例输出

32
968
763

数据范围与提示

对于 10%10\%10% 的数据，t=1t = 1t=1，n,k≤1000n, k \leq 1000n,k≤1000；
对于 30%30\%30% 的数据，t=1t = 1t=1，n,k≤1000000n, k \leq 1000000n,k≤1000000；
对于 50%50\%50% 的数据，t=1t = 1t=1，n≤1018,k≤1000n \leq 10^{18}, k \leq 1000n≤10​18​​,k≤1000；
对于 70%70\%70% 的数据，t=100t = 100t=100，n,k≤1018n, k \leq 10^{18}n,k≤10​18​​；
对于 100%100\%100% 的数据，t=100000t = 100000t=100000，n,k≤1018n, k \leq 10^{18}n,k≤10​18​​。

 

 

#include<iostream>
#include<cstdio>
#include<cstring>
#define mod 2333
#define maxn 3010
using namespace std;
int T,fac[maxn],inv[maxn];
long long n,k;
int Pow(int x,int y){
    int res=1;
    while(y){
        if(y&1)res=1LL*res*x%mod;
        x=1LL*x*x%mod;
        y>>=1;
    }
    return res;
}
long long C(long long n,long long m){
    if(m>n)return 0;
    return 1LL*fac[n]*inv[m]%mod*inv[n-m]%mod;
}
long long Lucas(long long n,long long m){
    if(m==0)return 1;
    return 1LL*C(n%mod,m%mod)*Lucas(n/mod,m/mod)%mod;
}
int main(){
    scanf("%d",&T);
    fac[0]=inv[0]=1;
    for(int i=1;i<=3000;i++){
        fac[i]=1LL*fac[i-1]*i%mod;
        inv[i]=Pow(fac[i],mod-2);
    }
    int ans;
    while(T--){
        ans=0;
        cin>>n>>k;
        for(int i=0;i<=k;i++){
            ans+=Lucas(n,i);
            if(ans>=mod)ans-=mod;
        }
        printf("%d\n",ans);
    }
    return 0;
}

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int mod=2333;
long long sum[2335][2335];
long long Pow(long long x,long long k){
    int res=1;
    while(k){
        if(k&1)res=res*x%mod;
        x=x*x%mod;
        k>>=1;
    }
    return res;
}
long long fact[mod+10],inv[mod+10];
void init(){
    fact[0]=1;
    inv[0]=1;
    for(int i=1;i<=mod;i++){
        fact[i]=fact[i-1]*i%mod;
        inv[i]=Pow(fact[i],mod-2);
    }
}
long long Lucas(long long n,long long m){
    long long a,b,res=1LL;
    while(n&&m){
        a=n%mod,b=m%mod;
        if(a<b)return 0LL;
        res=res*fact[a]%mod*inv[b]%mod*inv[a-b]%mod;
        n/=mod,m/=mod;
    }
    return res;
}
long long cal(long long n,long long k){
    if(k<mod&&n<mod)
        return sum[n][k];
    long long ans=0;
    ans+=Lucas(n/mod,k/mod)*sum[n%mod][k%mod]%mod;
    ans%=mod;
    if(k>=mod)
        ans+=cal(n/mod,k/mod-1)*sum[n%mod][mod-1]%mod;
    ans%=mod;
    return ans;
}
int main(){
    int T;
    init();
    for(int i=0;i<mod;i++){
        for(int j=0;j<=i;j++){
            sum[i][j]=Lucas(i,j);
        }
        for(int j=1;j<mod;j++){
            sum[i][j]+=sum[i][j-1];
            sum[i][j]%=mod;
        }
    }
    scanf("%d",&T);
    while(T--){
        long long k,n;
        scanf("%lld%lld",&n,&k);
        printf("%lld\n",cal(n,k));
    }
    return 0;
}