洛谷P1930 亚瑟王的宫殿 Camelot
题目描述
很久以前,亚瑟王和他的骑士习惯每年元旦去庆祝他们的友谊。为了纪念上述事件, 我们把这些故事看作是一个棋盘游戏。有一个国王和若干个骑士被放置在一个由许多方格 组成的棋盘上,没有两个骑士在同一个方格内。
这个例子是标准的 8*8 棋盘
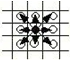
国王可以移动到任何一个相邻的方格,从下图中黑子位置到下图中白子位置前提是他 不掉出棋盘之外。
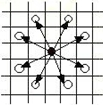
一个骑士可以从下图中黑子位置移动到下图中白子位置(走“日”字形) 但前提是他 不掉出棋盘之外。
在游戏中,玩家可在每个方格上放不止一个棋子,假定方格足够大,任何棋子都不会 阻碍到其他棋子正常行动。
玩家的任务就是把所有的棋子移动到同一个方格里——用最小的步数。为了完成这个 任务,他必须按照上面所说的规则去移动棋子。另外,玩家可以选择一个骑士跟国王从他 们两个相遇的那个点开始一起行动,这时他们按照骑士的行动规则行动,其他的单独骑士 则自己一直走到集中点。骑士和国王一起走的时候,只算一个人走的步数。
请计算他们集中在一起的最小步数,而且玩家必须自己找出这个集中点。当然,这些 棋子可以在棋盘的任何地方集合。
输入输出格式
输入格式:
第一行: 两个用空格隔开的整数:R,C 分别为棋盘行和列的长。不超过 26 列,40 行。
第二行到结尾: 输入文件包含了一些有空格隔开的字母/数字对,一行有一个或以 上。第一对为国王的位置,接下来是骑士的位置。可能没有骑士,也可能整个棋盘都是骑 士。行从 1 开始,列从大写字母 A 开始。
输出格式:
单独一行表示棋子集中在一个方格的最小步数。
输入输出样例
说明
【样例说明】
他们集中在 B5。
骑士 1: A3 - B5 (1 步)
骑士 2: A8 - C7 - B5 (2 步)
骑士 3: H1 - G3 - F5 - D4 (此时国王开始与这个骑士一起走) - B5 (4 步) 骑士 4: H8 - F7 - D6 - B5 (3 步)
1 + 2 + 4 + 3 = 10 步
题目翻译来自NOCOW。
USACO Training Section 3.3
/* 宽搜 */ #include<iostream> #include<cstdio> #include<cstring> #include<vector> #include<queue> #define maxn 50 using namespace std; int n,m,f[maxn][maxn],kx,ky,ans=1<<29,stp[maxn][maxn]; bool p[maxn][maxn]; int e[8][2]={{1,2},{2,1},{-1,2},{2,-1},{1,-2},{-2,1},{-2,-1},{-1,-2}}; int ke[8][2]={{1,0},{0,1},{-1,0},{0,-1}}; struct node{int x,y;}; char c[5]; queue<node>q; vector<node>K; node make_node(int x,int y){ node res;res.x=x;res.y=y; return res; } bool Judge(int x,int y){ if(x<1||y<1||x>n||y>m)return 0; if(f[x][y]!=-1)return 0; return 1; } bool judge(int x,int y){ if(x<1||y<1||x>n||y>m)return 0; if(p[x][y])return 0; return 1; } bool pd(int x,int y){ if(x<1||y<1||x>n||y>m)return 0; if(stp[x][y]!=-1)return 0; return 1; } int calc_king(){ int rec=(1<<29); int u,v,x=kx,y=ky; memset(stp,-1,sizeof(stp)); while(!q.empty())q.pop(); q.push(make_node(x,y)); stp[x][y]=0; while(!q.empty()){ x=q.front().x,y=q.front().y;q.pop(); if(p[x][y])rec=min(rec,stp[x][y]); for(int i=0;i<8;i++){ u=x+e[i][0];v=y+e[i][1]; if(!pd(u,v))continue; stp[u][v]=stp[x][y]+1; if(p[u][v])rec=min(rec,stp[u][v]); else q.push(make_node(u,v)); } } return rec; } void Jump(int x,int y){ p[x][y]=1; int u,v,xx,yy; for(int i=0;i<=8;i++){ u=x+e[i][0];v=y+e[i][1]; if(!judge(u,v))continue; if(f[u][v]+1==f[x][y])Jump(u,v); } } int bfs(int x,int y){ int rec=0,u,v; while(!q.empty())q.pop(); q.push(make_node(x,y)); f[x][y]=0; memset(p,0,sizeof(p)); p[x][y]=1; while(!q.empty()){ x=q.front().x;y=q.front().y;q.pop(); for(int i=0;i<8;i++){ u=x+e[i][0],v=y+e[i][1]; if(!Judge(u,v))continue; f[u][v]=f[x][y]+1; q.push(make_node(u,v)); } } for(int i=0;i<K.size();i++){ x=K[i].x,y=K[i].y; if(f[x][y]<0)return (1<<29); rec+=f[x][y]; if(rec>=ans)return rec; Jump(x,y); } rec+=calc_king(); return rec; } int main(){ freopen("Cola.txt","r",stdin); int k; scanf("%d%d",&n,&m); scanf("%s%d",c,&k); ky=c[0]-'A'+1;kx=k; while(scanf("%s%d",c,&k)!=EOF) K.push_back(make_node(k,c[0]-'A'+1)); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ memset(f,-1,sizeof(f)); ans=min(ans,bfs(i,j)); } printf("%d\n",ans); return 0; }
