2017-10-5 清北刷题冲刺班a.m
行列式

序列

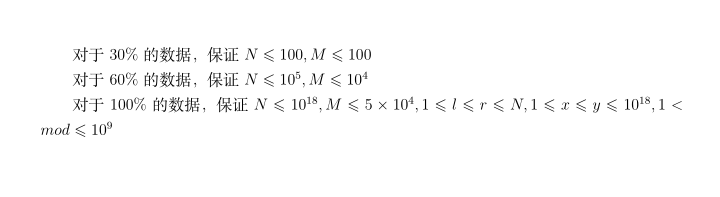

#include<iostream> #include<cstdio> #define maxn 500010 using namespace std; int n,m,mod,l,r,x,y,b[maxn],a[maxn],cnt; void dfs(int now[],int sz){ if(sz<=2){ for(int i=1;i<=sz;i++)b[++cnt]=now[i]; return; } int sz1=0,sz2=0; int d[sz],c[sz]; for(int i=1;i<=sz;i++){ if(i%2!=0){//奇数位 c[++sz1]=now[i]; } if(i%2==0){//偶数位 d[++sz2]=now[i]; } } dfs(c,sz1); dfs(d,sz2); } int main(){ //freopen("Cola.txt","r",stdin); freopen("seq.in","r",stdin);freopen("seq.out","w",stdout); scanf("%d%d%d",&n,&m,&mod); for(int i=1;i<=n;i++)a[i]=i; dfs(a,n); long long ans; for(int i=1;i<=m;i++){ scanf("%d%d%d%d",&l,&r,&x,&y); ans=0; if(x>y)swap(x,y); for(int j=l;j<=r;j++){ if(b[j]<=y&&b[j]>=x){ ans=(ans+b[j])%mod; } }printf("%I64d\n",ans); } fclose(stdin);fclose(stdout); return 0; }

/* 考虑类似线段树的求解方法,记 getans(n,l,r,x,y) 表示当前在 F 中,是 1 到 n 的升序 排列,需要求得最终排好序后 l 到 r 范围内,大小在 x 到 y 之间的数值之和以及数字个数 (getans 返回一个 pair) ,思考如何分治。 注意到左右分裂的规律,可以算出此时序列需要向左边和右边分出多少,同时可以知道 l,r,x,y 四个数在子区间的大小,分治下去求解。在回溯时,将左右子树答案合并即可。 注意如果实现过程中会有类平方运算,可能会超 Long Long 范围,需要特别注意处理。 具体实现详见代码,复杂度为 O(M logN)。 */ #include<iostream> #include<cstdio> #include<cstring> #ifdef WIN32 #define LL "%I64d" #else #define LL "%lld" #endif using namespace std; struct node{ long long a,b; }; long long n,m,mod,l,r,u,v; node make_node(long long x,long long y){ node w; w.a=x;w.b=y; return w; } node solve(long long rr,long long l,long long r,long long x,long long y){ if(x>rr||l>r)return make_node(0,0); if(l==1&&r==rr){ x=max(x,1LL); y=min(y,rr); long long s; if((x+y)%2==0)s=((x+y)/2)%mod*((y-x+1)%mod)%mod; else s=((x+y)%mod)*((y-x+1)/2%mod)%mod; return make_node(s%mod,y-x+1); } long long mid=(rr+1)/2; if(r<=mid){ node res=solve(mid,l,r,x/2+1,(y+1)/2); return make_node((res.a*2-res.b)%mod,res.b); } else if(l>mid){ node res=solve(rr-mid,l-mid,r-mid,(x+1)/2,y/2); return make_node(res.a*2%mod,res.b); } else{ node res1=solve(mid,l,mid,x/2+1,(y+1)/2); node res2=solve(rr-mid,1,r-mid,(x+1)/2,y/2); return make_node((res1.a*2-res1.b+res2.a*2)%mod,(res1.b+res2.b)%mod); } } int main(){ freopen("seq.in","r",stdin);freopen("seq.out","w",stdout); //freopen("Cola.txt","r",stdin); scanf(LL LL LL,&n,&m,&mod); for(int i=0;i<m;i++){ scanf(LL LL LL LL,&l,&r,&u,&v); node ans=solve(n,l,r,u,v); printf(LL"\n",(ans.a+mod)%mod); } return 0; }
数数(倍增)

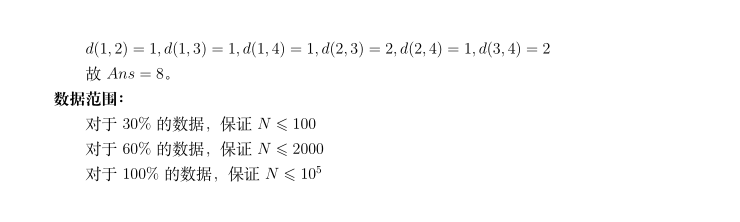

#include<iostream> #include<cstdio> #include<queue> #include<cstring> #define maxn 100010 using namespace std; int num,head[maxn]; int sz[maxn],son[maxn],fa[maxn],top[maxn],dep[maxn]; long long ans; struct node{ int to,pre; }e[maxn*2]; int n,dis[2010][2010]; bool vis[maxn]; void Insert(int from,int to){ e[++num].to=to; e[num].pre=head[from]; head[from]=num; } void Bfs(int s){ queue<int>q; memset(vis,0,sizeof(vis)); vis[s]=1;q.push(s);dis[s][s]=0; while(!q.empty()){ int now=q.front();q.pop(); for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(vis[to])continue; else { dis[s][to]=dis[s][now]+1; vis[to]=1; q.push(to); } } } } int count(int x){ int res=0; while(x){ res+=x&1; x>>=1; } return res; } void dfs1(int now,int father){ dep[now]=dep[father]+1; sz[now]=1;fa[now]=father; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(to==father)continue; dfs1(to,now); sz[now]+=sz[to]; if(!son[now]||sz[son[now]]<sz[to])son[now]=to; } } void dfs2(int now,int father){ top[now]=father; if(son[now])dfs2(son[now],father); for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(to==fa[now]||to==son[now])continue; dfs2(to,to); } } int LCA(int a,int b){ while(top[a]!=top[b]){ if(dep[top[a]]<dep[top[b]])swap(a,b); a=fa[top[a]]; } if(dep[a]>dep[b])swap(a,b); return a; } int main(){ //freopen("Cola.txt","r",stdin); freopen("bitcount.in","r",stdin);freopen("bitcount.out","w",stdout); scanf("%d",&n); int x,y; for(int i=1;i<n;i++){ scanf("%d%d",&x,&y); Insert(x,y);Insert(y,x); } for(int i=1;i<=n;i++)Bfs(i); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dis[i][j]=count(dis[i][j]); dfs1(1,0); dfs2(1,1); for(int i=1;i<=n;i++){ for(int j=i+1;j<=n;j++){ int lca=LCA(i,j); ans+=dis[i][lca]+dis[j][lca]; } } cout<<ans; fclose(stdin);fclose(stdout); return 0; }

/* 记 l(i,j) 表示 i 号节点向上 2^j 步的祖先节点。 记 f(i,j) 表示到 i 号节点,上一步长为 2^j 的数位之和。 记 g(i,j) 表示到 i 号节点,上一步长为 2^j 的方案数。 考虑转移方程: g(i,j) → g(l(i,k),k),k < j f(i,j) + g(i,j) → f(l(i,k),k),k < j 由于难以查询某一节点子树中深度为 d 的节点,该方程用自下而上更新的方法比较方便。 而 Ans 也很难用一个简洁的式子表示出,故在模拟向上跳跃的时候同步更新。 具体细节详见代码,复杂度 O(N log^2 N)。 */ #include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <string> #include <cmath> #include <vector> #define st first #define nd second using namespace std; struct edge { int x; int nxt; }; typedef long long LL; const int N = 1E5 + 10; edge e[2 * N]; int lca[N][17], hd[N], fa[N], sons[N], nxt[N], cnt[N][17], f[N][17]; int n, m, x, y, l; LL ans; void link(int x, int y) { e[++l].x = y; e[l].nxt = hd[x]; hd[x] = l; } void dfs_lca(int x) { lca[x][0] = fa[x]; sons[x] = 1; for (int i = 1; i <= 16; ++i) lca[x][i] = lca[lca[x][i - 1]][i - 1]; for (int p = hd[x]; p; p = e[p].nxt) if (e[p].x != fa[x]) { fa[e[p].x] = x; dfs_lca(e[p].x); sons[x] += sons[e[p].x]; } } void dfs_ans(int x) { for (int p = hd[x]; p; p = e[p].nxt) if (e[p].x != fa[x]) nxt[x] = e[p].x, dfs_ans(e[p].x); for (int i = 0; i <= 16; ++i) { ans += sons[lca[x][i]] - sons[nxt[lca[x][i]]]; cnt[lca[x][i]][i]++; f[lca[x][i]][i]++; } for (int i = 1; i <= 16; ++i) for (int j = 0; j <= i - 1; ++j) { ans += LL(cnt[x][i] + f[x][i]) * LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]); cnt[lca[x][j]][j] += cnt[x][i]; f[lca[x][j]][j] += f[x][i] + cnt[x][i]; } } int main() { freopen("bitcount.in", "r", stdin); freopen("bitcount.out", "w", stdout); scanf("%d", &n); for (int i = 1; i < n; ++i) { scanf("%d%d", &x, &y); link(x, y); link(y, x); } dfs_lca(1); sons[0] = sons[1]; nxt[0] = 1; dfs_ans(1); printf("%I64d\n", ans); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号