洛谷P2680 运输计划

P2680 运输计划

题目背景

公元 2044 年,人类进入了宇宙纪元。

题目描述

L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物

流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道 是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之 间不会产生任何干扰。

为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的 物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段 性工作所需要的最短时间是多少?

输入输出格式

输入格式：

 

输入文件名为 transport.in。

第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。

接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第

i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。

接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个 运输计划是从 uj 号星球飞往 vj 号星球。

 

输出格式：

 

输出 共1行,包含1个整数,表示小P的物流公司完成阶段性工作所需要的最短时间。

 

输入输出样例

输入样例#1：

6 3 
1 2 3 
1 6 4 
3 1 7 
4 3 6 
3 5 5 
3 6 
2 5 
4 5

输出样例#1：

11

说明

所有测试数据的范围和特点如下表所示

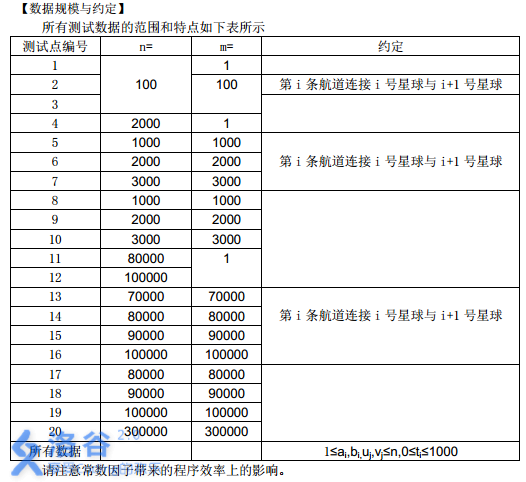
请注意常数因子带来的程序效率上的影响。

 

/*
    先LCA一遍，记下每个任务的起点，终点，公共祖先，所需时间
    然后二分答案，统计不满足答案的任务tot，然后维护一个sum[i]，
    对于每个不满足条件的任务，sum[起点]++，sum[终点]++，sum[公共祖先]-=2，
    并将它们的sum值传到父亲结点，最后看是否能找出某个点i，使sum[i]=tot并且
    连到这个点的边权值>= 最大任务时间-答案，如果能，这个答案即为可行答案。 
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 300010

using namespace std;
int n,m,num,head[maxn],edge[maxn];
int dis[maxn],Inf,sum[maxn];
int son[maxn],fa[maxn],dep[maxn],sz[maxn],top[maxn];

struct node{int to,pre,v;}e[maxn*2];
struct Node{int a1,b1,dist,anc;}lca[maxn];

void Insert(int from,int to,int v){
    e[++num].to=to;
    e[num].v=v;
    e[num].pre=head[from];
    head[from]=num;
}

void dfs1(int now,int father){
    dep[now]=dep[father]+1;
    fa[now]=father;
    sz[now]=1;
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==father)continue;
        edge[to]=i;dis[to]=dis[now]+e[i].v;
        dfs1(to,now);
        sz[now]+=sz[to];
        if(!son[now]||sz[son[now]]<sz[to])son[now]=to;
    }
}

void dfs2(int now,int father){
    top[now]=father;
    if(son[now])dfs2(son[now],father);
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==son[now]||to==fa[now])continue;
        dfs2(to,to);
    }
}

int LCA(int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    return x;
}

void dfs3(int now,int father){
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==father)continue;
        dfs3(to,now);
        sum[now]+=sum[to];
    }
}

bool check(int x){
    memset(sum,0,sizeof(sum));
    int p=0,tot=0;
    for(int i=1;i<=m;i++){
        if(lca[i].dist>x){
            tot++;
            sum[lca[i].a1]++;
            sum[lca[i].b1]++;
            sum[lca[i].anc]-=2;
            p=max(p,lca[i].dist-x);
        }
    }
    dfs3(1,1);
    for(int i=1;i<=n;i++)
        if(sum[i]==tot&&e[edge[i]].v>=p)return 1;
    return 0;
}

int main(){
    //freopen("Cola.txt","r",stdin);
    scanf("%d%d",&n,&m);
    int x,y,z;
    for(int i=1;i<n;i++){
        scanf("%d%d%d",&x,&y,&z);
        Insert(x,y,z);Insert(y,x,z);
    }
    dfs1(1,0);dfs2(1,1);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&lca[i].a1,&lca[i].b1);
        lca[i].anc=LCA(lca[i].a1,lca[i].b1);
        lca[i].dist=dis[lca[i].a1]+dis[lca[i].b1]-2*dis[lca[i].anc];
        Inf=max(Inf,lca[i].dist);
    }
    int l=0,r=Inf,ans=0;
    while(l<=r){
        int mid=(l+r)>>1;
        if(check(mid)){
            ans=mid;
            r=mid-1;
        }
        else l=mid+1;
    }
    printf("%d",ans);
}