洛谷P3807 【模板】卢卡斯定理

P3807 【模板】卢卡斯定理

题目背景

这是一道模板题。

题目描述

给定n,m,p(1\le n,m,p\le 10^51≤n,m,p≤10​5​​)

求 C_{n+m}^{m}\ mod\ pC​n+m​m​​ mod p

保证P为prime

C表示组合数。

一个测试点内包含多组数据。

输入输出格式

输入格式：

 

第一行一个整数T(T\le 10T≤10)，表示数据组数

第二行开始共T行，每行三个数n m p，意义如上

 

输出格式：

 

共T行，每行一个整数表示答案。

 

输入输出样例

输入样例#1：

2
1 2 5
2 1 5

输出样例#1：

3
3

Lucas定理是用于处理组合数取模的定理

通常用于解决阶乘无法解决的问题。

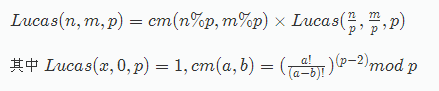
#include<bits/stdc++.h>
#define N 100010
using namespace std;
typedef long long ll;
ll a[N];
int p;
ll pow(ll y,int z,int p){
    ll res=1;y%=p;
    while(z){
        if(z&1)res=res*y%p;
        y=y*y%p;
        z>>=1;
    }
    return res;
}
ll C(ll n,ll m){
    if(m>n)return 0;
    return ((a[n]*pow(a[m],p-2,p))%p*pow(a[n-m],p-2,p)%p);
}
ll Lucas(ll n,ll m){
    if(!m)return 1;
    return C(n%p,m%p)*Lucas(n/p,m/p)%p;
}
int main(){
    int T;scanf("%d",&T);
    int n,m;
    while(T--){
        scanf("%d%d%d",&n,&m,&p);
        a[0]=1;
        for(int i=1;i<=p;i++)a[i]=(a[i-1]*i)%p;
        cout<<Lucas(n+m,n)<<endl;
    }
}