网络流
一、最大流
1.网络流是带反悔的贪心,先求出一个当前的可行流,再寻找增广路进行增广(其实就是再找新的路多输出一点流量)。为了实现网络流的增广,需要给每条边都建一个反向边,有大小为delta的流进入这条边时,这条边的容量-delta,其反向边的容量+delta。
这样做的原理是斜对称性。x向y流了flow的流量,就相当于y向x流了-flow的流量,两者是等价的,因此可以建反向边来支持往返流动,达到增广的目的。
举个例子,下面的网络中,容量为0的边为反向边
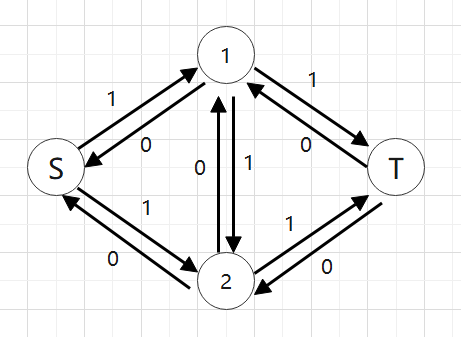
在红色路径注入1单位水,那么这些边的容量都减去1,其反向边容量都加1

很显然这个流不是最大流,如果没有反向边的话就无路可走,现在来看,中间的反向边可以向上流过1单位流量,这样就出现了一条增广路(蓝色的部分)

现在从S到T已经不相通了,那么最大流就是2,做到这里会发现,节点1和2之间实际上根本没有水流,而我们第一条可行流走的是S-1-2-T,也就是说后来1-2这条路上反悔了,这就是网络流的精髓。
但是不必纠结水流到底是怎么流的,比如有人看到这里就会想,这不就是S-1-T和S-2-T吗,并不是,实际流的是S-1-2-T和S-2-1-T,两个有什么不同呢,前者的思路是一次性流过了两个流,后者的思路是先走了第一个流,再走的第二个流,但两个流法的效果是一样的。前面那种流法看起来更简单,实际上很难实现,怎么保证这个流一定不会走1-2呢,不大好解决,我猜正因为这个,才有人想出分步灌流量,给出反悔的余地。
2.dinic算法
dinic算法是EK的优化,所以一般来说掌握了dinic就可以,下面说一下dinic的算法步骤:
(1)利用bfs对原来的图进行分层,标记每个点的层次,这个标记的含义是当前节点距离源点的最短距离。(构建层次图时所走的边的残余流量必须大于0)
(2)用dfs寻找从源点到汇点的通路(增广路),每条增广路要保证层次递增。
(3)重复步骤2,找不到增广路的时候,将新增流量加入答案,然后重复步骤1,重新建立层次图,直到从源点不能到达汇点为止。

/* 一定要建边权为0的反向边 别忘了dinic的三个优化: 1、当前弧优化,访问这个点的出边时,从上一次访问的下一条边开始 2、当增广到某个点时,增广过程中,已出去的流量==进来的,停止增广;增广完毕时,出去的流量<进来的流量,标记这个点,以后不再访问此点 3、分层时,找到汇点后即刻return,不要等到队列为空 */ #include<iostream> #include<cstdio> #include<queue> #define maxn 10010 using namespace std; int n,m,ans,head[maxn],cur[maxn],f[maxn],lev[maxn],num=1,s,t; struct node{ int to,pre,cap; }e[100010*2]; void Insert(int from,int to,int v){ e[++num].to=to; e[num].cap=v; e[num].pre=head[from]; head[from]=num; } bool bfs(int st){ queue<int>q; q.push(st); for(int i=1;i<=n;i++)cur[i]=head[i],lev[i]=-1; lev[st]=0; while(!q.empty()){ int now=q.front();q.pop(); for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(lev[to]==-1&&e[i].cap>0){ lev[to]=lev[now]+1; q.push(to); if(to==t)return 1; } } } return 0; } int dinic(int now,int flow){ if(now==t)return flow; int rest=0,delta; for(int &i=cur[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].cap>0&&lev[to]==lev[now]+1){ delta=dinic(to,min(flow-rest,e[i].cap)); if(delta){ e[i].cap-=delta;e[i^1].cap+=delta; rest+=delta;if(rest==flow)break; } } } if(rest!=flow)lev[now]=-1; return rest; } int main(){ scanf("%d%d%d%d",&n,&m,&s,&t); int x,y,z; for(int i=1;i<=m;i++){ scanf("%d%d%d",&x,&y,&z); Insert(x,y,z);Insert(y,x,0); } while(bfs(s)) ans+=dinic(s,0x7fffffff); printf("%d",ans); }
2018 ACM/ICPC 南京 I题 Magic Potion(最大流)
题意:有n个英雄,m个怪物,每个英雄有一个可打的怪物集合,一个英雄只能打一个怪物。有k瓶魔法药水,一个英雄最多喝一瓶魔法药水,喝完之后可以多打一个怪物。问最多有几个怪物会被打死。
解:英雄和怪物之间的连线不必多说,主要是起点的设置。设了三个S,S是最终的起点,S1表示正常打怪的起点,S2表示喝药水的额外打怪起点,很显然,S应该向S1和S2分别建权值为n和k的边,S1和S2都向每个英雄建权值为1的边,效果如下图:


#include<iostream> #include<cstdio> #include<cstring> #include<queue> #define maxn 510*3 #define maxm 300010 using namespace std; int n,m,k,S,S1,S2,T; int num=1,head[maxn],cur[maxn],lev[maxn]; struct node{ int to,pre,cap; }e[maxm*2]; void Insert(int from,int to,int v){ e[++num].to=to; e[num].cap=v; e[num].pre=head[from]; head[from]=num; } bool bfs(int s){ queue<int>q; for(int i=1;i<=n+m+4;i++)cur[i]=head[i],lev[i]=-1; lev[s]=0;q.push(s); while(!q.empty()){ int now=q.front();q.pop(); for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(lev[to]==-1&&e[i].cap>0){ q.push(to); lev[to]=lev[now]+1; // if(to==T)return 1; } } } if(lev[T]>=0)return 1; return 0; } int dinic(int now,int flow){ int rest=0; if(now==T)return flow; for(int &i=cur[now];i;i=e[i].pre){ int to=e[i].to; if(lev[to]>lev[now]&&e[i].cap>0){ int delta=dinic(to,min(e[i].cap,flow-rest)); if(delta){ rest+=delta; e[i].cap-=delta; e[i^1].cap+=delta; if(rest==flow)break; } } } if(rest<flow)lev[now]=-1; return rest; } int main(){ scanf("%d%d%d",&n,&m,&k); S=1;S1=2;S2=3;T=3+n+m+1; Insert(S,S1,n);Insert(S1,S,0); Insert(S,S2,k);Insert(S2,S,0); int x,y; for(int i=1;i<=n;i++){ Insert(S1,3+i,1);Insert(3+i,S1,0); Insert(S2,3+i,1);Insert(3+i,S2,0); scanf("%d",&x); for(int j=1;j<=x;j++){ scanf("%d",&y); Insert(3+i,3+n+y,1); Insert(3+n+y,3+i,0); } } for(int i=n+4;i<=n+m+3;i++){ Insert(i,T,1); Insert(T,i,0); } int ans=0; while(bfs(S)) ans+=dinic(S,0x7fffffff); printf("%d\n",ans); }
二、最小割
最小割=最大流
一个割表示将这些边割掉之后,S与T不再连通。首先要说的是,网络中的任何一个一个割一定大于等于任何一个流,可以理解为在割掉这些边之后,所有原本应该向后流的水,全都流失了,这些流失的水(V)一定小于等于割掉边的容量和(Cap),大于等于最大流(maxFlow)(因为后面的边仍然会约束流量),也就是$Cap\geq V \geq maxFlow$,则有$Cap\geq maxFlow$。
所以最小的割就是使割掉的边的流量完全等于流过的水流,比如有一条水流的路径为1-2-3-4,那么这个水流的大小一定是1-2,2-3,3-4这三条路径中最细的一条,如果3-4最细,就割3-4,将水从3这个口子放走,那么这条通道的水流就全部流失了。这样以此类推,就可以得出结论:最小割=最大流。
三、最小费用最大流
与最大流相似,将bfs改成spfa,原来的lev数组用dis数组替代

#include<iostream> #include<cstdio> #include<queue> #include<cstring> #define INF 1e9 #define maxn 200010 using namespace std; int n,m,s,t,dis[maxn],head[maxn],num=1,ans; bool vis[maxn]; struct node{ int to,pre,c,cc; }e[maxn]; void Insert(int from,int to,int c,int cc){ e[++num].to=to; e[num].c=c; e[num].cc=cc; e[num].pre=head[from]; head[from]=num; } bool spfa(){ deque<int>q;q.push_front(s); memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++)dis[i]=INF; dis[s]=0;vis[s]=1; while(!q.empty()){ int now=q.front(); q.pop_front(); vis[now]=0; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].c>0&&dis[to]>dis[now]+e[i].cc){ dis[to]=dis[now]+e[i].cc; if(!vis[to]){ if(!q.empty()&&dis[to]<dis[q.front()])q.push_front(to); else q.push_back(to); } } } } return dis[t]<INF; } int dfs(int x,int flow){ if(x==t){vis[t]=1;return flow;} int delta,rest=0; vis[x]=1; for(int i=head[x];i;i=e[i].pre){ int to=e[i].to; if(e[i].c>0&&!vis[to]&&dis[to]==dis[x]+e[i].cc){ delta=dfs(to,min(e[i].c,flow-rest)); if(delta){ e[i].c-=delta;e[i^1].c+=delta; rest+=delta;ans+=e[i].cc*delta; if(rest==flow)break; } } } return rest; } int costflow(){ int flow=0; while(spfa()){ vis[t]=1; while(vis[t]){ memset(vis,0,sizeof(vis)); flow+=dfs(s,INF); } } return flow; } int main(){ scanf("%d%d%d%d",&n,&m,&s,&t); int x,y,c,cc; for(int i=1;i<=m;i++){ scanf("%d%d%d%d",&x,&y,&c,&cc); Insert(x,y,c,cc); Insert(y,x,0,-cc); } printf("%d ",costflow());//最大流的大小 printf("%d",ans);//最小费用 }
poj 2135 Farm Tour
题意:有n个点,m条无向边,求从1到n再回到1的一条最短路径,路径不能有重边。
解:如果从1到n找一条最短路,然后删掉再找一条的话,答案不会最优。可以用最小费用最大流,新建s,t节点,输入和输出流量为2。由于题目要求是无向边,那每条边新建4个边就可以了

#include<iostream> #include<cstdio> #include<cstring> #include<queue> #define maxn 10010 #define INF 1e9 using namespace std; int n,m,s,t,dis[maxn],head[maxn],num=1; long long ans; bool vis[maxn]; struct node{ int to,pre,c,cc; }e[500010]; void Insert(int from,int to,int c,int cc){ e[++num].to=to; e[num].pre=head[from]; head[from]=num; e[num].c=c; e[num].cc=cc; } bool spfa(){ for(int i=s;i<=t;i++)dis[i]=INF; memset(vis,0,sizeof(vis)); deque<int>q; vis[s]=1;q.push_front(s);dis[s]=0; while(!q.empty()){ int now=q.front(); q.pop_front(); vis[now]=0; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].c>0&&dis[to]>dis[now]+e[i].cc){ dis[to]=dis[now]+e[i].cc; if(!vis[to]){ if(!q.empty()&&dis[to]<dis[q.front()])q.push_front(to); else q.push_back(to); } } } } return dis[t]<INF; } int dfs(int now,int flow){ if(now==t){vis[t]=1;return flow;} int delta=0,rest=0; vis[now]=1; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].c>0&&!vis[to]&&dis[to]==dis[now]+e[i].cc){ delta=dfs(to,min(flow-rest,e[i].c)); if(delta){ e[i].c-=delta; e[i^1].c+=delta; ans+=delta*e[i].cc; rest+=delta; if(rest==flow)break; } } } return rest; } void costflow(){ while(spfa()){ vis[t]=1; while(vis[t]){ memset(vis,0,sizeof(vis)); dfs(s,INF); } } } int main(){ scanf("%d%d",&n,&m); int x,y,z; s=1,t=n+2; Insert(s,2,2,0);Insert(2,s,0,0); Insert(n+1,t,2,0);Insert(t,n+1,0,0); for(int i=1;i<=m;i++){ scanf("%d%d%d",&x,&y,&z); x++;y++; Insert(x,y,1,z); Insert(y,x,0,-z); Insert(y,x,1,z); Insert(x,y,0,-z); } costflow(); printf("%lld\n",ans); return 0; }
poj 3686 The Windy's
题意:需要制作n种玩具,一共有m个工厂,第i个玩具在第j个工厂制作的时间为Wij,如果一个工厂玩具没有做完,那么下一个要在这个工厂制作的玩具需要排队等候。求每个玩具制作时间的平均值。
解:如果只有一个工厂,那么总时间为T = t1 + (t1+t2) + (t1+t2+t3) + ... ... + (t1+t2+...+tn) = n*t1 + (n-1)*t2 + ... ...+ tn,这样就可以贪心的将所需时间少的安排到前面。对于m个工厂的情况,显然不能这样贪心,但是可以根据上面式子的灵感,将每个工厂拆成n个点,对于任意一个工厂的第i个点,表示在这个工厂的第倒数第i个订单,则一个玩具j如果连向这个订单,费用就为i*tj,这样就可以不受其它订单的影响了,跑一遍最小费用最大流即可。

#include<iostream> #include<cstdio> #include<cstring> #include<queue> #define maxn 200010 #define INF 1e9 using namespace std; int n,m,s,t,dis[maxn],ans,head[maxn],num=1; bool vis[maxn]; struct node{ int to,pre,c,cc; }e[10000010]; void Insert(int from,int to,int c,int cc){ e[++num].to=to; e[num].pre=head[from]; head[from]=num; e[num].c=c; e[num].cc=cc; } bool spfa(){ deque<int>q;q.push_front(s); memset(vis,0,sizeof(vis)); vis[s]=1; for(int i=s;i<=t;i++)dis[i]=INF; dis[s]=0; while(!q.empty()){ int now=q.front();q.pop_front(); vis[now]=0; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].c>0&&dis[to]>dis[now]+e[i].cc){ dis[to]=dis[now]+e[i].cc; if(!vis[to]){ vis[to]=1; if(!q.empty()&&dis[to]<dis[q.front()])q.push_front(to); else q.push_back(to); } } } } return dis[t]<INF; } int dfs(int now,int flow){ int rest=0,delta=0; if(now==t){vis[t]=1;return flow;} vis[now]=1; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].c>0&&!vis[to]&&dis[to]==dis[now]+e[i].cc){ delta=dfs(to,min(flow-rest,e[i].c)); if(delta>0){ rest+=delta; e[i].c-=delta; e[i^1].c+=delta; ans+=e[i].cc*delta; if(rest==flow)break; } } } return rest; } void costflow(){ while(spfa()){ vis[t]=1; while(vis[t]){ memset(vis,0,sizeof(vis)); dfs(s,INF); } } } void init(){ memset(head,0,sizeof(head)); num=1; } int main(){ int T,x; scanf("%d",&T); while(T--){ init(); scanf("%d%d",&n,&m); s=1;t=m*n+n+2;ans=0; for(int i=2;i<=n+1;i++){//枚举每个玩具 Insert(s,i,1,0);Insert(i,s,0,0); for(int j=1;j<=m;j++){//每个加工厂 scanf("%d",&x); for(int k=1;k<=n;k++){//订单顺序 int y=x*k; int z=j*n+k+1; Insert(i,z,1,y);Insert(z,i,0,-y); } } } for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ x=i*n+j+1; Insert(x,t,1,0);Insert(t,x,0,0); } } costflow(); double aans=(double)ans/n; if(T!=0)printf("%.6lf\n",aans); else printf("%.6lf",aans); } return 0; }
四、有上下界的网络流
1.无源汇有上下界的可行流,也就是循环流,思想就是先让每条边有一个等于下界的流量,这样每个点不一定满足流量平衡,假设点i的流入减流出等于A[i],则建一个参量网络,使这个网络中第i个点的流入减流出等于A[i],两个相加就满足流量平衡。
为了建立残量网络,需要给每个节点输入或者输出一些流量,这些流量从哪来呢,就新建源汇点ss和tt,如果A[i]<0,说明原来的网络中i节点的流入量小于流出量,那么需要在残量网络中使i节点的流入量比流出量多|A[i]|,这部分流量从ss获取,从ss向i连一条容量为|A[i]|的边。反之就从i向tt连一条容量为|A[i]|的边。
这时候判断是否存在可行流的条件就是源点为ss,汇点为tt的网络是否满流。如果存在,就可以得到一个可行流。
2.有源汇有上下界可行流。仍然建立ss和tt跑循环流,因为加入了源汇点,所以不能单纯计算循环流的大小了。应该计算从s流入,从t流出的部分。把无源汇时的循环流想象成一个环形的流,那么建一条从t到s的边,流经s到t的部分就等于t到s这条边的流量。
3.有源汇有上下界最大流。可行流求出来的流量不一定最大,所以跑完可行流之后,去掉ss和tt,并且去掉t到s的边,以s和t为源汇点跑一遍最大流,加到答案里即可(相当于收集残余的可行流)
4.有源汇有上下界最小流。跑完可行流之后,在残量网络上找到一条s-t的路径使得去掉这条路径上的流量之后仍然满足流量下限,就可以得到一个更小的流。再理解一下dinic的反向边.反向边的流量增加等价于正向边的的流量减少。因此我们在残量网络上找出t到s的流就相当于减小了s到t的流,因此我们在跑出可行流的残量网络上跑t-s最大流,用可行流的大小减去这一次t-s最大流的大小就是最小流的大小。
学习资料https://www.cnblogs.com/liu-runda/p/6262832.html
1.无源汇有上下界可行流(循环流)
zoj 2314 Reactor Cooling
题意:判断是否存在无源汇满足上下界的网络流,如果存在,就求出一个可行流,输出每个边的流量
解:无源汇有上下界网络流模板

/* 在残量网络上新建s和t跑最大流,每个点要么和s连边,要么和t连边,要么既不和s又不和t连边: 如果残量网络中某个点流入量比流出量多x(也就是初始网络中流出量比流入量多x),连一条该点到t的边,容量为x 如果残量网络中某个点流出量比流入量多x,连一条从s到该点的边,容量为x 如果参量网络中某点流量平衡,就可以不与s或t连边(连边也可以,但没必要) */ #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #define maxn 2010 #define maxm 100010 #define INF 0x7f7f7f7f using namespace std; struct node{ int to,pre,w,id; }e[maxm]; int head[maxn],num=1,n,m,s,t,low[maxm],cur[maxn],ans[maxm]; int totflow[maxn],lev[maxn]; void Insert(int from,int to,int w,int id){ e[++num].to=to; e[num].w=w; e[num].id=id; e[num].pre=head[from]; head[from]=num; } bool bfs(){ for(int i=s;i<=t;i++)lev[i]=-1,cur[i]=head[i]; lev[s]=0; queue<int>q; q.push(s); while(!q.empty()){ int now=q.front();q.pop(); for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].w>0&&lev[to]==-1){ lev[to]=lev[now]+1; q.push(to); if(to==t)return 1; } } } return lev[t]!=-1; } int dfs(int now,int flow){ int rest=0,delta; if(now==t)return flow; for(int &i=cur[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].w>0&&lev[to]==lev[now]+1){ delta=dfs(to,min(flow-rest,e[i].w)); rest+=delta; e[i].w-=delta; e[i^1].w+=delta; if(rest==flow)break; } } if(rest<flow)lev[now]=-1; return rest; } int dinic(){ int ans=0,x; while(bfs()){ while(x=dfs(s,INF))ans+=x; } return ans; } void work(){ s=1,t=n+2; num=1; memset(head,0,sizeof(head)); memset(totflow,0,sizeof(totflow)); int x,y,b; for(int i=1;i<=m;i++){ scanf("%d%d%d%d",&x,&y,&low[i],&b); x++;y++; Insert(x,y,b-low[i],i); totflow[x]-=low[i];//totflow为初始流中的流入量-流出量 Insert(y,x,0,i); totflow[y]+=low[i]; } int sum=0; for(int i=2;i<=n+1;i++){ if(totflow[i]<0){ Insert(i,t,-totflow[i],0); Insert(t,i,0,0); } else { sum+=totflow[i];//sum为最大流 Insert(s,i,totflow[i],0); Insert(i,s,0,0); } } if(dinic()==sum){ puts("YES"); for(int i=2;i<=n+1;i++){ for(int j=head[i];j;j=e[j].pre){ if(e[j].id==0||j%2==0)continue; ans[e[j].id]=e[j].w+low[e[j].id]; } } for(int i=1;i<=m;i++)printf("%d\n",ans[i]); } else puts("NO"); } int main(){ int T;scanf("%d",&T); while(T--){ scanf("%d%d",&n,&m); work(); if(T)puts(""); } return 0; }
2.有源汇有上下界可行流
3.有源汇有上下界最大流
zoj 3229 Shoot the Bullet
题意:用n天来给m个妹子拍照,第x个妹子总共最少拍Gx张照片,第i天给特定的Gi个妹子拍照,其中第j个妹子拍照的区间为$[L_{j},R_{j}]$,而且每天拍照的数目有个上限,求一求最多能拍几张照片,或者根本不能完成任务。
解:有源汇有上下界最大流,首先建图,源点为s,汇点为t,中间有n个点表示n天,m个点表示m个妹子;第x个妹子总共最少拍Gx张照片,所以每个妹子向汇点连边,容量上界为INF,下界为Gx;第i天最多拍Bi张照片,所以s向每天连边,边的上界为Bi,下界为0;第i天给第j个妹子拍照,数量必须在$[L_{ij},R_{ij}]$之间,所以第i天向第j个妹子连边,上界为$R_{ij}$,下界为$L_{ij}$。
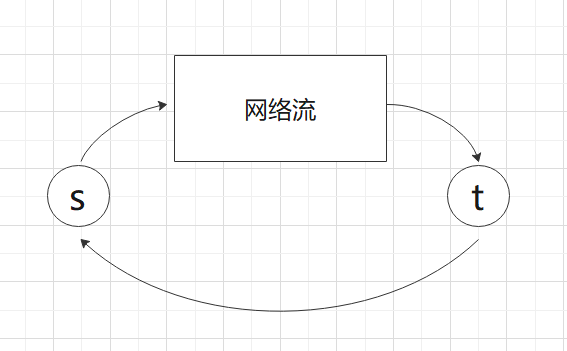
建好图之后由于要跑有源汇的上下界网络流,所以要把t到s连一条下界为0,上界为INF的边,然后新建源汇点ss,tt,跑一下上下界网络流即可,求出来的最大流就是t和s之间边的容量。就体现为下面这个图,由流量平衡可知,有意义的那段网络流的大小就等于t到s的流量。
但由于这样t到s的流量只是一个可行流,不一定最大,这时候只需要将ss和tt删掉,并且删掉t到s的边,在残量网络上再跑一边最大流,答案加上它即可。

#include<iostream> #include<cstdio> #include<queue> #include<cstring> #define maxn 4010 #define maxm 200010 #define INF 0x7f7f7f7f using namespace std; struct node{ int to,pre,w,id; }e[maxm]; int num=1,head[maxn],cur[maxn],totflow[maxn],low[maxm]; int lev[maxn],n,m,s,t,ss,tt,ans[maxm],tot; void Insert(int from,int to,int w,int id){ e[++num].to=to; e[num].w=w; e[num].id=id; e[num].pre=head[from]; head[from]=num; } void Add(int from,int to,int low,int high,int id){ totflow[from]-=low;//totflow[x]:节点x的流入量-流出量 totflow[to]+=low; Insert(from,to,high-low,id); Insert(to,from,0,id); } queue<int>q; bool bfs(){ memset(lev,-1,sizeof(lev)); memcpy(cur,head,sizeof(head)); lev[ss]=0; while(!q.empty())q.pop(); q.push(ss); while(!q.empty()){ int now=q.front();q.pop(); for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].w>0&&lev[to]==-1){ lev[to]=lev[now]+1; // if(to==tt)return 1; q.push(to); } } } return lev[tt]!=-1; } int dfs(int now,int flow){ int rest=0,delta; if(now==tt)return flow; for(int &i=cur[now];i;i=e[i].pre){ int to=e[i].to; if(lev[to]==lev[now]+1&&e[i].w>0){ delta=dfs(to,min(flow-rest,e[i].w)); e[i].w-=delta; e[i^1].w+=delta; rest+=delta; if(rest==flow)break; } } if(rest<flow)lev[now]=-1; return rest; } int dinic(){ int ans=0,x; while(bfs()){ // while(x=dfs(ss,INF)) ans+=dfs(ss,INF); } return ans; } void bound_flow(){ int sum=0; for(int i=s;i<=t;i++){ if(totflow[i]<0){ Insert(i,tt,-totflow[i],0); Insert(tt,i,0,0); } else { sum+=totflow[i]; Insert(ss,i,totflow[i],0); Insert(i,ss,0,0); } } Insert(t,s,INF,0);Insert(s,t,0,0); if(dinic()==sum){ for(int i=head[ss];i;i=e[i].pre) e[i].w=e[i^1].w=0; for(int i=head[tt];i;i=e[i].pre) e[i].w=e[i^1].w=0; int flow0=e[num].w; e[num].w=e[num-1].w=0; // cout<<flow0<<' '<<dinic()<<' '<<endl; ss=s;tt=t; printf("%d\n",flow0+dinic()); for(int i=1;i<=m;i++){ for(int j=head[i+n+1];j;j=e[j].pre){ if(e[j].id!=0){ ans[e[j].id]=e[j].w+low[e[j].id]; } } } for(int i=1;i<=tot;i++) printf("%d\n",ans[i]); } else { puts("-1"); } } void solve(){ s=1;t=n+m+2; ss=n+m+3;tt=n+m+4; num=1; memset(head,0,sizeof(head)); memset(totflow,0,sizeof(totflow)); int x,y; for(int i=1;i<=m;i++){ scanf("%d",&x); Add(n+i+1,t,x,INF,0);//建从n+i+1到t,容量下限为x,上限为INF的边 } int l,h; tot=0; for(int i=1;i<=n;i++){ scanf("%d%d",&x,&y); Add(s,i+1,0,y,0); for(int j=1;j<=x;j++){ tot++; scanf("%d%d%d",&y,&l,&h); Add(i+1,n+y+2,l,h,tot); low[tot]=l; } } bound_flow(); } int main(){ while(scanf("%d%d",&n,&m)!=EOF){ solve(); puts(""); } return 0; }
4.有源汇有上下界最小流
五、分数规划
1.loj 2003 新生舞会
题意:有n个男生和n个女生参加聚会,第i个男生和第j个女生一起跳舞的喜悦程度为$a_{ij}$,不协调程度为$b_{ij}$,假设每对舞伴的喜悦程度为$a_{1},a_{2},...,a_{n}$,每对舞伴的不协调程度为$b_{1},b_{2},...,b_{n}$,令$C=\frac{a_{1}+a_{2}+...+a_{n}}{b_{1}+b_{2}+...+b_{n}}$,求最大的C值。
解:01分数规划,二分答案k,判断是否存在方案使$\frac{a_{1}+a_{2}+...+a_{n}}{b_{1}+b_{2}+...+b_{n}} \geq k$,即$(a_{1}-k*b_{1})+(a_{2}-k*b_{2})+...+(a_{n}-k*b_{n}) \geq 0$,就可以直接跑费用流了。

#include<iostream> #include<cstdio> #include<cstring> #include<queue> #define eps 0.0000001 #define INF 1e9 #define maxn 310 using namespace std; int n,a[maxn][maxn],b[maxn][maxn],num=1,head[maxn],s,t; double dis[maxn],ans; bool vis[maxn]; struct node{ int to,pre,c; double cc; }e[maxn*maxn*2]; void Insert(int from,int to,int c,double cc){ e[++num].to=to; e[num].pre=head[from]; e[num].c=c; e[num].cc=cc; head[from]=num; } bool spfa(){ deque<int>q;q.push_front(s); memset(vis,0,sizeof(vis));vis[s]=1; for(int i=s;i<=t;i++)dis[i]=-INF; dis[s]=0; while(!q.empty()){ int now=q.front();q.pop_front();vis[now]=0; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(e[i].c>0&&dis[to]<dis[now]+e[i].cc){ dis[to]=dis[now]+e[i].cc; if(!vis[to]){ if(!q.empty()&&dis[to]>dis[q.front()])q.push_front(to); else q.push_back(to); vis[to]=1; } } } } return dis[t]>-INF; } int dfs(int now,int flow){ int rest=0,delta; if(now==t){vis[t]=1;return flow;} vis[now]=1; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(!vis[to]&&dis[to]==dis[now]+e[i].cc&&e[i].c>0){ delta=dfs(to,min(flow-rest,e[i].c)); rest+=delta; e[i].c-=delta; e[i^1].c+=delta; ans+=e[i].cc*delta; if(flow==rest)break; } } return rest; } double dinic(){ ans=0; while(spfa()){ vis[t]=1; while(vis[t]){ memset(vis,0,sizeof(vis)); dfs(s,INF); } } return ans; } bool check(double k){ s=1,t=n+n+2; num=1; memset(head,0,sizeof(head)); for(int i=1;i<=n;i++){ Insert(s,i+1,1,0);Insert(i+1,s,0,0); Insert(i+n+1,t,1,0);Insert(t,i+n+1,0,0); for(int j=1;j<=n;j++){ double w=(double)a[i][j]-k*b[i][j]; Insert(i+1,j+n+1,1,w);Insert(j+n+1,i+1,0,-w); } } if(dinic()>=0)return 1; else return 0; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&a[i][j]); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&b[i][j]); double l=0,r=20000; while(r-l>eps){ double mid=(l+r)/2.0; if(check(mid))l=mid; else r=mid; } printf("%.6lf\n",l); return 0; }
2.loj 2214 方伯伯运椰子
题意:一共有n+2个节点,起点为n+1,终点为n+2,共m条边,边的参数为(x,y,a,b,c,d),表示从x到y有一条有向边,容量减少一个单位的费用为a,增大一个单位的费用为b,初始容量为c,单位费用为d。初始状态下每条边都满流,满足流量平衡,此时总费用为X,将一些边扩大或缩小,并保证每条边仍然满流且最大流不能比原来小,此时费用为Y,假设一共进行了k次调整,求(X-Y)/k的最大值
解:显然最大流不变时最优。从x到y连一条权值为b+d的边,表示容量扩大一次的费用;从y到x连一条权值为a-d的边代表容量缩小一次的费用,该边仅当c>0时存在。
假如这样建立的图中存在一个负环,那么修改流量的时候沿这个环绕一圈,答案一定是最优,而且因为容量限制,这个环不能无限绕,所以是合法的。这样做正确的原因是,原来这个环就流量平衡,将环上所有的边同时加或者减相应容量,仍然流量平衡。
设当前二分的答案为ans,那么(X-Y)/k>=ans,即Y+k*ans<=x,由于题目保证ans>0,所以需要找到一个更优的网络,使它的费用最小。此时将ans加在每条边上,找一下图中是否存在负环,就可以知道在这个答案下是否存在可优化的网络。

#include<iostream> #include<cstdio> #include<queue> #include<cstring> #define maxn 5010 #define eps 0.0000001 using namespace std; int n,m,head[maxn],num,cnt[maxn]; double dis[maxn]; bool vis[maxn]; struct node{ int to,pre,v; }e[maxn*2]; void Insert(int from,int to,int v){ e[++num].to=to; e[num].pre=head[from]; e[num].v=v; head[from]=num; } bool spfa(double x){ memset(vis,0,sizeof(vis)); memset(dis,0x7f,sizeof(dis)); memset(cnt,0,sizeof(cnt)); deque<int>q;q.push_front(n+1); vis[n+1]=1;cnt[n+1]=1;dis[n+1]=0; while(!q.empty()){ int now=q.front();q.pop_front(); vis[now]=0; if(cnt[now]>n+2)return 1; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; double len=e[i].v+x; if(dis[to]>dis[now]+len){ dis[to]=dis[now]+len; if(!vis[to]){ vis[to]=1; cnt[to]++; if(!q.empty()&&dis[to]<dis[q.front()])q.push_front(to); else q.push_back(to); } } } } return 0; } int main(){ scanf("%d%d",&n,&m); int x,y,a,b,c,d; double l=0,r; for(int i=1;i<=m;i++){ scanf("%d%d%d%d%d%d",&x,&y,&a,&b,&c,&d); Insert(x,y,b+d); if(c>0)Insert(y,x,a-d); if(a-d<0)r+=d-a; } double ans; while(r-l>eps){ double mid=(l+r)/2.0; if(spfa(mid))ans=mid,l=mid; else r=mid; } printf("%.2lf",ans); return 0; }
六、习题
1.[NOI 2008]志愿者招募
题意:申奥成功后,布布经过不懈努力,终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难题:为即将启动的奥运新项目招募一批短期志愿者。经过估算,这个项目需要N 天才能完成,其中第i 天至少需要Ai 个人。 布布通过了解得知,一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天,招募费用是每人Ci 元。新官上任三把火,为了出色地完成自己的工作,布布希望用尽量少的费用招募足够的志愿者,但这并不是他的特长!于是布布找到了你,希望你帮他设计一种最优的招募方案(只需要找出最少费用)。
解:


