2020-07-03 牛客编程挑战
昨天多校训练在牛客组队,看到有个一战到底编程挑战,有些好奇就进去看看,做出来俩,都是模拟,第三个是动态规划,看了看没思路就走了,4号早晨起来补了一下。
(有几个latex公式我暂时不太会搞,写出来可能看着有点蠢,见谅)
1.简单题(重要极限+快速幂)
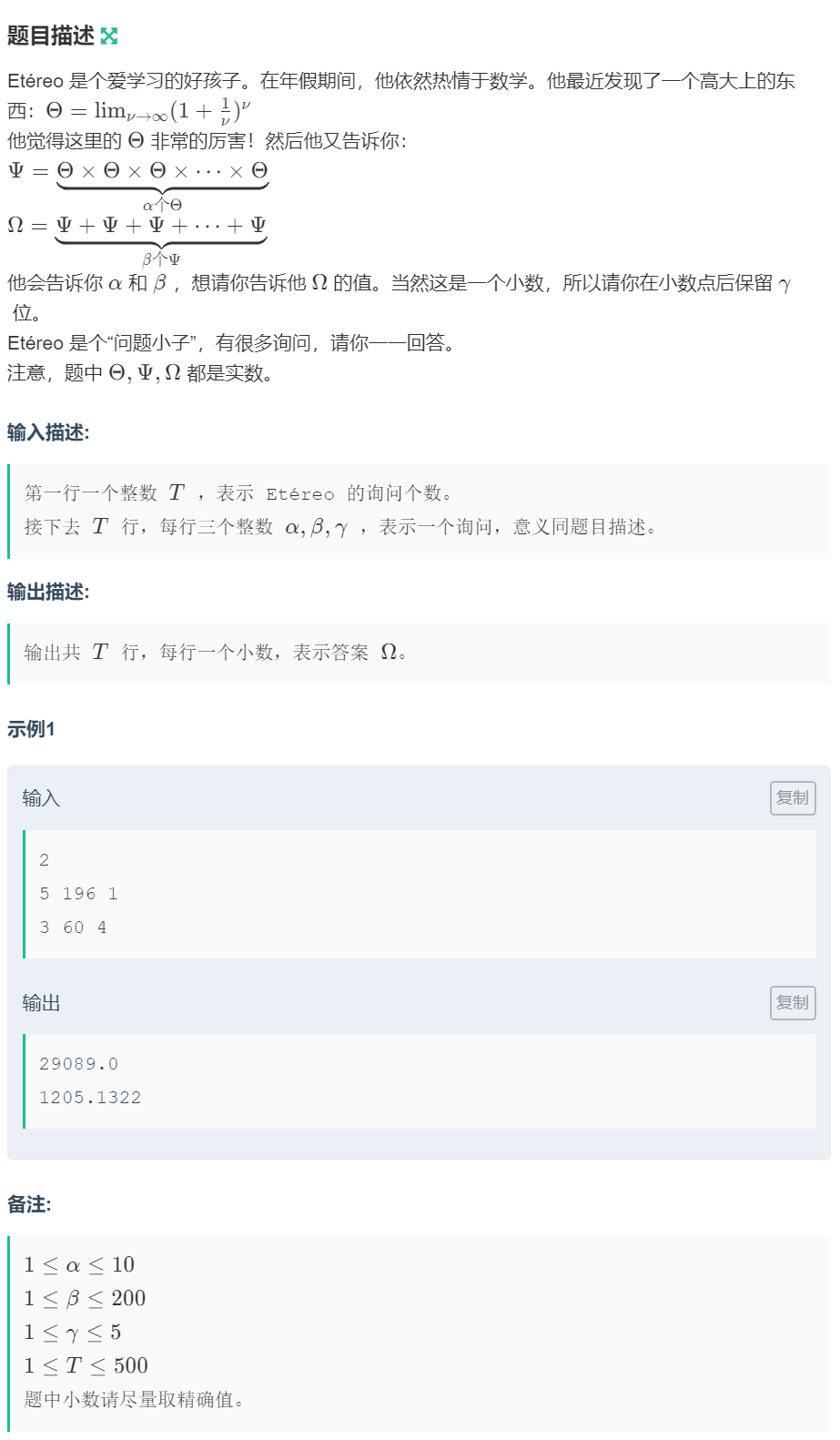
解:题目中的O就是常见的重要极限$lim_{x\to \infty}(1+\frac{1}{x})^x = e$,e的值是从math.h直接拿过来的,精度挺可以的,拿来直接快速幂就好了,后面保留小数那里我写的有点蠢,用cout的格式化输出会更好一些。
#include<iostream> #include<cstdio> #include<cmath> using namespace std; double Pow(double x,int y){ double res=1; while(y){ if(y&1)res=res*x; x=x*x; y>>=1; } return res; } int main(){ int T; scanf("%d",&T); while(T--){ int x,y,z; scanf("%d%d%d",&x,&y,&z); double ans=(double)y*Pow(M_E,x); if(z==1)printf("%.1f\n",ans); if(z==2)printf("%.2f\n",ans); if(z==3)printf("%.3f\n",ans); if(z==4)printf("%.4f\n",ans); if(z==5)printf("%.5f\n",ans); } return 0; }
2.消息列表(模拟)
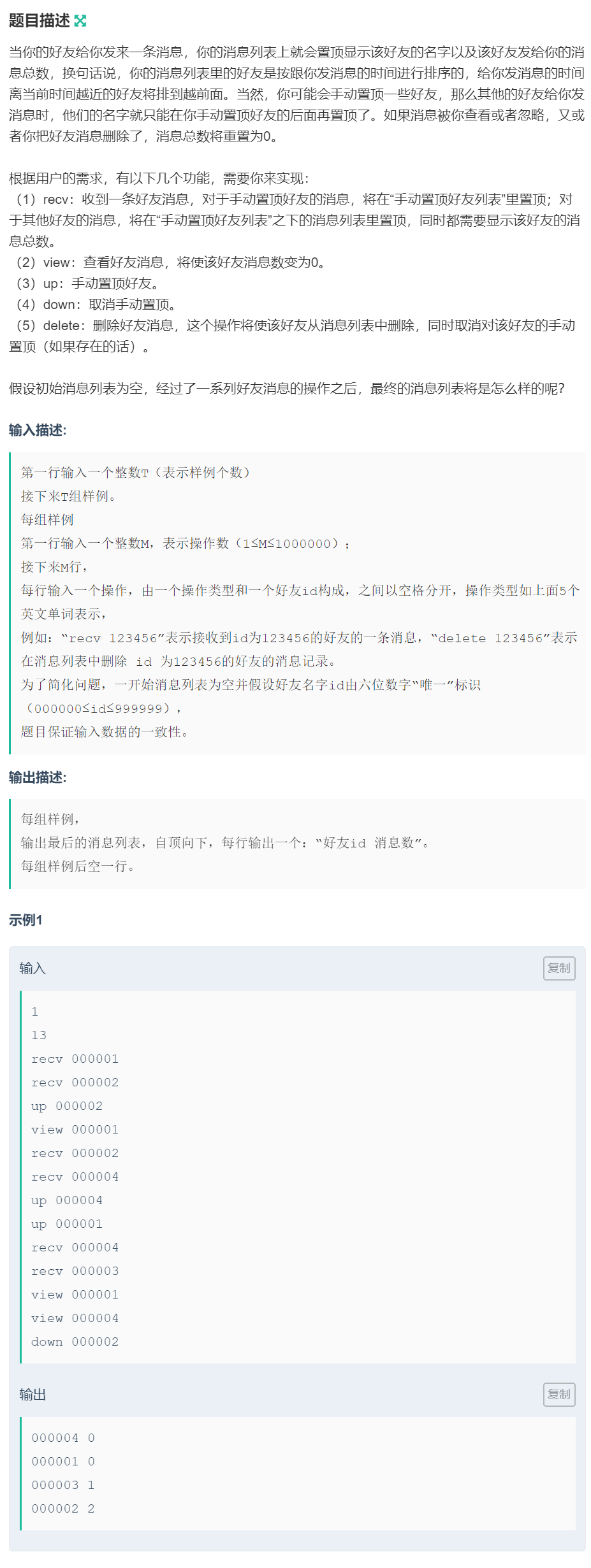
解:这个题也没什么难度,我思路就是拿一个结构体存储每个人的信息(这个人的编号,消息总条数,是否置顶,最后一次发消息的时间),这样再用一个map,把所有人标记到,避免重复加入结构体。这样的话,最后只要将结构体排序就可以了,但是被卡住了空间,只能用vector,或者用牛客的自测调试多试几次,卡着空间限制应该也能过,不然的话vector也没法过是吧。
#include<iostream> #include<cstdio> #include<cstring> #include<map> #include<vector> #include<algorithm> #define maxn 1000001 #define INF 1000000 using namespace std; struct node{ string s; int last; int tot; }; vector<node>q; map<string,int>p; int T,n,cnt; char s1[10]; string s2; bool cmp(node u,node v){ if(u.last!=v.last)return u.last>v.last; } int main(){ scanf("%d",&T); while(T--){ scanf("%d",&n); cnt=0; vector<node>().swap(q); p.clear(); for(int i=1;i<=n;i++){ scanf("%s",s1); cin>>s2; if(!p[s2]){ node a; cnt++; p[s2]=cnt; a.s=s2; a.last=0; a.tot=0; q.push_back(a); } int now=p[s2]-1; if(s1[0]=='r'){ if(q[now].last>=INF)q[now].last=i+INF; else q[now].last=i; q[now].tot++; } else if(s1[0]=='v'){ q[now].tot=0; } else if(s1[0]=='u'){ if(q[now].last<INF)q[now].last+=INF; } else if(s1[1]=='o'){ if(q[now].last>=INF)q[now].last-=INF; } else if(s1[1]=='e'){ q[now].tot=0; q[now].last=0; } } sort(q.begin(),q.end(),cmp); // cout<<cnt<<endl; for(int i=0;i<cnt;i++){ if(q[i].last==0)break; cout<<q[i].s<<" "; printf("%d\n",q[i].tot); } puts(""); } return 0; }
3.陨石的秘密(动态规划)

解:一道动态规划的题目。对于这些变量,设f[i][j][k][d]表示串中有i个()、j个[]、k个{}、深度不大于d时的方案总数。由定义可知,两个SS串拼在一起也是一个SS串,我们可以借此来进行动态规划。但是,若一个SS串为ABC,在计算时就会将AB+C和A+BC作为两个方案计算在内,但实际上是同一种方案。因此,为了避免重复,可以在动态规划时令一个串强制在最外面加上一个括号(满足要求的最小括号)。所以,首先枚举一个串中有的每种括号的数量,然后把所有括号分成两部分,对答案的贡献即为分成的两个串的乘积。注意取模。
#include<iostream> #include<cstdio> #define mod 11380 using namespace std; int n,l1,l2,l3,D,f[11][11][11][31]; int main(){ scanf("%d%d%d%d",&l1,&l2,&l3,&D); f[0][0][0][0]=1; for(int i=0;i<=l1;i++){ for(int j=0;j<=l2;j++){ for(int k=0;k<=l3;k++){ for(int l=1;l<=D;l++){ if(i!=0||j!=0||k!=0){ int tmp=0; for(int a=0;a<k;a++){ tmp=(tmp+f[i][j][k-a-1][l]*f[0][0][a][l-1])%mod; } for(int b=0;b<j;b++){ for(int a=0;a<=k;a++) tmp=(tmp+f[i][j-b-1][k-a][l]*f[0][b][a][l-1])%mod; } for(int c=0;c<i;c++){ for(int b=0;b<=j;b++){ for(int a=0;a<=k;a++){ tmp=(tmp+f[i-c-1][j-b][k-a][l]*f[c][b][a][l-1])%mod; } } } f[i][j][k][l]=tmp; } else f[i][j][k][l]=1; } } } } int ans=((f[l1][l2][l3][D]-f[l1][l2][l3][D-1])%mod+mod)%mod; printf("%d\n",ans); return 0; }
