2021/3/17算法题打卡
斐波那契变题
标题:斐波那契
斐波那契数列大家都非常熟悉。它的定义是:
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x>2)对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式参见【图1.png】但这个数字依然很大,所以需要再对 p 求模。
【数据格式】
输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)
输出为1个整数例如,如果输入:
2 3 5
程序应该输出:
0再例如,输入:
15 11 29
程序应该输出:
25资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
方法一:
解析:
f(x) = f(x-1)+f(x-2)-->f(x+1)=f(x)+f(x-1)-->f(x+1)-f(x-1)
Σf(n) = f(n+2)-1
原题目等价于:(f(n+2)-1)%f(m)%p --> m>=n+2,余f(m)无意义
-->(f(n+2)-1)%p
(f(n+2)-1)%f(m)%p --> m<n+2
40分
代码:
public class T9斐波那契 {
static int n;
static int m;
static int p;
static Long[] longs;
private static BigInteger fib(int k) {
for(int i=3;i<=k;i++){
longs[i]=longs[i-1]+longs[i-2];
}
return BigInteger.valueOf(longs[k]);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
p = scanner.nextInt();
longs = new Long[n+3];
longs[1]=Long.valueOf(1);
longs[2]=Long.valueOf(1);
BigInteger sum=fib(n+2);
if(m>=n+2) {
sum = sum.subtract(BigInteger.ONE);
sum = sum.mod(BigInteger.valueOf(p));
System.out.println(sum);
}else{
BigInteger numB = BigInteger.valueOf(longs[m]);
sum = sum.mod(numB);
sum = sum.mod(BigInteger.valueOf(p));
sum = sum.subtract(BigInteger.ONE);
}
System.out.println(sum);
}
}
但是本方法对于10^18次方的数据来说,一是超时,二是long无法存下这么大的数据,所以最终只能得40分
方法二:
解析
可以通过矩阵快速幂来得到结果,这是最快的解法 O(logn),用该方法可以解决超时问题
矩阵解法:
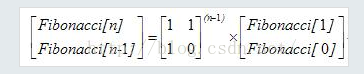
60分
代码:
public class T9斐波那契2 {
static long n;
static long m;
static long p;
//矩阵相乘
public static M mul(M m1,M m2){
M ans = new M();
ans.data[0][0]=m1.data[0][0]*m2.data[0][0]+m1.data[0][1]*m2.data[1][0];
ans.data[0][1]=m1.data[0][0]*m2.data[0][1]+m1.data[0][1]*m2.data[1][1];
ans.data[1][0]=m1.data[1][0]*m2.data[0][0]+m1.data[1][1]*m2.data[1][0];
ans.data[1][1]=m1.data[1][0]*m2.data[0][1]+m1.data[1][1]*m2.data[1][1];
return ans;
}
//矩阵相乘
public static M mul(M m1,M m2,long mod){
M ans = new M();
ans.data[0][0]=((m1.data[0][0]*m2.data[0][0])%mod+(m1.data[0][1]*m2.data[1][0])%mod)%mod;
ans.data[0][1]=((m1.data[0][0]*m2.data[0][1])%mod+(m1.data[0][1]*m2.data[1][1])%mod)%mod;
ans.data[1][0]=((m1.data[1][0]*m2.data[0][0])%mod+(m1.data[1][1]*m2.data[1][0])%mod)%mod;
ans.data[1][1]=((m1.data[1][0]*m2.data[0][1])%mod+(m1.data[1][1]*m2.data[1][1])%mod)%mod;
return ans;
}
//m的m次幂
public static M mPow(M m,long n){
M E = new M();//单位矩阵
E.data[0][0]=1;
E.data[0][1]=0;
E.data[1][1]=1;
E.data[1][0]=0;
while(n!=0){
if((n&1)==1){
E = mul(E,m);
}
m=mul(m,m);
n>>=1;
}
return E;
}
//m的m次幂
public static M mPow(M m,long n,long mod){
M E = new M();//单位矩阵
E.data[0][0]=1;
E.data[0][1]=0;
E.data[1][1]=1;
E.data[1][0]=0;
while(n!=0){
if((n&1)==1){
E = mul(E,m,mod);
}
m=mul(m,m,mod);
n>>=1;
}
return E;
}
public static long fib(long i){
//[1,1]B^(i-2)
M A = new M();
A.data[0][0]=1;
A.data[0][1]=1;
A.data[1][0]=0;
A.data[1][1]=0;
M B = new M();
B.data[0][0]=1;
B.data[0][1]=1;
B.data[1][0]=1;
B.data[1][1]=0;
M ans = mul(A,mPow(B,i-2));
return ans.data[0][0];
}
public static long fib(long i,long mod){
//[1,1]B^(i-2)
M A = new M();
A.data[0][0]=1;
A.data[0][1]=1;
A.data[1][0]=0;
A.data[1][1]=0;
M B = new M();
B.data[0][0]=1;
B.data[0][1]=1;
B.data[1][0]=1;
B.data[1][1]=0;
M ans = mul(A,mPow(B,i-2,mod),mod);
return ans.data[0][0];
}
static void solve(){
if(m>=n+2){
System.out.println(fib(n+2,p)-1);
}else{
System.out.println((fib(n+2,fib(m))-1)%p);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextLong();
m = scanner.nextLong();
p = scanner.nextLong();
solve();
}
static class M{
long data[][] = new long[2][2];
}
}
方法三
解析
整数快速运算,并在乘法中加入模运算
100分
代码
//如果 m>=n+2那么f(m)>Σf(n),结果是(f(n+2)-1)%p
//否则 结果为(f(n+2)-1)%f(m)%p==f(n+2)%f(m)%p-1
public class _09_斐波那契 {
public static void main(String[] args) {
// for (int i = 3; i <=10 ; i++) {
// System.out.println(fib(i).longValue());
// }
Scanner sc = new Scanner(System.in);
long n, m, p;
n = sc.nextLong();
m = sc.nextLong();
p = sc.nextLong();
BigInteger bigP = BigInteger.valueOf(p);
if (m >= n + 2) {
BigInteger ans = fib(n + 2, bigP);
System.out.println(ans.mod(bigP).longValue() - 1);
} else {
BigInteger fibm = fib(m);
BigInteger ans = fib(n + 2, fibm);
System.out.println(ans.mod(fibm).mod(bigP).longValue() - 1);
}
}
/*快速矩阵求fib*/
private static BigInteger fib(long m) {
BigInteger[][] ans = mPow(m - 2);
return ans[0][0].add(ans[1][0]);
}
private static BigInteger fib(long m,BigInteger mod) {
BigInteger[][] ans = mPow(m - 2,mod);
return ans[0][0].add(ans[1][0]);
}
/*矩阵快速幂运算*/
private static BigInteger[][] mPow(long n) {
// a 1110
BigInteger[][] a =
{
{
BigInteger.ONE, BigInteger.ONE
},
{
BigInteger.ONE, BigInteger.ZERO
}
};
//单元矩阵
BigInteger[][] ans =
{
{
BigInteger.ONE, BigInteger.ZERO
},
{
BigInteger.ZERO, BigInteger.ONE
}
};
while (n != 0) {
if ((n & 1) == 1) {
//结果ans乘以当前平方
BigInteger t1=ans[0][0];
BigInteger t2=ans[1][0];
ans[0][0] = ans[0][0].multiply(a[0][0]).add(ans[0][1].multiply(a[1][0]));
ans[0][1] = t1.multiply(a[0][1]).add(ans[0][1].multiply(a[1][1]));
ans[1][0] = ans[1][0].multiply(a[0][0]).add(ans[1][1].multiply(a[1][0]));
ans[1][1] = t2.multiply(a[0][1]).add(ans[1][1].multiply(a[1][1]));
}
//对a进行平方
BigInteger t1=a[0][0];
BigInteger t2=a[1][0];
BigInteger t3=a[0][1];
a[0][0] = a[0][0].multiply(a[0][0]).add(a[0][1].multiply(a[1][0]));
a[0][1] = t1.multiply(a[0][1]).add(a[0][1].multiply(a[1][1]));
a[1][0] = a[1][0].multiply(t1).add(a[1][1].multiply(a[1][0]));
a[1][1] = t2.multiply(t3).add(a[1][1].multiply(a[1][1]));
n >>= 1;
}
return ans;
}
private static BigInteger[][] mPow(long n,BigInteger mod) {
BigInteger[][] a =
{
{
BigInteger.ONE, BigInteger.ONE
},
{
BigInteger.ONE, BigInteger.ZERO
}
};
//单元矩阵
BigInteger[][] ans =
{
{
BigInteger.ONE, BigInteger.ZERO
},
{
BigInteger.ZERO, BigInteger.ONE
}
};
while (n != 0) {
if ((n & 1) == 1) {
//结果乘以当前平方
BigInteger t1=ans[0][0];
BigInteger t2=ans[1][0];
ans[0][0] = ans[0][0].multiply(a[0][0]).add(ans[0][1].multiply(a[1][0])).mod(mod);
ans[0][1] = t1.multiply(a[0][1]).add(ans[0][1].multiply(a[1][1])).mod(mod);
ans[1][0] = ans[1][0].multiply(a[0][0]).add(ans[1][1].multiply(a[1][0])).mod(mod);
ans[1][1] = t2.multiply(a[0][1]).add(ans[1][1].multiply(a[1][1])).mod(mod);
}
//进行平方
BigInteger t1=a[0][0];
BigInteger t2=a[1][0];
BigInteger t3=a[0][1];
a[0][0] = a[0][0].multiply(a[0][0]).add(a[0][1].multiply(a[1][0])).mod(mod);
a[0][1] = t1.multiply(a[0][1]).add(a[0][1].multiply(a[1][1])).mod(mod);
a[1][0] = a[1][0].multiply(t1).add(a[1][1].multiply(a[1][0])).mod(mod);
a[1][1] = t2.multiply(t3).add(a[1][1].multiply(a[1][1])).mod(mod);
n >>= 1;
}
return ans;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号