4.4清北学堂Day1 主要内容:数论,数学
Day 1;
1、常见的高精
- 输入输出都用字符数组;
- 字符数组的实际长度用strlen()来求;
- 运算时倒序运算,把每一个字符都-‘0’
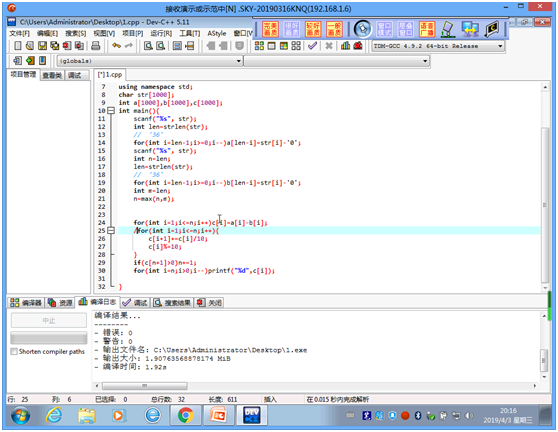
- 进位的处理上也要注意;
- 小数减大数时先判断大小然后加负号

- 只能用while不能用if 因为if只能去掉一个0,while去掉所有的前导零
高精减:
高精乘;
通过逐位相乘,进完位之后输出


2、特殊处理
高精数除以单精数

压位技巧:

把对十取模变成了%10000或者更长,对加和减没啥用,但是乘除的时候能够大量提高速度,复杂度为o(n/m);
在int下可以最多压9位,能够很好的减少时间
2、模意义下运算
模7意义下的运算
模意义下运算这一块比较难,主要还是日后求逆元的时候比较费劲
3*3=2 4+5=2 4-5=6
即3*3 mod 7=2
无除法运算(但可以用逆元来代替)
满足基本的交换律、分配率、结合律
对中间结果取模不影响最终答案 ;
5*5*5 mod 7 = 6
(5*5 mod 7)^5 mod 7 = 4*5 mod 7
快速幂
计算a^b%p=?
暴力O(b)
两种解决思路:
分治
分治代码pow(a,b)%c

快速幂
快速幂代码
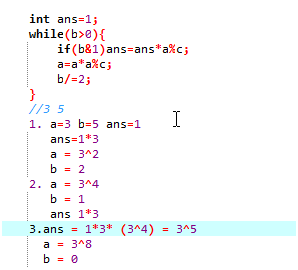
b&1指二进制下b的第一位
费马小定理
t=b*a^(p-1)=b
t=b*1=b
/a=*a^(p-2);
用费马小定理的方法来代替/a;

PS!!!!!
O(1)计算组合数:
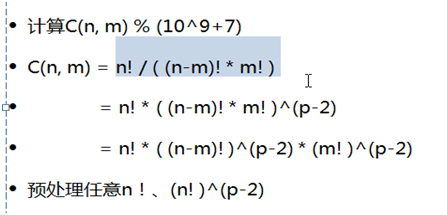
第三步进行了拆分,把两个阶乘拆开了
最后发现组合数只与n!、(n!)^(p-2)
一个很省时间的模板。。。。。。但是不习惯用
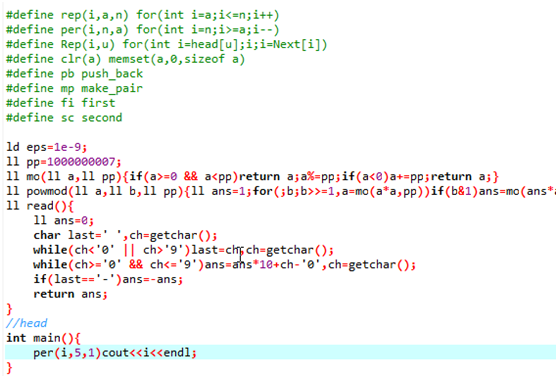
#define clr(a) memset(a,0,sizeof(a))
清零
Ps:快读比scanf快4倍左右
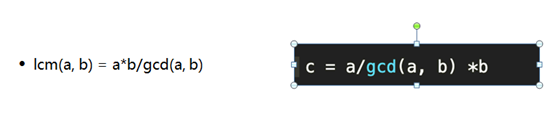
GCD和LCM
没什么可讲的,唯一注意的是用GCD求LCM要注意顺序。。。。前一种有可能会爆
筛素数
弱智筛法就不贴了
下面是埃氏筛
先补一个很有意思的东西
1+1/2+1/3+1/4+....+1/n=log n
线性筛代码

欧拉函数

对于大范围内求质因数个数硬解肯定太慢,用线性筛优化
先用线性筛找到每一个数的最小质因子(rec[i])

分析:第二个if里,当i的指数>=2时就可以直接乘,(主要是看rec[i]对于phi[i]的贡献,例如一次幂二次幂等)当指数>2时,说明i因数分解式当中有多个该质因子,那么我们就可以直接相乘。
例如:
36=2^2*3^2
Phi[36]=phi[18]*2
=2*1*3*2=6;=12
18=2*3^2
Phi[18]=2^(1-1) * (2-1) * 3^(2-1) * (3-1)
=1*1*3*2=6;
否则在(i/rec[i])基础上乘该数最小质因子的欧拉函数(即rec[i]-1)。
例如phi[15]和phi[30]
Phi[15]=(3-1)*(5-1)=8
Phi[30]=(2-1)* (3-1)*(5-1)=8
=phi[30/2]*(2-1)=8
通过对欧拉函数的应用,我们可以慢慢的发现这条定理:
欧拉定理

矩阵
1、
- 一个m×n的矩阵就是m×n个数排成m行n列的一个数阵
- 一个m×p的矩阵A 乘 一个一个p×n的矩阵B 得到一个矩阵一个m×n的矩阵AB
- 其中
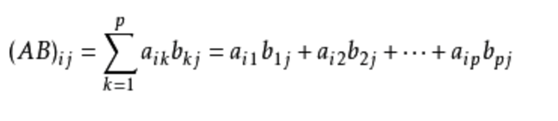
乘法的时候,第i行第j列就等于原本两个矩阵里头前矩阵i行和后矩阵j列全部元素对应相乘
- 注意!矩阵乘法满足结合律、分配率
- 不满足交换律
应用:
求斐波那契数列第k项的值
Fi表示斐波那契第i项
0 1 f1 f2 f2
1 1 f2 f1+f2 f3
0 1 K-1次幂 f1 fk
1 1 f2 fk+1
代码实现

ans起初是单位矩阵
计算f(n) = 4f(n-1) – 3f(n-2) + 2f(n-4) 的第k项
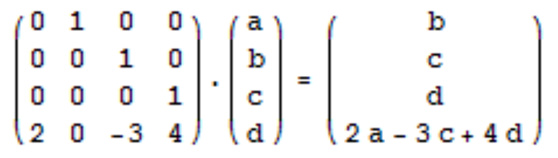
套模板,先找一个矩阵看能不能使得前矩阵通过运算变成后矩阵,可以通过在前(n-1)行用01来求解,最后一行按题目要求的系数填入的方法
邻接矩阵
表示第i行的点能不能到第j个点上
比如
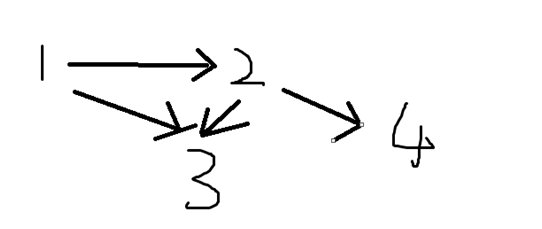
可以得到
0 1 1 0
0 0 1 1
0 0 0 0
0 0 0 0
矩阵的k次幂表示走几步能到达
高斯消元
1、 应用场景:解齐次线性方程组
例:
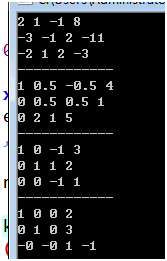
解齐次线性方程
2x + y - z = 8
-3x - y + 2z = -11
-2x + y + 2z = -3
可以得到
2 1 -1 8
-3 -1 2 -11
-2 1 2 -3
常规的高斯消元法只需要循环(或者递归)求解即可
有一个很重要的区别
行列式消元的时候,当a[i][i]==0的时候,对该列进行交换;
矩阵消元的时候,当a[i][i]==0的时候,则i++;
代码实现:
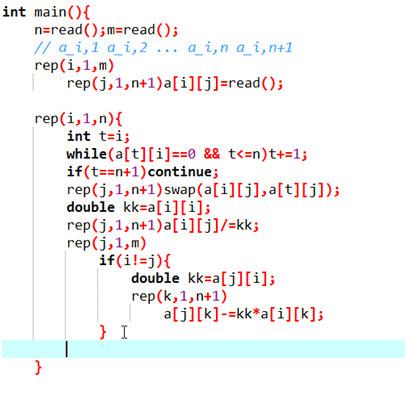
行列式 emmmm其实应该在矩阵前头啊
1.把齐次线性方程组的矩阵拿出来构成一个行列式,若值为0则无解或无穷多解,非0则有解
2.解法:用高斯消元消成上三角就行,或者降阶求解
矩阵逆元:
若矩阵B*A=I则称B为A的左逆元
有逆元的前提:矩阵行列式不为0
求左逆元:对于A矩阵的第二行减去第一行,其实就是对于一个换单位矩阵在单独的某一行进行系数变换
左逆元其实就是高斯消元过程中的矩阵连乘
同理,右逆元是对列进行系数变换
矩阵树定理
- 一个图的邻接矩阵G:对于无向图的边(u,v),G[u][v]++,G[v][u]++
一个图的度数矩阵(有多少条边与之相连,那么他的度数就是多少)D:对于无向图的边(u,v),D[u][u]++,D[v][v]++
- 而通过这两个矩阵就可以构造出图G的基尔霍夫矩阵:C=D-G.
- Matrix Tree定理:将图G的基尔霍夫矩阵去掉第i行和第i列(i可以取任意值,可以证明所得到的结果相同),得到(n-1)*(n-1)的矩阵,对这个矩阵进行行列式的值求解,abs(det(A))即为图G的生成树个数。

